2018年高中数学第2章平面解析几何初步2.3.1空间直角坐标系课件3苏教版必修2(15张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.3.1空间直角坐标系课件3苏教版必修2(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:35:56 | ||
图片预览


文档简介
课件15张PPT。2.3.1 空间直角坐标系平面解析几何的基本思想是什么?借助平面直角坐标系,用代数方法来研究直线、圆等图形的有关性质.那么,怎样用坐标来表示空间任意一点的位置呢?问题情境 建立平面直角坐标系,平面上任意一点与坐标建立一一对应关系.
直线、圆等几何图形就与方程f(x,y)=0建立对应关系,进而利用方程揭
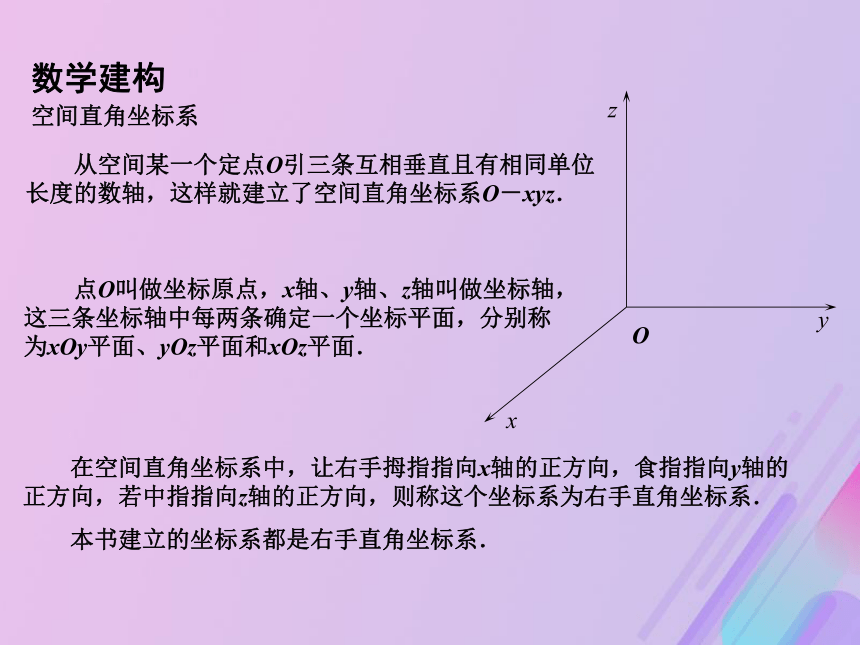
示图形的有关性质.空间直角坐标系xyzO 从空间某一个定点O引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系O-xyz. 点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xOy平面、yOz平面和xOz平面. 在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,若中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
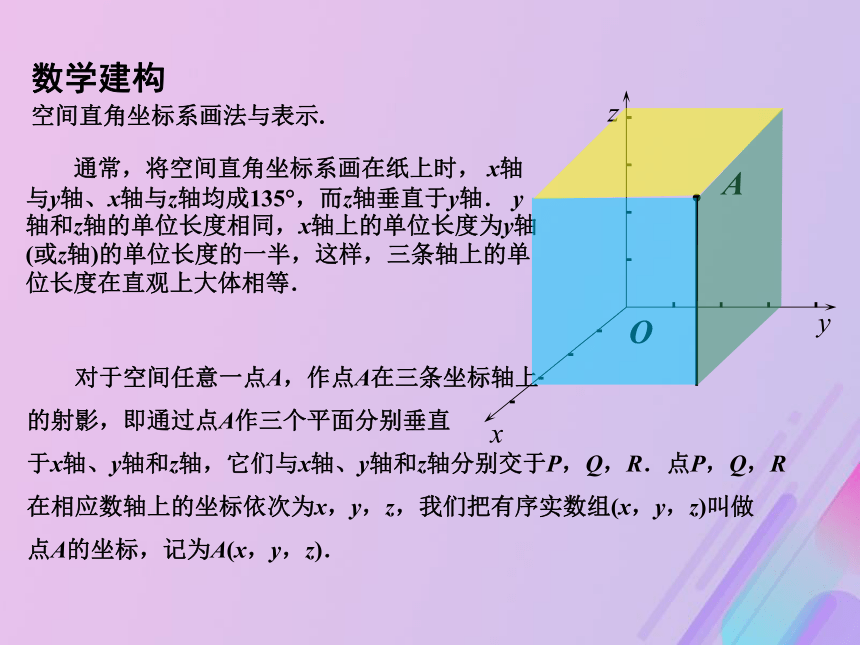
本书建立的坐标系都是右手直角坐标系.数学建构xyzO 通常,将空间直角坐标系画在纸上时, x轴与y轴、x轴与z轴均成135?,而z轴垂直于y轴. y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半,这样,三条轴上的单位长度在直观上大体相等. 对于空间任意一点A,作点A在三条坐标轴上
的射影,即通过点A作三个平面分别垂直
于x轴、y轴和z轴,它们与x轴、y轴和z轴分别交于P,Q,R.点P,Q,R
在相应数轴上的坐标依次为x,y,z,我们把有序实数组(x,y,z)叫做
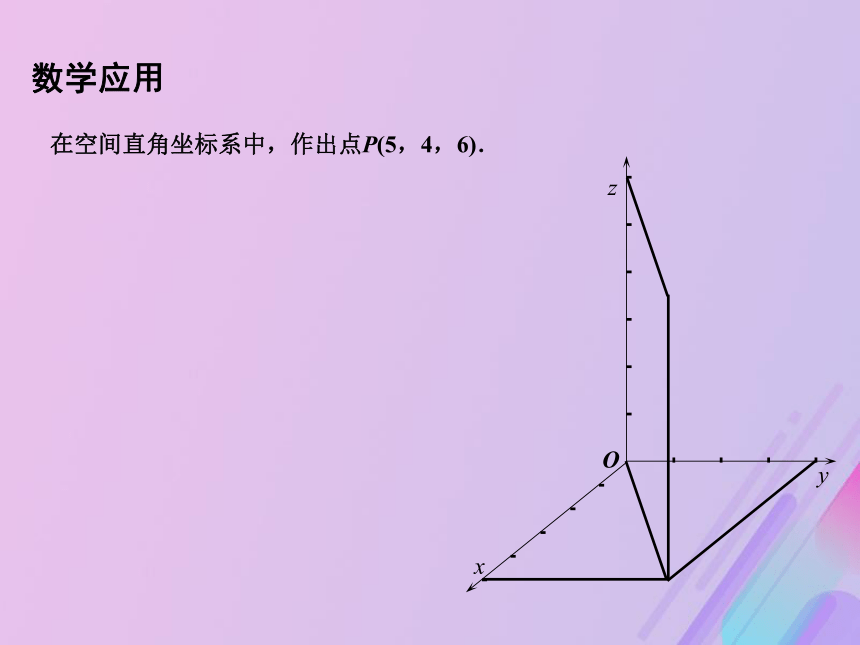
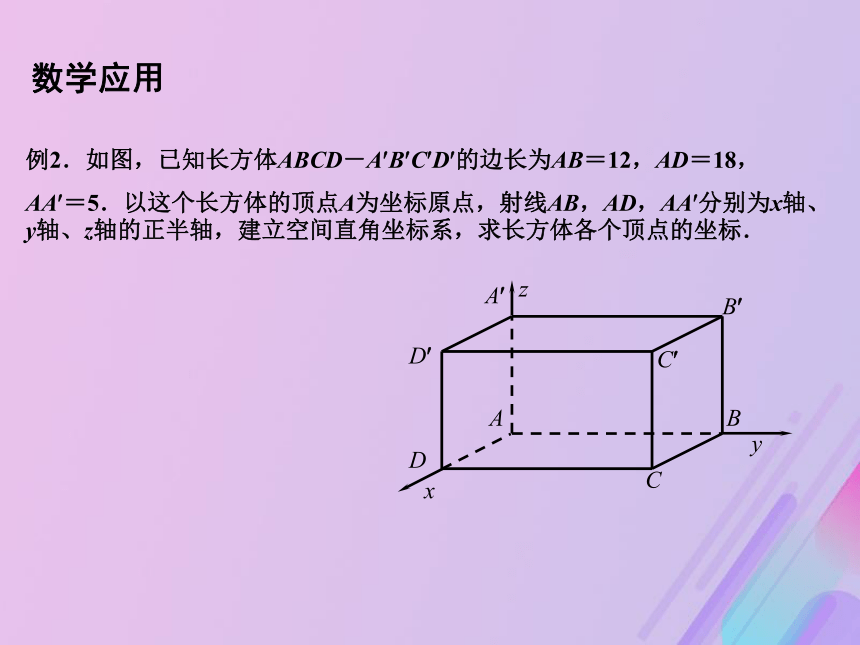
点A的坐标,记为A(x,y,z). A空间直角坐标系画法与表示.数学建构在空间直角坐标系中,作出点P(5,4,6).xyzO数学应用D B CB?A?D?C?A x z y例2.如图,已知长方体ABCD-A?B?C?D?的边长为AB=12,AD=18,
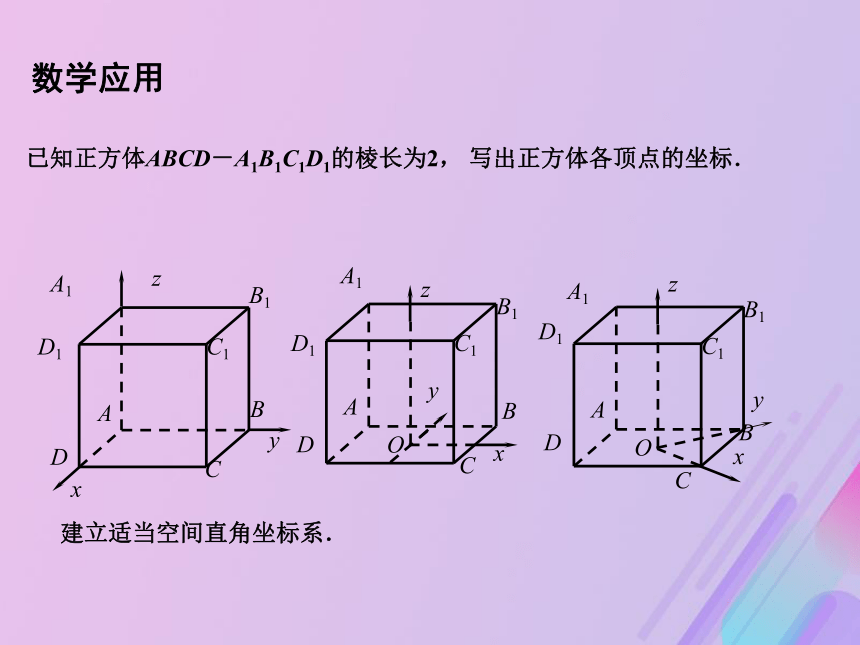
AA?=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA?分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,求长方体各个顶点的坐标. 数学应用B1D B CB1A1D1C1A x z y已知正方体ABCD-A1B1C1D1的棱长为2, 写出正方体各顶点的坐标.建立适当空间直角坐标系.数学应用13zxyO 在正四棱锥S-ABCD中,建立如图所示的空间直角坐标系,根据条件,确定各顶点的坐标.SABCD数学应用点P(3,-2,1)关于坐标平面xOy的对称点的坐标为_________________;
点Q(-2,-3,1)关于原点的对称点的坐标为_________________;
点R(2,4,1)关于z轴的对称点的坐标为_____________________.P?(3,-2,-1)Q?(2,3,-1)R?(- 2,- 4,1)数学应用点P(x,y,z)关于
原点的对称点的坐标为______________________;
坐标平面xOy的对称点的坐标为_______________;
坐标平面yOz的对称点的坐标为_______________;
x轴的对称点的坐标为________________________;
z轴的对称点的坐标为________________________.P1(-x,-y,-z)空间任一点P(x,y,z)关于原点、轴、坐标平面的对称点的坐标特征.P2(x,y,-z)P5(-x,-y,z)P3(-x ,y,z)P4(x,-y,-z)数学建构1.下列点中,位于yoz平面内的是( )
A.(2,2,0) B.(0,2,2)
C.(2,0,2) D.(2,0,0)
2.点P(4,2,6)在xOy平面内射影P?的坐标是________.
3.点P(-2,-1,4)到xOz平面的距离是____________.B(4,2,0)1数学应用平面xOy内点的坐标特征为________________;
平面yOz内点的坐标特征为________________;
平面xOz内点的坐标特征为________________;
x轴上点的坐标特征为_____________________;
y轴上点的坐标特征为_____________________;
z轴上点的坐标特征为_____________________.空间内落在坐标轴上或坐标平面内的点的坐标特征. z=0 x=0 y=0 y=0,且z=0 x=0,且z=0 x=0,且y=0数学建构例3.(1)在空间直角坐标系O-xyz中,画出不共线的3个点P,Q,R,使得这3个点的坐标都满足z=3,并画出图形;
(2)写出由这三个点确定的平面内的点的坐标应满足的条件. xyzO数学应用 如图,已知四棱锥P-ABCD中,PA垂直于矩形ABCD所在平面,M是PC的中点,N在PB上,且PN=3NB,已知AB=4,AD=3,PA=5, 建立如图所示坐标系,写出点P,A,B,C,D,M,N的坐标.xyzAPBDCMN数学应用1.右手坐标系的建立;
2.坐标轴、坐标面;
3.根据坐标描出点的位置、由点的位置写出它的坐标的方法. 小结
直线、圆等几何图形就与方程f(x,y)=0建立对应关系,进而利用方程揭
示图形的有关性质.空间直角坐标系xyzO 从空间某一个定点O引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系O-xyz. 点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xOy平面、yOz平面和xOz平面. 在空间直角坐标系中,让右手拇指指向x轴的正方向,食指指向y轴的正方向,若中指指向z轴的正方向,则称这个坐标系为右手直角坐标系.
本书建立的坐标系都是右手直角坐标系.数学建构xyzO 通常,将空间直角坐标系画在纸上时, x轴与y轴、x轴与z轴均成135?,而z轴垂直于y轴. y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半,这样,三条轴上的单位长度在直观上大体相等. 对于空间任意一点A,作点A在三条坐标轴上
的射影,即通过点A作三个平面分别垂直
于x轴、y轴和z轴,它们与x轴、y轴和z轴分别交于P,Q,R.点P,Q,R
在相应数轴上的坐标依次为x,y,z,我们把有序实数组(x,y,z)叫做
点A的坐标,记为A(x,y,z). A空间直角坐标系画法与表示.数学建构在空间直角坐标系中,作出点P(5,4,6).xyzO数学应用D B CB?A?D?C?A x z y例2.如图,已知长方体ABCD-A?B?C?D?的边长为AB=12,AD=18,
AA?=5.以这个长方体的顶点A为坐标原点,射线AB,AD,AA?分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,求长方体各个顶点的坐标. 数学应用B1D B CB1A1D1C1A x z y已知正方体ABCD-A1B1C1D1的棱长为2, 写出正方体各顶点的坐标.建立适当空间直角坐标系.数学应用13zxyO 在正四棱锥S-ABCD中,建立如图所示的空间直角坐标系,根据条件,确定各顶点的坐标.SABCD数学应用点P(3,-2,1)关于坐标平面xOy的对称点的坐标为_________________;
点Q(-2,-3,1)关于原点的对称点的坐标为_________________;
点R(2,4,1)关于z轴的对称点的坐标为_____________________.P?(3,-2,-1)Q?(2,3,-1)R?(- 2,- 4,1)数学应用点P(x,y,z)关于
原点的对称点的坐标为______________________;
坐标平面xOy的对称点的坐标为_______________;
坐标平面yOz的对称点的坐标为_______________;
x轴的对称点的坐标为________________________;
z轴的对称点的坐标为________________________.P1(-x,-y,-z)空间任一点P(x,y,z)关于原点、轴、坐标平面的对称点的坐标特征.P2(x,y,-z)P5(-x,-y,z)P3(-x ,y,z)P4(x,-y,-z)数学建构1.下列点中,位于yoz平面内的是( )
A.(2,2,0) B.(0,2,2)
C.(2,0,2) D.(2,0,0)
2.点P(4,2,6)在xOy平面内射影P?的坐标是________.
3.点P(-2,-1,4)到xOz平面的距离是____________.B(4,2,0)1数学应用平面xOy内点的坐标特征为________________;
平面yOz内点的坐标特征为________________;
平面xOz内点的坐标特征为________________;
x轴上点的坐标特征为_____________________;
y轴上点的坐标特征为_____________________;
z轴上点的坐标特征为_____________________.空间内落在坐标轴上或坐标平面内的点的坐标特征. z=0 x=0 y=0 y=0,且z=0 x=0,且z=0 x=0,且y=0数学建构例3.(1)在空间直角坐标系O-xyz中,画出不共线的3个点P,Q,R,使得这3个点的坐标都满足z=3,并画出图形;
(2)写出由这三个点确定的平面内的点的坐标应满足的条件. xyzO数学应用 如图,已知四棱锥P-ABCD中,PA垂直于矩形ABCD所在平面,M是PC的中点,N在PB上,且PN=3NB,已知AB=4,AD=3,PA=5, 建立如图所示坐标系,写出点P,A,B,C,D,M,N的坐标.xyzAPBDCMN数学应用1.右手坐标系的建立;
2.坐标轴、坐标面;
3.根据坐标描出点的位置、由点的位置写出它的坐标的方法. 小结
