2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.2双曲线的几何性质课件(18张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.2.2双曲线的几何性质课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:38:22 | ||
图片预览






文档简介
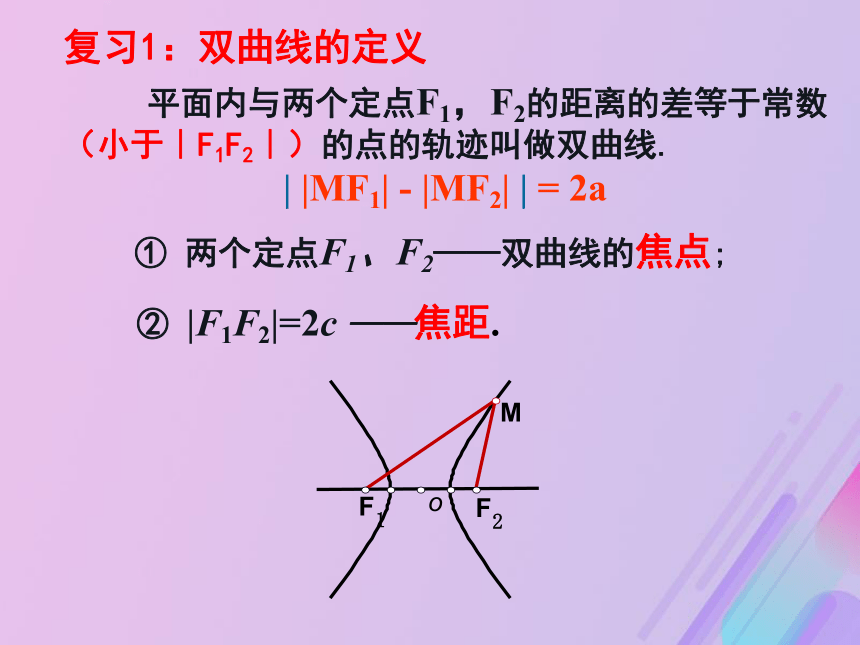
课件18张PPT。双曲线的简单几何性质复习1:双曲线的定义 平面内与两个定点F1,F2的距离的差等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
| |MF1| - |MF2| | = 2a
① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.类型一:
(焦点在x轴上,(-c,0)、 (c,0)) 类型二:
(焦点在y轴上,(0,-c)、(0,c))
其中复习1 双曲线的标准方程 类比椭圆几何性质的研究方法,我
们根据双曲线的标准方程
得出双曲线的范围、对称性、顶点等几何性质?问题1: 2、对称性 x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
(-x,y)(x,y)(x,-y)3、顶点(2)如图,线段A1A2叫做双曲线的实轴,它的长为2a,
a叫做实半轴长;线段B1B2叫做双曲线的虚轴,它的长
为2b,b叫做双曲线的虚半轴长.(3)实轴与虚轴等长的双曲线
叫等轴双曲线。(1)令y=0,得x=±a,则双曲线与x轴的两个交点为
A1(-a,0),A2(a,0),我们把这两个点叫双曲线的顶点;
令x=0,得y2=-b2,这个方程没有实数根,说明双曲线与y轴没有交点,但我们也把B1(0,-b),B2(0,b)画在y轴上。问题2:根据双曲线的标准方程
你能发现双曲线的范围还受到怎样的限制?由双曲线方程 ,可知即所以双曲线还应在上面两个不等式组表示的平面区域内,即以直线 和 为边界的平面区域内问题3:双曲线的范围在以直线 和 为边界的平面区域内,那么从x,y的变化趋势看,双曲线 和直线 具有怎样的关系?abPMN当x变大时, 变大,PM长趋向于0M(x,y)4、渐近线ab 可以看出,双曲线
的各支向外延伸时,与直线
逐渐接近,我们把这两条直线
叫做双曲线的渐近线。双曲线与渐近线无限接近,但永不相交。5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义:(2)e的范围:(3)e的含义:焦点在y轴上的双曲线的几何性质口答双曲线标准方程:双曲线性质:1.范围:2.对称性:3.顶点:4.渐近线方程:5.离心率:y≥a或y≤-a关于坐标轴和原点对称A1(0,-a),A2(0,a)A1A2为实轴,B1B2为虚轴解:把方程化为标准方程可得:实半轴长虚半轴长半焦距
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:例题讲解 巩固练习 1.中心在原点,实轴长为10,虚轴长为6的双曲线的标准
方程为( )A.C.BA.B.C.D.C2.双曲线 的渐近线方程为( )3.双曲线 的虚轴长是实轴长的2倍,
则m的值为例2:求下列双曲线的标准方程:例题讲解 法二:巧设方程,运用待定系数法.
⑴设双曲线方程为 ,法二:设双曲线方程为∴ 双曲线方程为∴ ,解之得k=4,1、“共渐近线”的双曲线的应用λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。双曲线的简单几何性质小 结对称轴:坐标轴
对称中心:原点A1,A2
| |MF1| - |MF2| | = 2a
① 两个定点F1、F2——双曲线的焦点;② |F1F2|=2c ——焦距.类型一:
(焦点在x轴上,(-c,0)、 (c,0)) 类型二:
(焦点在y轴上,(0,-c)、(0,c))
其中复习1 双曲线的标准方程 类比椭圆几何性质的研究方法,我
们根据双曲线的标准方程
得出双曲线的范围、对称性、顶点等几何性质?问题1: 2、对称性 x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
(-x,y)(x,y)(x,-y)3、顶点(2)如图,线段A1A2叫做双曲线的实轴,它的长为2a,
a叫做实半轴长;线段B1B2叫做双曲线的虚轴,它的长
为2b,b叫做双曲线的虚半轴长.(3)实轴与虚轴等长的双曲线
叫等轴双曲线。(1)令y=0,得x=±a,则双曲线与x轴的两个交点为
A1(-a,0),A2(a,0),我们把这两个点叫双曲线的顶点;
令x=0,得y2=-b2,这个方程没有实数根,说明双曲线与y轴没有交点,但我们也把B1(0,-b),B2(0,b)画在y轴上。问题2:根据双曲线的标准方程
你能发现双曲线的范围还受到怎样的限制?由双曲线方程 ,可知即所以双曲线还应在上面两个不等式组表示的平面区域内,即以直线 和 为边界的平面区域内问题3:双曲线的范围在以直线 和 为边界的平面区域内,那么从x,y的变化趋势看,双曲线 和直线 具有怎样的关系?abPMN当x变大时, 变大,PM长趋向于0M(x,y)4、渐近线ab 可以看出,双曲线
的各支向外延伸时,与直线
逐渐接近,我们把这两条直线
叫做双曲线的渐近线。双曲线与渐近线无限接近,但永不相交。5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义:(2)e的范围:(3)e的含义:焦点在y轴上的双曲线的几何性质口答双曲线标准方程:双曲线性质:1.范围:2.对称性:3.顶点:4.渐近线方程:5.离心率:y≥a或y≤-a关于坐标轴和原点对称A1(0,-a),A2(0,a)A1A2为实轴,B1B2为虚轴解:把方程化为标准方程可得:实半轴长虚半轴长半焦距
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:例题讲解 巩固练习 1.中心在原点,实轴长为10,虚轴长为6的双曲线的标准
方程为( )A.C.BA.B.C.D.C2.双曲线 的渐近线方程为( )3.双曲线 的虚轴长是实轴长的2倍,
则m的值为例2:求下列双曲线的标准方程:例题讲解 法二:巧设方程,运用待定系数法.
⑴设双曲线方程为 ,法二:设双曲线方程为∴ 双曲线方程为∴ ,解之得k=4,1、“共渐近线”的双曲线的应用λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。双曲线的简单几何性质小 结对称轴:坐标轴
对称中心:原点A1,A2
