2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.1.3导数的几何意义课件(30张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.1.3导数的几何意义课件(30张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:40:27 | ||
图片预览











文档简介
课件30张PPT。3.1.3 导数的几何意义
【教学目标】
知识与技能:理解导数的几何意义、熟练掌握求切点及函数“在一点处”型、“过一点”型的切线斜率的求法。
过程与方法:让学生体会割线斜率到切线斜率的过程,熟练掌握数形结合、分类讨论等数学思想方法。
情感态度与价值观:能够从生活中抽象出数学问题,在学习中养成积极探究,合作分享的学习态度。通过认真训练,达到举一反三、融会贯通的目的。
【重点、难点】
导数几何意义的理解与应用,“过一点”型的切线斜率的求解过程。 预习课本83页至84页,完成下列问题
一、基础概念:
1、割线斜率:
割线斜率就是函数的平均变化率
即:
2、切线斜率:
切线斜率就是割线斜率在某点取极限位置的斜率
即:
3、导数的几何意义:
曲线在某点处的切线斜率就等于该点的导数值
即:
问题探究:
思考1:割线斜率和切线斜率的关系?
参考:割线斜率是平均变化率,切线斜率是瞬时变化率,切线斜率是由割线斜率取极限得到的,是割线斜率的特殊状态。
思考2:本节切线的定义与以前学过的切线的定义有什么不同?
参考:本节中切线是利用割线的极限位置定义的,适用于任何曲线,以前学的切线是从直线与具体曲线的交点个数来定义的.比如直线和二次函数、圆、椭圆、双曲线、抛物线等二次曲线相切问题。
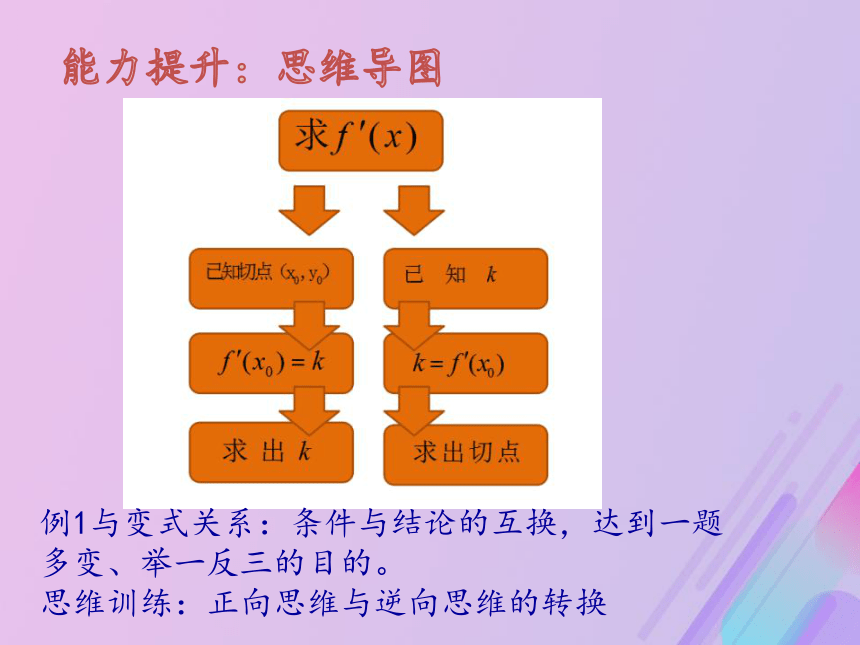
预习展评能力提升:思维导图例1与变式关系:条件与结论的互换,达到一题 多变、举一反三的目的。
思维训练:正向思维与逆向思维的转换
能力提升:思维导图常见的变式方向:
1、条件、结论的互换
2、条件、结论的要求改变
3、数据、位置等发生改变
4、知识点的改变
5、利用等价转换条件,转化不同的说法、形式能力形成:通过变式训练可以更好的理解知识点的本质,做到一题多变、多题一解,达到举一反三、融会贯通的目的。【课堂小结】
1、知识总结:
导数的几何意义、求切点、求斜率、求切线 方程
2、方法总结:
数形结合、分类讨论、转化
3、能力总结:
运算化简、变式能力、逻辑分析、合作探究课后作业:
A层作业:拓展案A、B,
预习导数的运算.
B层作业:拓展案C
老师寄语:
希望同学们发扬高铁精神,在学习中攻坚克难,学习效率越来越高,成绩越来越优秀!谢 谢
知识与技能:理解导数的几何意义、熟练掌握求切点及函数“在一点处”型、“过一点”型的切线斜率的求法。
过程与方法:让学生体会割线斜率到切线斜率的过程,熟练掌握数形结合、分类讨论等数学思想方法。
情感态度与价值观:能够从生活中抽象出数学问题,在学习中养成积极探究,合作分享的学习态度。通过认真训练,达到举一反三、融会贯通的目的。
【重点、难点】
导数几何意义的理解与应用,“过一点”型的切线斜率的求解过程。 预习课本83页至84页,完成下列问题
一、基础概念:
1、割线斜率:
割线斜率就是函数的平均变化率
即:
2、切线斜率:
切线斜率就是割线斜率在某点取极限位置的斜率
即:
3、导数的几何意义:
曲线在某点处的切线斜率就等于该点的导数值
即:
问题探究:
思考1:割线斜率和切线斜率的关系?
参考:割线斜率是平均变化率,切线斜率是瞬时变化率,切线斜率是由割线斜率取极限得到的,是割线斜率的特殊状态。
思考2:本节切线的定义与以前学过的切线的定义有什么不同?
参考:本节中切线是利用割线的极限位置定义的,适用于任何曲线,以前学的切线是从直线与具体曲线的交点个数来定义的.比如直线和二次函数、圆、椭圆、双曲线、抛物线等二次曲线相切问题。
预习展评能力提升:思维导图例1与变式关系:条件与结论的互换,达到一题 多变、举一反三的目的。
思维训练:正向思维与逆向思维的转换
能力提升:思维导图常见的变式方向:
1、条件、结论的互换
2、条件、结论的要求改变
3、数据、位置等发生改变
4、知识点的改变
5、利用等价转换条件,转化不同的说法、形式能力形成:通过变式训练可以更好的理解知识点的本质,做到一题多变、多题一解,达到举一反三、融会贯通的目的。【课堂小结】
1、知识总结:
导数的几何意义、求切点、求斜率、求切线 方程
2、方法总结:
数形结合、分类讨论、转化
3、能力总结:
运算化简、变式能力、逻辑分析、合作探究课后作业:
A层作业:拓展案A、B,
预习导数的运算.
B层作业:拓展案C
老师寄语:
希望同学们发扬高铁精神,在学习中攻坚克难,学习效率越来越高,成绩越来越优秀!谢 谢
