2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(18张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 220.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 08:41:21 | ||
图片预览




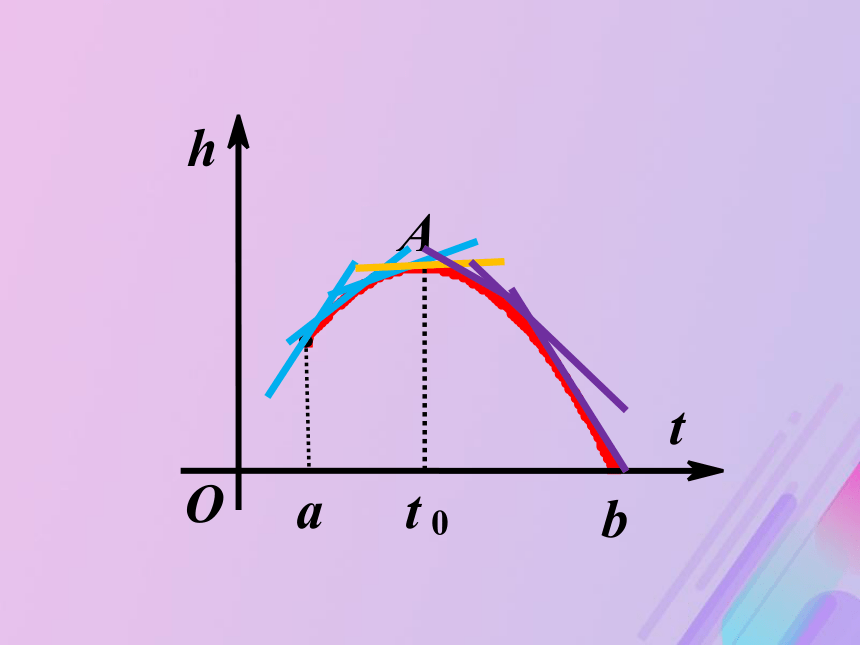


文档简介
课件18张PPT。§3.3.1利用导数判断函数的单调性 1. 函数的单调性:
对于任意的两个数x1,x2∈I,且当x1<x2时,都有f(x1)<f(x2),那么函数f(x)就是区间I上的增函数.
对于任意的两个数x1,x2∈I,且当x1<x2时,都有f(x1)>f(x2),那么函数f(x)就是区间I上的减函数.2. 导数的概念及其四则运算复习引入3.y=f(x)在x=x0处导数的几何意义竖直上抛一个小沙袋,沙袋的高度h是时间t的函数,设h=h(t),其图象如图所示。 横轴表示时间t,纵轴表示沙袋的高度h,设沙袋的最高点为A,其横坐标为t=t0. 先考察沙袋在区间(a,t0)的运动情况: 根据生活经验,我们知道,在这个区间内,沙袋向上运动,其竖直向上的瞬时速度大于0, 引入新课即在区间(a,t0), 我们说在此区间内,函数h=h(t)是增函数.再考察沙袋在区间(t0,b)的运动情况:在这个区间内,沙袋向下运动,其竖直向上的瞬时速度小于0,即在区间(t0,b), 我们说在此区间内,函数h=h(t)是减函数。用函数的导数判断函数单调性的法则:1.如果在区间(a,b)内,f ′ (x)>0,则f(x)在此区间是增函数,(a,b)为f(x)的单调增区间;
2.如果在区间(a,b)内,f ′ (x)<0,则f(x)在此区间是减函数,(a,b)为f(x)的单调减区间;例1.如图,设有圆C和定点O,当l 从l0 开始在平面上绕O点匀速旋转(旋转角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,它的图象大致是下列四种情况中的哪一种?应用举例解:由于是匀速旋转,阴影部分的面积S(t)开始和最后时段缓慢增加,中间时段S增速快,
图A表示S的增速是常数,与实际不符,图A应否定;
图B表示最后时段S的增速快,也与实际不符,图B也应否定;
图C表示开始时段与最后时段S的增速快,也与实际不符,图C也应否定;
图D表示开始与结束时段,S的增速慢,中间的时段增速快,符合实际,应选D。例2.确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f ′ (x)=(x2-2x+4) ′=2x-2.令2x-2>0,解得x>1.∴当x∈(1,+∞)时,f ′ (x)>0,
f(x)是增函数.令2x-2<0,解得x<1.∴当x∈(-∞,1)时,f ′ (x)<0,
f(x)是减函数.例3.找出函数f(x)=x3-4x2+x-1的单调区间。解:f ′ (x)=3x2-8x+1,
令3x2-8x+1>0,解此不等式得 或令3x2-8x+1<0,解此不等式得 因此,区间 为f(x)的单调减区间。1.函数y=3x-x3的单调增区间是( )
(A) (0,+∞) (B) (-∞,-1)
(C) (-1,1) (D) (1,+∞)C课堂练习2.设f(x)=x+ (x<0),则f(x)的单调增区间是( )
(A) (-∞,-2) (B) (-2,0)
(C) (-∞,- ) (D) (- ,0)C3.函数y=xlnx在区间(0,1)上是( )
(A)单调增函数
(B)单调减函数
(C) 在(0, )上是减函数,在( , 1)上是增函数
(D) 在( , 1)上是减函数,在(0, )上是增函数C4.函数y=x2(x+3)的减区间是 ,增区间是 .(-2,0) (-∞,-2)及(0,+∞) 5.函数f(x)=cos2x的单调区间是
.(kπ, kπ+ ), k∈Z 6.当x>1时,证明不等式: 证明:设f(x)= 显然,f(x)在[1,∞)上连续,且f(1)=0. f ′ (x)=∵ x>1, ∴ >0,于是f ′ (x)>0. 故f(x)是[1,+∞)上的增函数,应有:
当x>1时,f(x)>f(1)=0, 即当x>1时,课堂小结:用函数的导数判断函数单调性的法则再见
对于任意的两个数x1,x2∈I,且当x1<x2时,都有f(x1)<f(x2),那么函数f(x)就是区间I上的增函数.
对于任意的两个数x1,x2∈I,且当x1<x2时,都有f(x1)>f(x2),那么函数f(x)就是区间I上的减函数.2. 导数的概念及其四则运算复习引入3.y=f(x)在x=x0处导数的几何意义竖直上抛一个小沙袋,沙袋的高度h是时间t的函数,设h=h(t),其图象如图所示。 横轴表示时间t,纵轴表示沙袋的高度h,设沙袋的最高点为A,其横坐标为t=t0. 先考察沙袋在区间(a,t0)的运动情况: 根据生活经验,我们知道,在这个区间内,沙袋向上运动,其竖直向上的瞬时速度大于0, 引入新课即在区间(a,t0), 我们说在此区间内,函数h=h(t)是增函数.再考察沙袋在区间(t0,b)的运动情况:在这个区间内,沙袋向下运动,其竖直向上的瞬时速度小于0,即在区间(t0,b), 我们说在此区间内,函数h=h(t)是减函数。用函数的导数判断函数单调性的法则:1.如果在区间(a,b)内,f ′ (x)>0,则f(x)在此区间是增函数,(a,b)为f(x)的单调增区间;
2.如果在区间(a,b)内,f ′ (x)<0,则f(x)在此区间是减函数,(a,b)为f(x)的单调减区间;例1.如图,设有圆C和定点O,当l 从l0 开始在平面上绕O点匀速旋转(旋转角度不超过90°)时,它扫过的圆内阴影部分的面积S是时间t的函数,它的图象大致是下列四种情况中的哪一种?应用举例解:由于是匀速旋转,阴影部分的面积S(t)开始和最后时段缓慢增加,中间时段S增速快,
图A表示S的增速是常数,与实际不符,图A应否定;
图B表示最后时段S的增速快,也与实际不符,图B也应否定;
图C表示开始时段与最后时段S的增速快,也与实际不符,图C也应否定;
图D表示开始与结束时段,S的增速慢,中间的时段增速快,符合实际,应选D。例2.确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f ′ (x)=(x2-2x+4) ′=2x-2.令2x-2>0,解得x>1.∴当x∈(1,+∞)时,f ′ (x)>0,
f(x)是增函数.令2x-2<0,解得x<1.∴当x∈(-∞,1)时,f ′ (x)<0,
f(x)是减函数.例3.找出函数f(x)=x3-4x2+x-1的单调区间。解:f ′ (x)=3x2-8x+1,
令3x2-8x+1>0,解此不等式得 或令3x2-8x+1<0,解此不等式得 因此,区间 为f(x)的单调减区间。1.函数y=3x-x3的单调增区间是( )
(A) (0,+∞) (B) (-∞,-1)
(C) (-1,1) (D) (1,+∞)C课堂练习2.设f(x)=x+ (x<0),则f(x)的单调增区间是( )
(A) (-∞,-2) (B) (-2,0)
(C) (-∞,- ) (D) (- ,0)C3.函数y=xlnx在区间(0,1)上是( )
(A)单调增函数
(B)单调减函数
(C) 在(0, )上是减函数,在( , 1)上是增函数
(D) 在( , 1)上是减函数,在(0, )上是增函数C4.函数y=x2(x+3)的减区间是 ,增区间是 .(-2,0) (-∞,-2)及(0,+∞) 5.函数f(x)=cos2x的单调区间是
.(kπ, kπ+ ), k∈Z 6.当x>1时,证明不等式: 证明:设f(x)= 显然,f(x)在[1,∞)上连续,且f(1)=0. f ′ (x)=∵ x>1, ∴ >0,于是f ′ (x)>0. 故f(x)是[1,+∞)上的增函数,应有:
当x>1时,f(x)>f(1)=0, 即当x>1时,课堂小结:用函数的导数判断函数单调性的法则再见
