2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性(18张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 725.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:02:13 | ||
图片预览


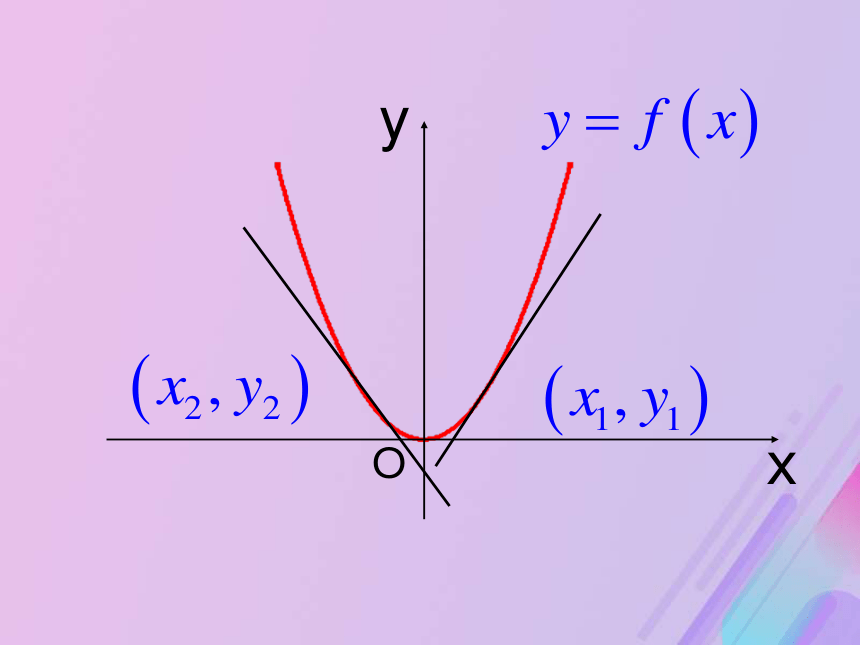

文档简介
课件18张PPT。利用导数判断函数的单调性
从a到b曲线是上升的,说函数f(x)在区间(a,b)上是增函数; 从b到c曲线是下降的,说函数f(x)在区间(b,c)上是减函数. 讨论函数 的单调性
学习目标
重点与难点
重点:会用导数求函数的单调区间
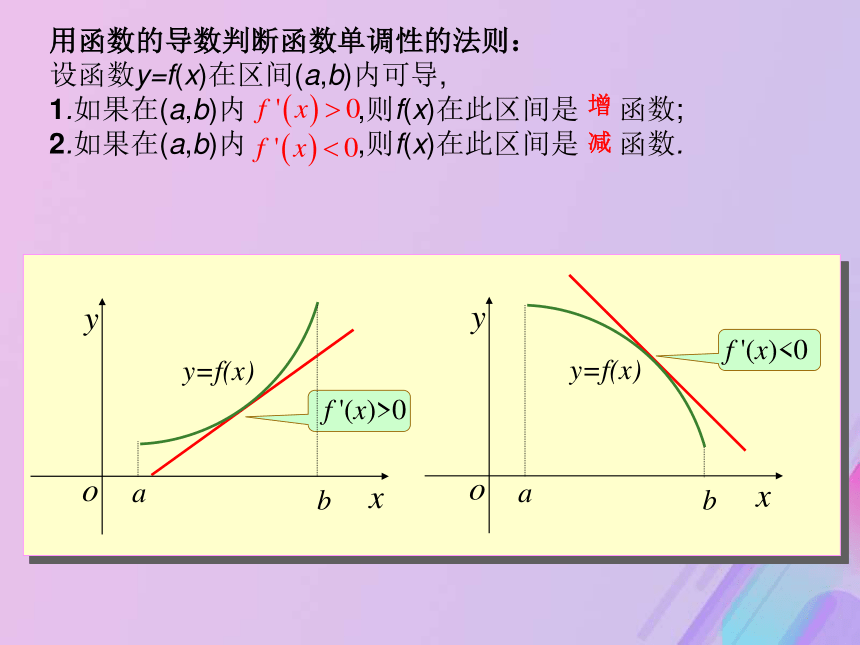
难点:函数的单调性与导数的关系f '(x)>0f '(x)<0 用函数的导数判断函数单调性的法则:
设函数y=f(x)在区间(a,b)内可导,
1.如果在(a,b)内 ,则f(x)在此区间是 函数;
2.如果在(a,b)内 ,则f(x)在此区间是 函数.
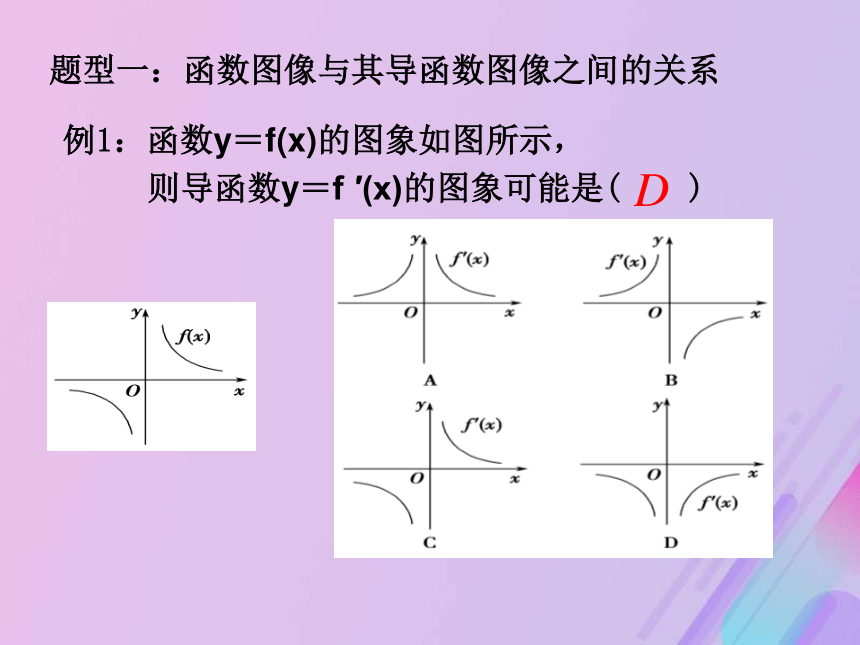
增减题型一:函数图像与其导函数图像之间的关系例1:函数y=f(x)的图象如图所示,
则导函数y=f ′(x)的图象可能是( )
练习1:设函数f(x)在定义域内可导,y=f(x)
的图象如图所示,则导函数 y=f ′(x)的图像可能为( ) 总结:导函数f′(x)的图象看正负,
原函数f(x)的图象看增减。 例2:导函数y=f ′(x)的图象如图所示, 则y=f(x)的图象最有可能的是( ) 练习2:已知函数y=xf ′(x)的图象如图所示,下面四个图象中能大致表示y=f(x)的图象的是( ) 题型二:利用导数求函数单调区间 例1:求函数 的单调区间练习:求函数 的单调区间
利用导数讨论函数单调区间的步骤(2)求导数 ;(1)确定函数 的定义域;(3)解不等式 ,解集在定义域内的部分为增区间; 解不等式 ,解集在定义域内的部分为减区间.例2:求函数 的单调区间练习:求函数 的单调区间例3:求函数 的单调区间练习:求函数 的单调区间例4:求函数 的单调区间练习:求函数 的单调区间小结1、这节课你的收获是:
2、解题过程中有哪些问题需注意:已知函数 试讨论此函数的单调区间
解:
令 >0,
解得 或
∴单调增区间是(-∞,-1)和(1,+∞).
令 <0,解得 或
∴单调减区间是(-1,0)和(0,1)
学习目标
重点与难点
重点:会用导数求函数的单调区间
难点:函数的单调性与导数的关系f '(x)>0f '(x)<0 用函数的导数判断函数单调性的法则:
设函数y=f(x)在区间(a,b)内可导,
1.如果在(a,b)内 ,则f(x)在此区间是 函数;
2.如果在(a,b)内 ,则f(x)在此区间是 函数.
增减题型一:函数图像与其导函数图像之间的关系例1:函数y=f(x)的图象如图所示,
则导函数y=f ′(x)的图象可能是( )
练习1:设函数f(x)在定义域内可导,y=f(x)
的图象如图所示,则导函数 y=f ′(x)的图像可能为( ) 总结:导函数f′(x)的图象看正负,
原函数f(x)的图象看增减。 例2:导函数y=f ′(x)的图象如图所示, 则y=f(x)的图象最有可能的是( ) 练习2:已知函数y=xf ′(x)的图象如图所示,下面四个图象中能大致表示y=f(x)的图象的是( ) 题型二:利用导数求函数单调区间 例1:求函数 的单调区间练习:求函数 的单调区间
利用导数讨论函数单调区间的步骤(2)求导数 ;(1)确定函数 的定义域;(3)解不等式 ,解集在定义域内的部分为增区间; 解不等式 ,解集在定义域内的部分为减区间.例2:求函数 的单调区间练习:求函数 的单调区间例3:求函数 的单调区间练习:求函数 的单调区间例4:求函数 的单调区间练习:求函数 的单调区间小结1、这节课你的收获是:
2、解题过程中有哪些问题需注意:已知函数 试讨论此函数的单调区间
解:
令 >0,
解得 或
∴单调增区间是(-∞,-1)和(1,+∞).
令 <0,解得 或
∴单调减区间是(-1,0)和(0,1)
