2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.2.2“非”(否定)课件(34张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.2.2“非”(否定)课件(34张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:13:28 | ||
图片预览









文档简介
课件34张PPT。1.2.2 “非”(否定)温故知新
1.“且”、“或”的含义是什么?
2.如何判断由“且”、“或”构成的新命题的真假?
【学习目标】
1.了解逻辑联结词“非”的意义,会写一个命题的否定命题,能判断否定命题的真假.
2.会对含有全称量词、存在量词的全称命题,存在性命题进行否定.
3.体会命题间的逻辑关系
学习重点:写出所给命题的否定命题,并判断真假.
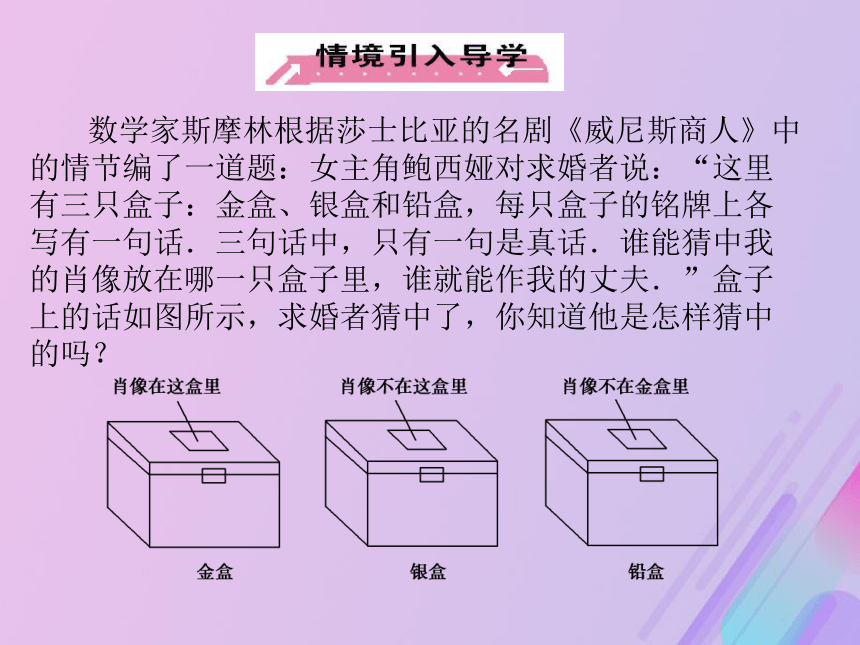
学习难点:全称命题,存在性命题的否定和真假判断.数学家斯摩林根据莎士比亚的名剧《威尼斯商人》中的情节编了一道题:女主角鲍西娅对求婚者说:“这里有三只盒子:金盒、银盒和铅盒,每只盒子的铭牌上各写有一句话.三句话中,只有一句是真话.谁能猜中我的肖像放在哪一只盒子里,谁就能作我的丈夫.”盒子上的话如图所示,求婚者猜中了,你知道他是怎样猜中的吗?提示:金盒上的铭牌“肖像在这盒里”(即肖像在金盒里)与铅盒上面的铭牌“肖像不在金盒里”是两个命题,其中一个是另一个的否定,由逻辑知识可知,它们一真一假.又因为三句话中只有一句是真话,所以银盒的铭牌所说的那句话“肖像不在这盒里”就肯定是假话了,于是求婚者断定鲍西娅的肖像放在银盒子里.1.“非”的含义
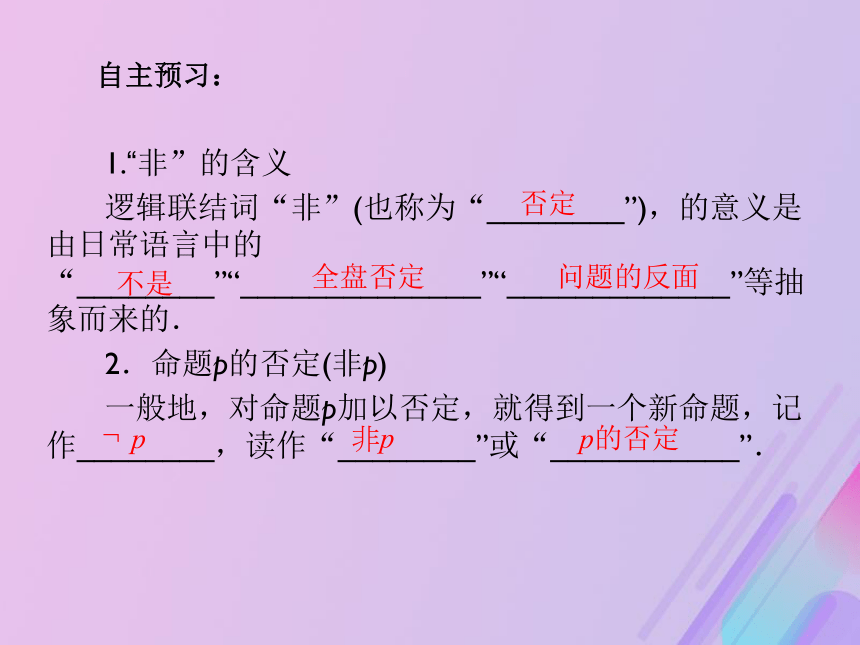
逻辑联结词“非”(也称为“________”),的意义是由日常语言中的“________”“______________”“_____________”等抽象而来的.
2.命题p的否定(非p)
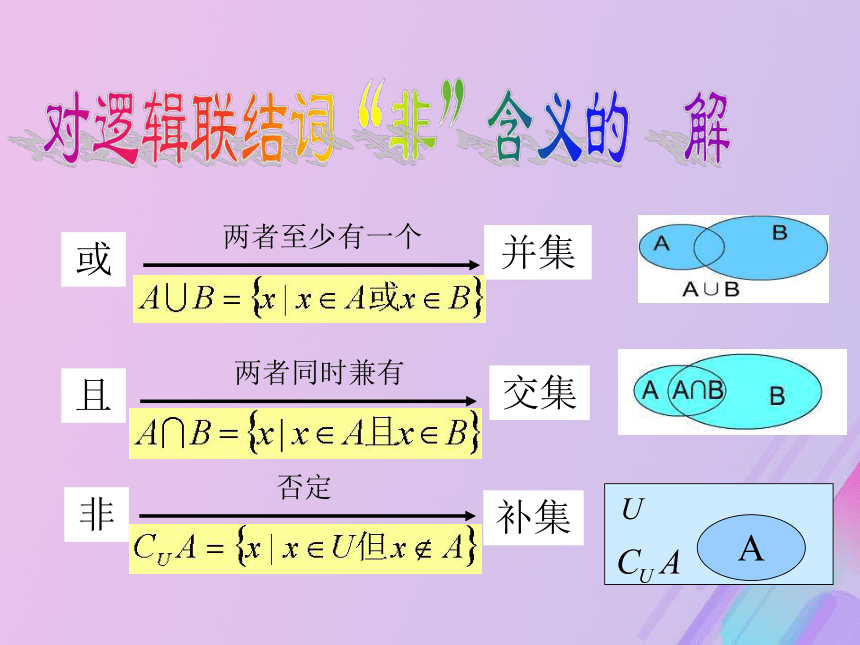
一般地,对命题p加以否定,就得到一个新命题,记作________,读作“________”或“___________”.否定 不是全盘否定问题的反面 p的否定 綈p非p自主预习:或且非并集交集补集对逻辑联结词“非”含义的理解一般把如何由p的真假判定綈p的真假总结为下表:
注:p的否定是綈p,綈p的否定是p,即p与綈p是相互否定的.假假3.存在性命题的否定
存在性命题p:?x∈A,p(x);它的否定是綈p:___________________.
4.全称命题的否定
全称命题q:?x∈A,q(x);它的否定是綈q:____________________.?x∈A,綈p(x)?x∈A,綈q(x)注:否定存在性命题时,首先把存在量词改为全称量词,再对性质p(x)进行否定.
注:否定全称命题时,首先把全称量词改为存在量词,再对性质q(x)进行否定.
(2)7班的同学都是庄河人;(3)7班的同学都不是庄河人;(4)7班的同学不都是庄河人.写出下列命题的否定,并判断真假:(1)7班的同学至少有一人是庄河人;常用正面词语的否定
写出命题的非(否定),需要对其正面叙述的词语进行否定,常用正面叙述词语及它的否定列举如下:不大于
(≤)不等于
不小于
(≥)不是不都是至少有两个
一个也没有
例1:写出下列命题的否定,并判断其真假:
(1)p: y=tanx是奇函数;
(2)q:
(3)r: 抛物线y=(x-1)2的顶点是(1,0)【合作探究】写出下列命题的否定。
(1)
?
(2)
?
(3)若x2-x≠0,则x≠0且x≠1.
小结:命题“p且q”的否定是“綈p”或“綈q”;
命题“p或q”的否定是“綈p且綈q”.
跟踪训练:
1.若命题p:x∈A∪B,则 p是( )
A.x∈A∪B B.x?A或x?B
C.x?A且x?B D.x∈A∩B
(1)p:
(2)q: 所有的正方形都是矩形;
(3)r:
(4)s: 至少有一个实数x,使x3+1=0例2:写出下列命题的否定,并判断其真假:
[方法总结] 1.对全称命题否定的两个步骤
第一步改变量词:把全称量词换为恰当的存在量词;
第二步否定性质:原命题中的“p(x)成立”改为“綈p(x)成立”.
2.全称命题否定后的真假判断方法
全称命题的否定是存在性命题,其真假性与全称命题相反;要说明一个全称命题是假命题,只需举一个反例即可.
[方法总结] 1.对存在性命题否定的步骤
第一步改变量词:把存在量词换为恰当的全称量词.
第二步否定性质:原命题中的“p(x)成立”否定为“綈p(x)成立”.
2.存在性命题否定后的真假判断
存在性命题的否定是全称命题,其真假性与存在性命题相反;要说明一个存在性命题是真命题,只需要找到一个实例即可.2.(2013·四川高考)设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:?x∈A,2x∈B,则( )
A.綈p:?x∈A,2x∈B B.綈p:?x?A,2x∈B
C.綈p:?x∈A,2x?B D.綈p:?x?A,2x?B
[答案] C
由命题p:?x∈A,2x∈B得綈p:?x∈A,2x?B.跟踪训练: 1.命题“ x∈R,x3-x2+1≤0”的否定_________
[方法总结] 1.对全称命题否定的两个步骤
第一步改变量词:把全称量词换为恰当的存在量词;
第二步否定性质:原命题中的“p(x)成立”改为“綈p(x)成立”.3.已知命题p: ? x∈R,sinx≤1,则( )
A. ∶ ? x∈R,sinx≥1
B、 ∶?x∈R,sinx≤1
C. ∶?x∈R,sinx>1
D. ∶?x∈R,sinx>1 跟踪训练:4.(2013·九江高二检测)命题:存在n∈N,2n>1000的否定是( )
A.任意n∈N,2n≤1000
B.任意n∈N,2n>1000
C.存在n∈N,2n≤1000
D.存在n∈N,2n<1000跟踪训练:
[方法总结] 1.对存在性命题否定的步骤
第一步改变量词:把存在量词换为恰当的全称量词.
第二步否定性质:原命题中的“p(x)成立”否定为“綈p(x)成立”.命题方向:全称命题、存在性命题的真假判断 5.(2014.大连二模)下列命题中的假命题是( )
A.B.C.D.6.写出下列命题p的否定,并判断其真假:
①p:有些三角形是直角三角形
②p:所有的质数都是奇数跟踪训练:
[方法总结] 1.全称命题否定后的真假判断方法
全称命题的否定是存在性命题,其真假性与全称命题相反;要说明一个全称命题是假命题,只需举一个反例即可.
2.存在性命题否定后的真假判断
存在性命题的否定是全称命题,其真假性与存在性命题相反;要说明一个存在性命题是真命题,只需要找到一个实例即可.
拓展探究:函数与方程思想及其转化思想
若“ ”为假命题,则
实数 的取值范围_________________.
[方法总结] 1.注意命题真假之间的等价转化形式
命题与命题的否定之间的等价转化,表现在:若已知命题p为假,常常转化为綈p为真进行解题.另外本例也可以间接求得参数m的取值范围:若原命题为真命题,只需m>f(x)min=1,所以原命题为假命题的参数m的取值范围是m≤1.课堂小结:1、 “ ”形式的命题及其真假
2、全称命题的否定与存在性命题的否定及其真假知识方面:思想方法方面:函数与方程的思想及转化思想(必做题)
1、自己写一个数学命题,写出它否定,并判断它们的真假;
2、完成教材 练习A,练习B
(选做题)
已知命题 ,
若命题“ ”是真命题,求实数a的取值范围。
?
?
?
?
1.“且”、“或”的含义是什么?
2.如何判断由“且”、“或”构成的新命题的真假?
【学习目标】
1.了解逻辑联结词“非”的意义,会写一个命题的否定命题,能判断否定命题的真假.
2.会对含有全称量词、存在量词的全称命题,存在性命题进行否定.
3.体会命题间的逻辑关系
学习重点:写出所给命题的否定命题,并判断真假.
学习难点:全称命题,存在性命题的否定和真假判断.数学家斯摩林根据莎士比亚的名剧《威尼斯商人》中的情节编了一道题:女主角鲍西娅对求婚者说:“这里有三只盒子:金盒、银盒和铅盒,每只盒子的铭牌上各写有一句话.三句话中,只有一句是真话.谁能猜中我的肖像放在哪一只盒子里,谁就能作我的丈夫.”盒子上的话如图所示,求婚者猜中了,你知道他是怎样猜中的吗?提示:金盒上的铭牌“肖像在这盒里”(即肖像在金盒里)与铅盒上面的铭牌“肖像不在金盒里”是两个命题,其中一个是另一个的否定,由逻辑知识可知,它们一真一假.又因为三句话中只有一句是真话,所以银盒的铭牌所说的那句话“肖像不在这盒里”就肯定是假话了,于是求婚者断定鲍西娅的肖像放在银盒子里.1.“非”的含义
逻辑联结词“非”(也称为“________”),的意义是由日常语言中的“________”“______________”“_____________”等抽象而来的.
2.命题p的否定(非p)
一般地,对命题p加以否定,就得到一个新命题,记作________,读作“________”或“___________”.否定 不是全盘否定问题的反面 p的否定 綈p非p自主预习:或且非并集交集补集对逻辑联结词“非”含义的理解一般把如何由p的真假判定綈p的真假总结为下表:
注:p的否定是綈p,綈p的否定是p,即p与綈p是相互否定的.假假3.存在性命题的否定
存在性命题p:?x∈A,p(x);它的否定是綈p:___________________.
4.全称命题的否定
全称命题q:?x∈A,q(x);它的否定是綈q:____________________.?x∈A,綈p(x)?x∈A,綈q(x)注:否定存在性命题时,首先把存在量词改为全称量词,再对性质p(x)进行否定.
注:否定全称命题时,首先把全称量词改为存在量词,再对性质q(x)进行否定.
(2)7班的同学都是庄河人;(3)7班的同学都不是庄河人;(4)7班的同学不都是庄河人.写出下列命题的否定,并判断真假:(1)7班的同学至少有一人是庄河人;常用正面词语的否定
写出命题的非(否定),需要对其正面叙述的词语进行否定,常用正面叙述词语及它的否定列举如下:不大于
(≤)不等于
不小于
(≥)不是不都是至少有两个
一个也没有
例1:写出下列命题的否定,并判断其真假:
(1)p: y=tanx是奇函数;
(2)q:
(3)r: 抛物线y=(x-1)2的顶点是(1,0)【合作探究】写出下列命题的否定。
(1)
?
(2)
?
(3)若x2-x≠0,则x≠0且x≠1.
小结:命题“p且q”的否定是“綈p”或“綈q”;
命题“p或q”的否定是“綈p且綈q”.
跟踪训练:
1.若命题p:x∈A∪B,则 p是( )
A.x∈A∪B B.x?A或x?B
C.x?A且x?B D.x∈A∩B
(1)p:
(2)q: 所有的正方形都是矩形;
(3)r:
(4)s: 至少有一个实数x,使x3+1=0例2:写出下列命题的否定,并判断其真假:
[方法总结] 1.对全称命题否定的两个步骤
第一步改变量词:把全称量词换为恰当的存在量词;
第二步否定性质:原命题中的“p(x)成立”改为“綈p(x)成立”.
2.全称命题否定后的真假判断方法
全称命题的否定是存在性命题,其真假性与全称命题相反;要说明一个全称命题是假命题,只需举一个反例即可.
[方法总结] 1.对存在性命题否定的步骤
第一步改变量词:把存在量词换为恰当的全称量词.
第二步否定性质:原命题中的“p(x)成立”否定为“綈p(x)成立”.
2.存在性命题否定后的真假判断
存在性命题的否定是全称命题,其真假性与存在性命题相反;要说明一个存在性命题是真命题,只需要找到一个实例即可.2.(2013·四川高考)设x∈Z,集合A是奇数集,集合B是偶数集.若命题p:?x∈A,2x∈B,则( )
A.綈p:?x∈A,2x∈B B.綈p:?x?A,2x∈B
C.綈p:?x∈A,2x?B D.綈p:?x?A,2x?B
[答案] C
由命题p:?x∈A,2x∈B得綈p:?x∈A,2x?B.跟踪训练: 1.命题“ x∈R,x3-x2+1≤0”的否定_________
[方法总结] 1.对全称命题否定的两个步骤
第一步改变量词:把全称量词换为恰当的存在量词;
第二步否定性质:原命题中的“p(x)成立”改为“綈p(x)成立”.3.已知命题p: ? x∈R,sinx≤1,则( )
A. ∶ ? x∈R,sinx≥1
B、 ∶?x∈R,sinx≤1
C. ∶?x∈R,sinx>1
D. ∶?x∈R,sinx>1 跟踪训练:4.(2013·九江高二检测)命题:存在n∈N,2n>1000的否定是( )
A.任意n∈N,2n≤1000
B.任意n∈N,2n>1000
C.存在n∈N,2n≤1000
D.存在n∈N,2n<1000跟踪训练:
[方法总结] 1.对存在性命题否定的步骤
第一步改变量词:把存在量词换为恰当的全称量词.
第二步否定性质:原命题中的“p(x)成立”否定为“綈p(x)成立”.命题方向:全称命题、存在性命题的真假判断 5.(2014.大连二模)下列命题中的假命题是( )
A.B.C.D.6.写出下列命题p的否定,并判断其真假:
①p:有些三角形是直角三角形
②p:所有的质数都是奇数跟踪训练:
[方法总结] 1.全称命题否定后的真假判断方法
全称命题的否定是存在性命题,其真假性与全称命题相反;要说明一个全称命题是假命题,只需举一个反例即可.
2.存在性命题否定后的真假判断
存在性命题的否定是全称命题,其真假性与存在性命题相反;要说明一个存在性命题是真命题,只需要找到一个实例即可.
拓展探究:函数与方程思想及其转化思想
若“ ”为假命题,则
实数 的取值范围_________________.
[方法总结] 1.注意命题真假之间的等价转化形式
命题与命题的否定之间的等价转化,表现在:若已知命题p为假,常常转化为綈p为真进行解题.另外本例也可以间接求得参数m的取值范围:若原命题为真命题,只需m>f(x)min=1,所以原命题为假命题的参数m的取值范围是m≤1.课堂小结:1、 “ ”形式的命题及其真假
2、全称命题的否定与存在性命题的否定及其真假知识方面:思想方法方面:函数与方程的思想及转化思想(必做题)
1、自己写一个数学命题,写出它否定,并判断它们的真假;
2、完成教材 练习A,练习B
(选做题)
已知命题 ,
若命题“ ”是真命题,求实数a的取值范围。
?
?
?
?
