2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.3.1推出与充分条件、必要条件课件(23张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.3.1推出与充分条件、必要条件课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 00:00:00 | ||
图片预览







文档简介
课件23张PPT。 第2课时
充分条件与必要条件1.理解充分条件和必要条件的含义.
2.会判断两个条件间的充分必要关系.
3.能利用条件间的充分必要关系求参数的取值范围.函数y=xcos x+sin x的图像大致为( ).必要p?q充分充分 p与q的推出情况和p与q的充分、必要性有何联系?
(1)若 ,则p是q的充分不必要条件;?
(2)若 ,则p是q的必要不充分条件;?
(3)若 ,则p是q的充要条件;?
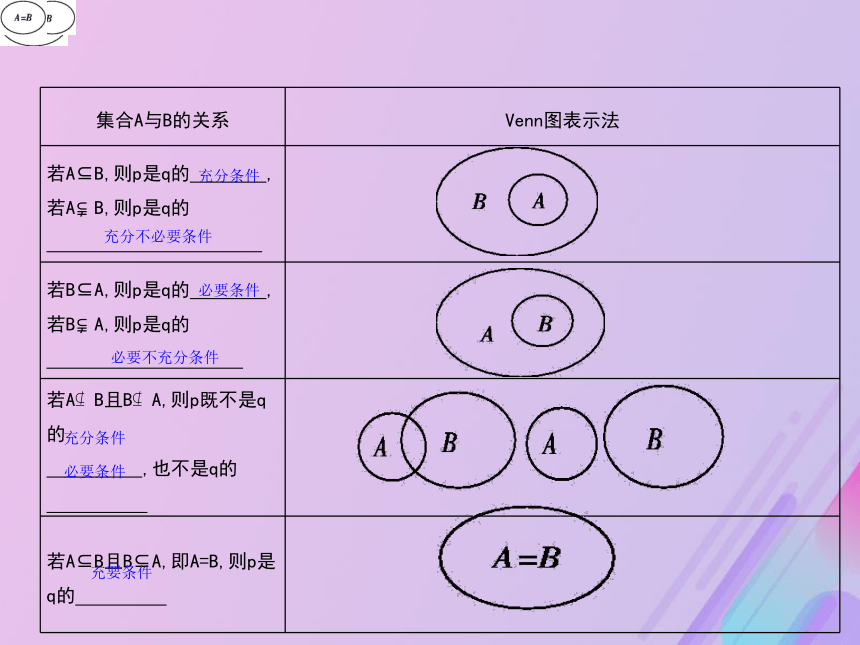
(4)若 ,则p是q的既不充分也不必要条件.?p?q,且q?pp?/ q,且q?pp?/ q,且q?/ pp?q,且q?/ p 如何从集合的角度理解充分条件、必要条件和充要条件?
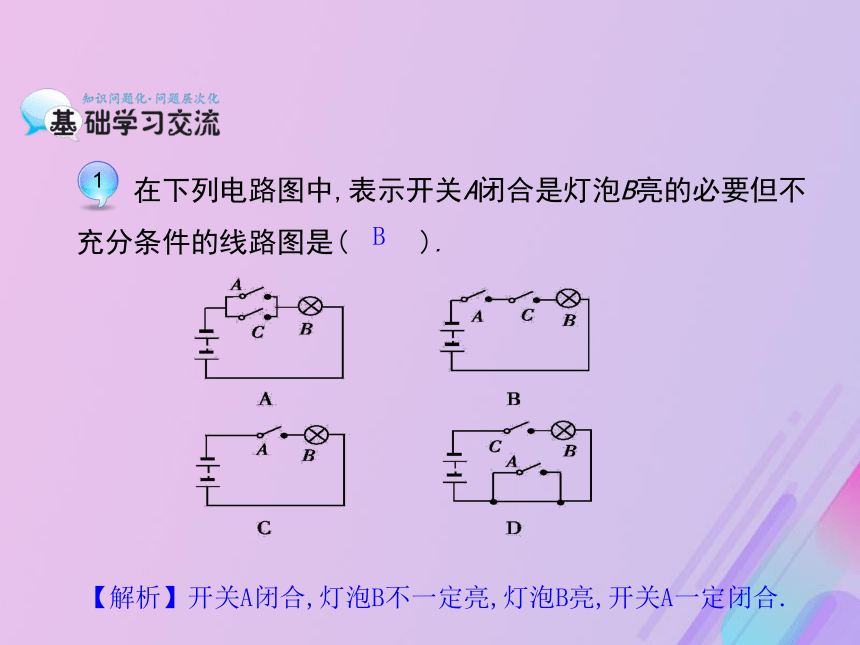
建立与p、q相应的集合,即p:A={x|p(x)},q:B={x|q(x)}.充分条件充分不必要条件必要条件必要不充分条件充分条件必要条件充要条件 在下列电路图中,表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是( ).B【解析】开关A闭合,灯泡B不一定亮,灯泡B亮,开关A一定闭合.A 已知q是等比数列{an}的公比,则“q<1”是“数列{an}是递减数列”的 条件.?
【解析】由数列{an}是递减数列可得0 指出下列各题中,p是q的什么条件?
(1)p:∠A=∠B,q:∠A和∠B是对顶角.
(2)p:x=1,q:x2=1.
【解析】(1)∵p?/ q且q?p,∴p是q的必要不充分条件.
(2)∵q:x2=1?x=1或x=-1,∴x=1?x2=1,但x2=1?/ x=1,
∴p是q的充分不必要条件.必要不充分充分条件、必要条件、充要条件的判断
分析下面的各组命题中p是q的什么条件.(从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一个)
(1)在△ABC中,p:∠A=∠B,q:sin A=sin B.
(2)非空集合A、B中,p:x∈A∪B,q:x∈B.【解析】(1)在△ABC中,∠A=∠B?sin A=sin B,反之,若sin A=sin B,因为A与B不可能互补(因为三角形三个内角和为180°),所以只有A=B.故p是q的充要条件.
(2)显然x∈A∪B不一定有x∈B,但x∈B一定有x∈A∪B,所以p是q的必要不充分条件.7根据充分条件、必要条件求参数的取值范围
已知p:A={x∈R|x2+ax+1≤0},q:B={x∈R|x2-3x+2≤0},若p是q的充分不必要条件,求实数a的取值范围.充要条件的探求与证明
已知方程x2+(2k-1)x+k2=0,求使方程有两个大于1的根的充要条件.[问题]使方程有两个大于1的根的充要条件是k<-1吗? 已知命题p:1-c0),命题q:x>7或x<-1,并且p是q的既不充分又不必要条件,则c的取值范围是 .?求关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件.C1.设集合A,B,则“A?B”是“A∩B=A成立”的( ).
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】由A?B,得A∩B=A;反过来,由A∩B=A,且(A∩B)?B,得A?B.因此,“A?B”是“A∩B=A成立”的充要条件.2.已知平面α,β,直线m?平面α,则“平面α∥平面β”是“直线m∥平面β”的( ).
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
【解析】因为平面α∥平面β且直线m?平面α,所以直线m∥平面β,反之,当直线m∥平面β时,直线m?平面α,也可能平面α和平面β相交. A
3.设有如下三个命题:
甲: m∩l=A,m,l?α,m,l?β;
乙:直线m,l中至少有一条与平面β相交;
丙:平面α与平面β相交.
当甲成立时,乙是丙的 条件.?
【解析】由题意乙?丙,丙?乙.
故当甲成立时,乙是丙的充要条件.充要
充分条件与必要条件1.理解充分条件和必要条件的含义.
2.会判断两个条件间的充分必要关系.
3.能利用条件间的充分必要关系求参数的取值范围.函数y=xcos x+sin x的图像大致为( ).必要p?q充分充分 p与q的推出情况和p与q的充分、必要性有何联系?
(1)若 ,则p是q的充分不必要条件;?
(2)若 ,则p是q的必要不充分条件;?
(3)若 ,则p是q的充要条件;?
(4)若 ,则p是q的既不充分也不必要条件.?p?q,且q?pp?/ q,且q?pp?/ q,且q?/ pp?q,且q?/ p 如何从集合的角度理解充分条件、必要条件和充要条件?
建立与p、q相应的集合,即p:A={x|p(x)},q:B={x|q(x)}.充分条件充分不必要条件必要条件必要不充分条件充分条件必要条件充要条件 在下列电路图中,表示开关A闭合是灯泡B亮的必要但不充分条件的线路图是( ).B【解析】开关A闭合,灯泡B不一定亮,灯泡B亮,开关A一定闭合.A 已知q是等比数列{an}的公比,则“q<1”是“数列{an}是递减数列”的 条件.?
【解析】由数列{an}是递减数列可得0
(1)p:∠A=∠B,q:∠A和∠B是对顶角.
(2)p:x=1,q:x2=1.
【解析】(1)∵p?/ q且q?p,∴p是q的必要不充分条件.
(2)∵q:x2=1?x=1或x=-1,∴x=1?x2=1,但x2=1?/ x=1,
∴p是q的充分不必要条件.必要不充分充分条件、必要条件、充要条件的判断
分析下面的各组命题中p是q的什么条件.(从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一个)
(1)在△ABC中,p:∠A=∠B,q:sin A=sin B.
(2)非空集合A、B中,p:x∈A∪B,q:x∈B.【解析】(1)在△ABC中,∠A=∠B?sin A=sin B,反之,若sin A=sin B,因为A与B不可能互补(因为三角形三个内角和为180°),所以只有A=B.故p是q的充要条件.
(2)显然x∈A∪B不一定有x∈B,但x∈B一定有x∈A∪B,所以p是q的必要不充分条件.7根据充分条件、必要条件求参数的取值范围
已知p:A={x∈R|x2+ax+1≤0},q:B={x∈R|x2-3x+2≤0},若p是q的充分不必要条件,求实数a的取值范围.充要条件的探求与证明
已知方程x2+(2k-1)x+k2=0,求使方程有两个大于1的根的充要条件.[问题]使方程有两个大于1的根的充要条件是k<-1吗? 已知命题p:1-c
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【解析】由A?B,得A∩B=A;反过来,由A∩B=A,且(A∩B)?B,得A?B.因此,“A?B”是“A∩B=A成立”的充要条件.2.已知平面α,β,直线m?平面α,则“平面α∥平面β”是“直线m∥平面β”的( ).
A.充分不必要条件 B.充要条件
C.必要不充分条件 D.既不充分也不必要条件
【解析】因为平面α∥平面β且直线m?平面α,所以直线m∥平面β,反之,当直线m∥平面β时,直线m?平面α,也可能平面α和平面β相交. A
3.设有如下三个命题:
甲: m∩l=A,m,l?α,m,l?β;
乙:直线m,l中至少有一条与平面β相交;
丙:平面α与平面β相交.
当甲成立时,乙是丙的 条件.?
【解析】由题意乙?丙,丙?乙.
故当甲成立时,乙是丙的充要条件.充要
