2018年高中数学第1章立体几何初步1.2.1平面的基本性质课件3苏教版必修2(34张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.1平面的基本性质课件3苏教版必修2(34张) |

|
|
| 格式 | zip | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:19:16 | ||
图片预览








文档简介
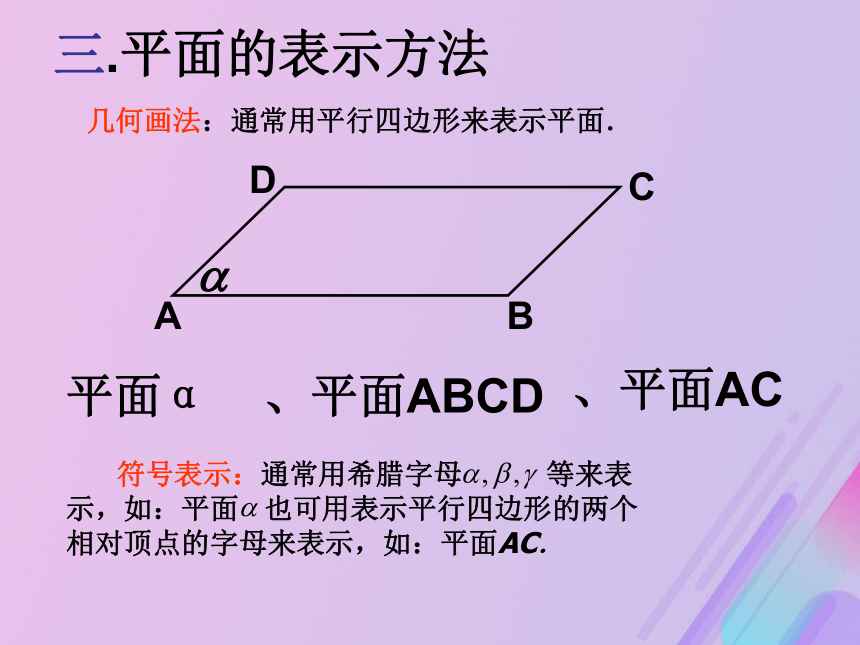
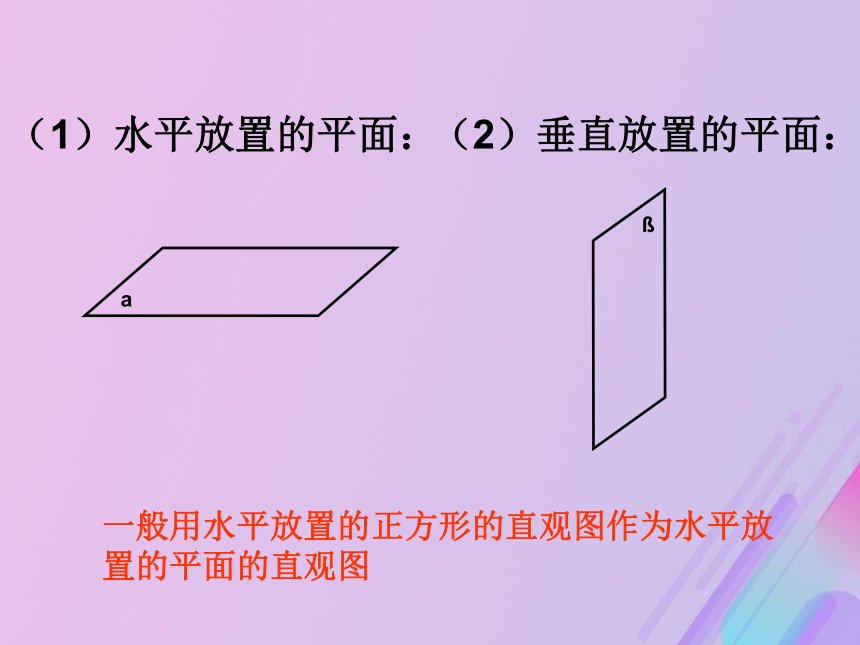
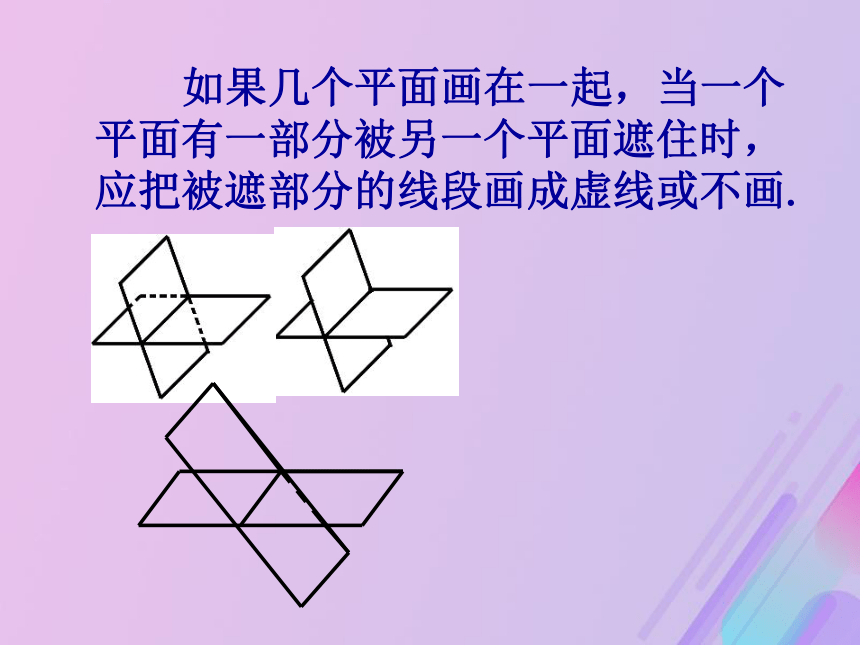
课件34张PPT。平面的基本性质(1) 象这些桌面、平静的湖面、镜面、黑板面等都给我们以____的印象一.平面的概念: 光滑的桌面、平静的湖面等都是我们很熟悉.二.平面的特征: 平面没有大小、厚薄和宽窄,平面在空间是无限延伸的。数学中的平面概念是现实平面加以抽象的结果。平面 平面是不加定义的基本概念,平面没有厚薄,它向四周无限延展.几何里的平面的特征:1.无限延展2.不计大小3.不计厚薄没有边界无所谓面积没有质量ADCB平面α、平面ABCD三.平面的表示方法几何画法:通常用平行四边形来表示平面. 符号表示:通常用希腊字母 等来表示,如:平面 也可用表示平行四边形的两个相对顶点的字母来表示,如:平面AC.、平面AC(1)水平放置的平面:(2)垂直放置的平面:一般用水平放置的正方形的直观图作为水平放置的平面的直观图 在画平行四边形表示平面时,所表示的平面如果是水平平面,通常把锐角画成45°,横边画成邻边的两倍.如果是非水平平面,只要画成平行四边形.45°铅直平面 如果几个平面画在一起,当一个平面有一部分被另一个平面遮住时,应把被遮部分的线段画成虚线或不画.【例1】已知命题:
①10个平面重叠起来,要比5个平面
重叠起来厚;
②有一个平面的长是50m,宽是20m;
③黑板面是平面;
④平面是绝对的平,没有大小、没有
厚度,可以无限延展的抽象的数学
概念.
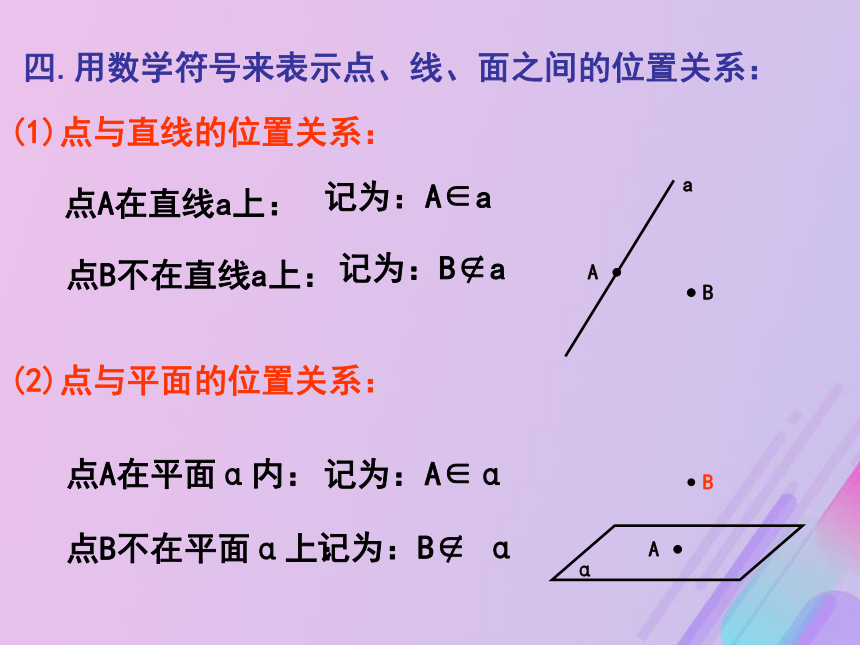
其中正确的的命题是__________.④四.用数学符号来表示点、线、面之间的位置关系: 点A在直线a上:记为:A∈a点B不在直线a上: 点A在平面α内:记为:A∈α点B不在平面α上:(1)点与直线的位置关系:(2)点与平面的位置关系:如果把桌面看作一个平面,把你的笔看作
是一条直线的话,你觉得在什么情况下,
才能使你的笔所代表的直线上所有的点都
能在桌面上?
思考:··直线AB与直线BC相交记为:AB∩BC=B直线AB在平面α内记为:AB 平面α直线AB不在平面α内记为:AB 平面α点A在直线l上点A在直线l外点A在平面 内点A在平面 外直线l在平面 外直线l在平面 内公理1.如果一条直线上两点在一个平面内,那么这条直线上的所有的点都在这个平面内(即直线在平面内)。观察下列问题,你能得到什么结论?五.平面的基本性质公理1.如果一条直线上两点在一个平面内,那么这条直线上的所有的点都在这个平面内(即直线在平面内)。文字语言:图形语言:符号语言:一是可以用来判定一条直线是否在平面内,即
要判定直线在平面内,只需确定直线上两个
点在平面内即可; 二是可以用来判定点在平面内,即如果直线在
平面内、点在直线上,则点在平面内. 三是表明平面是“平的”公理1的作用有三:【例2】一条直线经过平面内一点与平面外一
点,它和这个平面有几个公共点?为
什么?解:这条直线和这个平面只有一个公共点.假设这条直线和这个平面有两个公共点根据公理1可得这条直线上所有的点都在这个平面内这条直线过平面外的一点也在这个平面内故:与已知矛盾所以这条直线与这个平面只有一个公共点.公理2.如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。观察下列问题,你能得到什么结论?天花板α墙面β墙面γ文字语言:图形语言:符号语言:公理2.如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。
一是判定两个平面相交,即如果两个平面有一个
公共点,那么这两个平面相交;二是判定点在直线上,即点若是某两个平面的公
共点,那么这点就在这两个平面的交线上.公理2的作用有二:证明:(公理2)同理可证:要证明空间诸点共线,通常证明这些点同时落在两个相交平面内,则落在它们的交线上. 用手指头将一本书平衡地摆方在空间某一位置,至少需要几个手指头?思考:这些手指需要满足什么条件?公理3.过不在同一直线上的三点,有且只有一个平面.观察下列问题,你能得到什么结论_?有且只有门文字语言:图形语言:符号语言:公理3.过不在同一直线上的三点,有且只有一个平面.或记为平面ABC公理3是确定平面的依据. 练习【例4】为什么用两个合页和一把锁就可以固
定一扇门,有的自行车旁只安装一只
撑脚呢?因为不共线的三点可以确定一个平面.答:练习说明图形是存在的!说明图形是唯一的!“有”“只有一个”至少有一个至多有一个有且只有一个的含义:返回1.已知下列四个说法:①很平的桌面是一个平面
②平面ABCD的面积为10cm2
③平面是矩形或平行四边形
④空间图形中,后引的辅助线是虚线
其中正确的命题有
A.0个 B.1个 C.2个 D.3个 练习(×)(×)(×)(×)3.正方体的各顶点如图所示,正方体的三个面所在平面 ,分别记作 ,试用适当的符号填空. 4.根据下列符号表示的语句,说出有关点、线、面的关系,并画出图形.点A在直线l上点A在直线l外点A在平面 内点A在平面 外直线l在平面 外直线l在平面 内5填空想一想:两个平面能将空间分成几部分?3 或 4三个平面能将空间分成几部分?678
①10个平面重叠起来,要比5个平面
重叠起来厚;
②有一个平面的长是50m,宽是20m;
③黑板面是平面;
④平面是绝对的平,没有大小、没有
厚度,可以无限延展的抽象的数学
概念.
其中正确的的命题是__________.④四.用数学符号来表示点、线、面之间的位置关系: 点A在直线a上:记为:A∈a点B不在直线a上: 点A在平面α内:记为:A∈α点B不在平面α上:(1)点与直线的位置关系:(2)点与平面的位置关系:如果把桌面看作一个平面,把你的笔看作
是一条直线的话,你觉得在什么情况下,
才能使你的笔所代表的直线上所有的点都
能在桌面上?
思考:··直线AB与直线BC相交记为:AB∩BC=B直线AB在平面α内记为:AB 平面α直线AB不在平面α内记为:AB 平面α点A在直线l上点A在直线l外点A在平面 内点A在平面 外直线l在平面 外直线l在平面 内公理1.如果一条直线上两点在一个平面内,那么这条直线上的所有的点都在这个平面内(即直线在平面内)。观察下列问题,你能得到什么结论?五.平面的基本性质公理1.如果一条直线上两点在一个平面内,那么这条直线上的所有的点都在这个平面内(即直线在平面内)。文字语言:图形语言:符号语言:一是可以用来判定一条直线是否在平面内,即
要判定直线在平面内,只需确定直线上两个
点在平面内即可; 二是可以用来判定点在平面内,即如果直线在
平面内、点在直线上,则点在平面内. 三是表明平面是“平的”公理1的作用有三:【例2】一条直线经过平面内一点与平面外一
点,它和这个平面有几个公共点?为
什么?解:这条直线和这个平面只有一个公共点.假设这条直线和这个平面有两个公共点根据公理1可得这条直线上所有的点都在这个平面内这条直线过平面外的一点也在这个平面内故:与已知矛盾所以这条直线与这个平面只有一个公共点.公理2.如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。观察下列问题,你能得到什么结论?天花板α墙面β墙面γ文字语言:图形语言:符号语言:公理2.如果两个平面有一个公共点,那么它们还有其它公共点,这些公共点的集合是经过这个公共点的一条直线。
一是判定两个平面相交,即如果两个平面有一个
公共点,那么这两个平面相交;二是判定点在直线上,即点若是某两个平面的公
共点,那么这点就在这两个平面的交线上.公理2的作用有二:证明:(公理2)同理可证:要证明空间诸点共线,通常证明这些点同时落在两个相交平面内,则落在它们的交线上. 用手指头将一本书平衡地摆方在空间某一位置,至少需要几个手指头?思考:这些手指需要满足什么条件?公理3.过不在同一直线上的三点,有且只有一个平面.观察下列问题,你能得到什么结论_?有且只有门文字语言:图形语言:符号语言:公理3.过不在同一直线上的三点,有且只有一个平面.或记为平面ABC公理3是确定平面的依据. 练习【例4】为什么用两个合页和一把锁就可以固
定一扇门,有的自行车旁只安装一只
撑脚呢?因为不共线的三点可以确定一个平面.答:练习说明图形是存在的!说明图形是唯一的!“有”“只有一个”至少有一个至多有一个有且只有一个的含义:返回1.已知下列四个说法:①很平的桌面是一个平面
②平面ABCD的面积为10cm2
③平面是矩形或平行四边形
④空间图形中,后引的辅助线是虚线
其中正确的命题有
A.0个 B.1个 C.2个 D.3个 练习(×)(×)(×)(×)3.正方体的各顶点如图所示,正方体的三个面所在平面 ,分别记作 ,试用适当的符号填空. 4.根据下列符号表示的语句,说出有关点、线、面的关系,并画出图形.点A在直线l上点A在直线l外点A在平面 内点A在平面 外直线l在平面 外直线l在平面 内5填空想一想:两个平面能将空间分成几部分?3 或 4三个平面能将空间分成几部分?678
