2018年高中数学第1章立体几何初步1.2.4平面与平面的位置关系课件5苏教版必修2(16张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.4平面与平面的位置关系课件5苏教版必修2(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:27:32 | ||
图片预览





文档简介
课件16张PPT。平面与平面的位置关系
(第一课时) 如果平面外一条直线和这个平面内的一条直线平行,则该直线与这个平面平行.图形语言符号语言前置性补偿
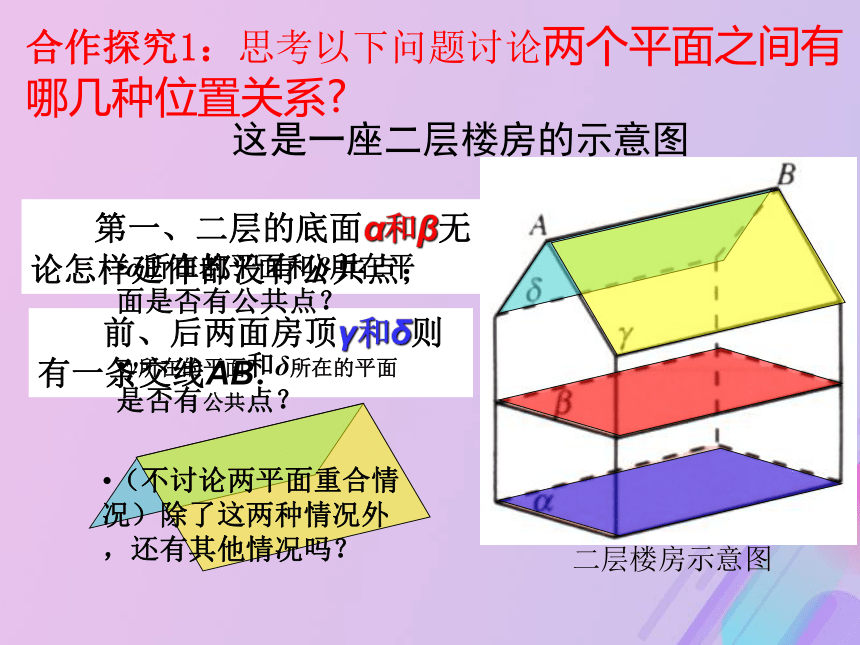
(1)直线与平面之间的位置关系 (2)直线与平面平行的判定定理二层楼房示意图 第一、二层的底面α和β无论怎样延伸都没有公共点; 前、后两面房顶γ和δ则有一条交线AB.这是一座二层楼房的示意图α所在的平面和β所在平面是否有公共点?γ所在的平面和δ所在的平面是否有公共点?(不讨论两平面重合情况)除了这两种情况外,还有其他情况吗?合作探究1:思考以下问题讨论两个平面之间有哪几种位置关系?两个平面的位置关系有:没有公共点有一条公共直线∥新知1新知2 如果两个平面没有公共点,那么就说这两个平面互相平行两个平面平行的定义1.两个平面满足什么条件才能够平行呢?2.有没有学过两平面平行的判定?学过什么平
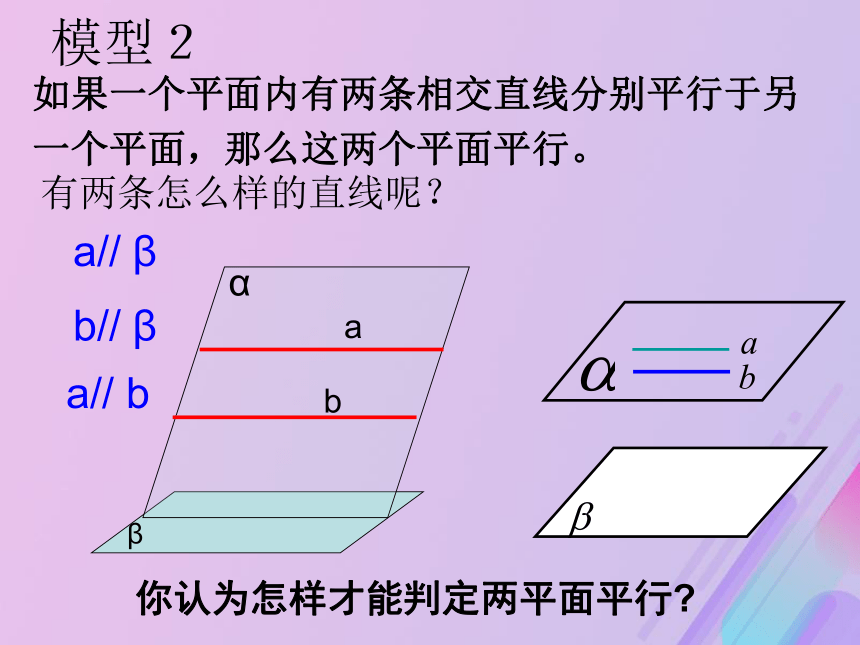
行关系?3.如果平面α内有一条直线a平行于平面β那么α与β平行吗?4.如果平面α内有两条直线a,b平行于平面β那么α与β平行吗?合作探究2:带着下面几个问题讨论怎样判定平面与平面平行,这些条件到底够不够? 模型1αβa// βααα模型2有两条怎么样的直线呢?a// βabαb// ββa// b如果一个平面内有两条相交直线分别平行于另
一个平面,那么这两个平面平行。你认为怎样才能判定两平面平行?新知3:平面与平面平行的判定定理: 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.简述为:线面平行?面面平行? //β线不在多,重在相交 你知道木匠师傅是怎
样用水平仪来检测桌面是
否水平的?水平面练习:判断下列命题是否正确:
( )1、如果一个平面内有两条直线平行于另一个平面,
那么这两个平面平行;
( ) 2、如果一个平面内有两条不平行的直线都平行
于另一个平面,那么这两个平面平行;
( )3、如果一个平面内有无数条直线分别平行于另
一个平面,那么这两个平面平行;
( )4、如果一个平面内任意一条直线都平行于另一
个平面,那么这两个平面平行. 证明:长方体ABCD-A1B1C1D1 中, D1C1∥A1B1,D1C1=A1B1又 A1B1∥AB ,A1B1=AB∴ D1C1∥AB,D1C1=AB∴ D1A ∥平面C1BD典型例题
【例题】已知长方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面C1BD∴ D1A∥ C1B∴ 四边形D1C1BA为平行四边形∴ 平面AB1D1 ∥平面C1BD证明线线平行证明线面平行证明面面平行同理 D1B1∥平面C1BD 又D1A ∩D1B1=D1
1、证明线面平行时,注意有三个条件解题反思:2、证明面面平行时,注意条件是线面平行,
而不是线线平行3、证明面面平行时,转化成证明线面平行,
而证明线面平行,又转化成证明线线平行4、证明面面平行时,有5个条件,缺一不可.变式1、已知正方体ABCD-A1B1C1D1,
P,Q, R,分别为A1A,AB,AD的中点
求证:平面PQR∥平面CB1D1.分析:连结A1B,
PQ∥ A1B
A1B ∥CD1
故PQ∥CD1
同理可得,……变式2:已知正方体ABCD-A1B1C1D1,设M、N、E、F分别为棱A1B1、A1D1、 C1D1、 B1C1的中点.求证:面AMN∥面EFBD.MNEF2.应用判定定理判定面面平行时应注意:
两条相交直线课堂小结:通过本节课学习,你有哪些收获?
1.平面与平面平行的判定:3.应用判定定理判定面面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。
(1)直线与平面之间的位置关系 (2)直线与平面平行的判定定理二层楼房示意图 第一、二层的底面α和β无论怎样延伸都没有公共点; 前、后两面房顶γ和δ则有一条交线AB.这是一座二层楼房的示意图α所在的平面和β所在平面是否有公共点?γ所在的平面和δ所在的平面是否有公共点?(不讨论两平面重合情况)除了这两种情况外,还有其他情况吗?合作探究1:思考以下问题讨论两个平面之间有哪几种位置关系?两个平面的位置关系有:没有公共点有一条公共直线∥新知1新知2 如果两个平面没有公共点,那么就说这两个平面互相平行两个平面平行的定义1.两个平面满足什么条件才能够平行呢?2.有没有学过两平面平行的判定?学过什么平
行关系?3.如果平面α内有一条直线a平行于平面β那么α与β平行吗?4.如果平面α内有两条直线a,b平行于平面β那么α与β平行吗?合作探究2:带着下面几个问题讨论怎样判定平面与平面平行,这些条件到底够不够? 模型1αβa// βααα模型2有两条怎么样的直线呢?a// βabαb// ββa// b如果一个平面内有两条相交直线分别平行于另
一个平面,那么这两个平面平行。你认为怎样才能判定两平面平行?新知3:平面与平面平行的判定定理: 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.简述为:线面平行?面面平行? //β线不在多,重在相交 你知道木匠师傅是怎
样用水平仪来检测桌面是
否水平的?水平面练习:判断下列命题是否正确:
( )1、如果一个平面内有两条直线平行于另一个平面,
那么这两个平面平行;
( ) 2、如果一个平面内有两条不平行的直线都平行
于另一个平面,那么这两个平面平行;
( )3、如果一个平面内有无数条直线分别平行于另
一个平面,那么这两个平面平行;
( )4、如果一个平面内任意一条直线都平行于另一
个平面,那么这两个平面平行. 证明:长方体ABCD-A1B1C1D1 中, D1C1∥A1B1,D1C1=A1B1又 A1B1∥AB ,A1B1=AB∴ D1C1∥AB,D1C1=AB∴ D1A ∥平面C1BD典型例题
【例题】已知长方体ABCD-A1B1C1D1,求证:平面AB1D1∥平面C1BD∴ D1A∥ C1B∴ 四边形D1C1BA为平行四边形∴ 平面AB1D1 ∥平面C1BD证明线线平行证明线面平行证明面面平行同理 D1B1∥平面C1BD 又D1A ∩D1B1=D1
1、证明线面平行时,注意有三个条件解题反思:2、证明面面平行时,注意条件是线面平行,
而不是线线平行3、证明面面平行时,转化成证明线面平行,
而证明线面平行,又转化成证明线线平行4、证明面面平行时,有5个条件,缺一不可.变式1、已知正方体ABCD-A1B1C1D1,
P,Q, R,分别为A1A,AB,AD的中点
求证:平面PQR∥平面CB1D1.分析:连结A1B,
PQ∥ A1B
A1B ∥CD1
故PQ∥CD1
同理可得,……变式2:已知正方体ABCD-A1B1C1D1,设M、N、E、F分别为棱A1B1、A1D1、 C1D1、 B1C1的中点.求证:面AMN∥面EFBD.MNEF2.应用判定定理判定面面平行时应注意:
两条相交直线课堂小结:通过本节课学习,你有哪些收获?
1.平面与平面平行的判定:3.应用判定定理判定面面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系。
