2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件4苏教版必修2(16张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件4苏教版必修2(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:29:22 | ||
图片预览






文档简介
课件16张PPT。 直 线 的 斜 率
笛卡尔终身保持着在耶稣会学校读书期间养成的“晨思”习惯,他在一次“晨思”时,看见一只苍蝇在天花板上爬,他突然想到,如果知道了苍蝇与相邻两个墙壁的距离之间的关系,就能描述它的路线,这是他产生了关于解析几何的最初闪念。x笛卡尔法国数学家(1596-1650)
解析几何学的创立者 几何学是研究现实世界中物体的形状、大小与位置关系的数学学科。
解析几何是17世纪数学发展的重大成果之一,其本质是用代数方法研究图形的几何性质,体现了数形结合的重要数学思想。
解析几何简介:解析几何的本质用代数的方法研究
几何性质平面直角坐标系费马(1601-1665)
法国著名数学家
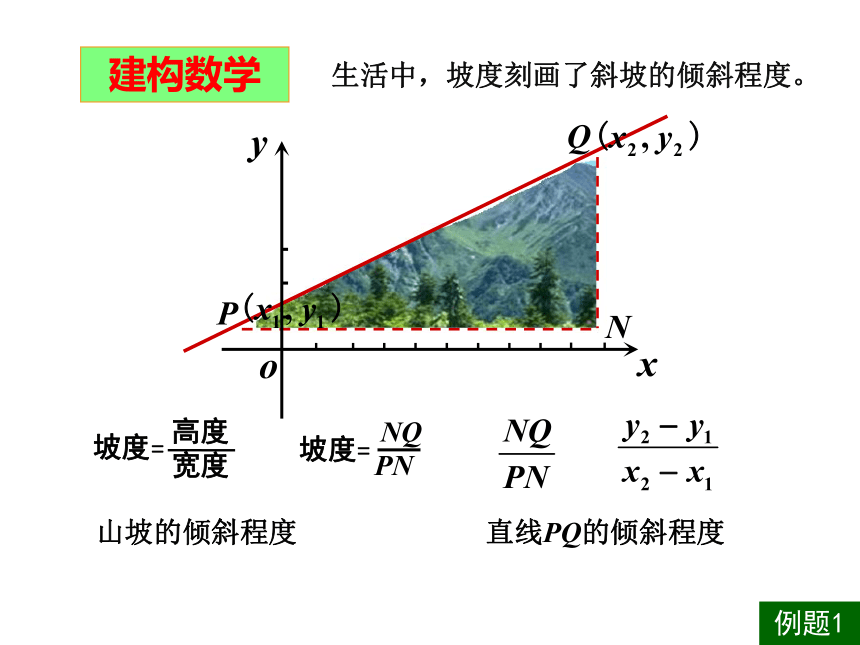
“业余数学家之王”一点和一个确定的方向可以确定一条直线.如何确定直线的方向?情境引入:灰太狼爬的山坡更陡(倾斜程度更大)坡度=高度宽度坡度越大,山坡越陡.建构数学PQN生活中,坡度刻画了斜坡的倾斜程度。例题1山坡的倾斜程度直线PQ的倾斜程度已知:对数式lg(k1·k2)有意义,其中k1 , k2为直线l1, l2的斜率,则下列图象中能表示直线l1, l2的序号为___________(1)课堂练习:说出下列直线的斜率根据下列条件,分别画出过点P ,且斜率为k的直线:例题2(1)直线的斜率是定值吗?(2)如果KAB=KAC,那么A,B,C三点有什么关系?在同一直线上取不同的点计算斜率,相等吗?直线的斜率是定值探究活动如果KAB=KBC,那么A,B,C三点共线.三点A(1,-1), B(3,3), C(5,a)在一条直线上,求a的值.判断多点共线的方法:(1)共点的直线斜率相等
(2)共起点的向量共线.(或者均垂直于x轴) ;思考题核心知识
方法
思想直线的斜率小结提高类比坐标系下:代数方法研究几何问题课后探究 斜率是刻画直线倾斜程度的量,斜率的大小跟直线的倾斜程度有什么关系?
能否找到其他刻画直线倾斜程度的量,如果有,请找出它跟直线的斜率之间的联系与区别.想一 想已知直线 l 经过点A(m,2),B(1,m2+2),试求直线 l 的斜率.解 当m≠1时,当m=1时,直线AB垂直于x轴,所以斜率不存在.友情提醒:考虑直线的斜率是否存在例题3根据下列条件,分别画出过点P ,且斜率为k的直线:例题2解:(1)根据斜率为3/4表示直线上的任意一点沿x轴方向向右平移4个单位,再沿y轴方向向上平移3个单位后仍在此直线上. 如果我们从点(0,0)开始,向右平移4个单位,再向上平移3个单位,就得到点(4,3).因此,通过点(4,3)和点(3,2)画直线,即为所求. 斜率 (2)由于 ,因此,将点(3,2)向右平移5个单位,再向下平移4个单位,得到(8,-2).通过点(8,-2)和点(3,2)画直线,即为所求.
笛卡尔终身保持着在耶稣会学校读书期间养成的“晨思”习惯,他在一次“晨思”时,看见一只苍蝇在天花板上爬,他突然想到,如果知道了苍蝇与相邻两个墙壁的距离之间的关系,就能描述它的路线,这是他产生了关于解析几何的最初闪念。x笛卡尔法国数学家(1596-1650)
解析几何学的创立者 几何学是研究现实世界中物体的形状、大小与位置关系的数学学科。
解析几何是17世纪数学发展的重大成果之一,其本质是用代数方法研究图形的几何性质,体现了数形结合的重要数学思想。
解析几何简介:解析几何的本质用代数的方法研究
几何性质平面直角坐标系费马(1601-1665)
法国著名数学家
“业余数学家之王”一点和一个确定的方向可以确定一条直线.如何确定直线的方向?情境引入:灰太狼爬的山坡更陡(倾斜程度更大)坡度=高度宽度坡度越大,山坡越陡.建构数学PQN生活中,坡度刻画了斜坡的倾斜程度。例题1山坡的倾斜程度直线PQ的倾斜程度已知:对数式lg(k1·k2)有意义,其中k1 , k2为直线l1, l2的斜率,则下列图象中能表示直线l1, l2的序号为___________(1)课堂练习:说出下列直线的斜率根据下列条件,分别画出过点P ,且斜率为k的直线:例题2(1)直线的斜率是定值吗?(2)如果KAB=KAC,那么A,B,C三点有什么关系?在同一直线上取不同的点计算斜率,相等吗?直线的斜率是定值探究活动如果KAB=KBC,那么A,B,C三点共线.三点A(1,-1), B(3,3), C(5,a)在一条直线上,求a的值.判断多点共线的方法:(1)共点的直线斜率相等
(2)共起点的向量共线.(或者均垂直于x轴) ;思考题核心知识
方法
思想直线的斜率小结提高类比坐标系下:代数方法研究几何问题课后探究 斜率是刻画直线倾斜程度的量,斜率的大小跟直线的倾斜程度有什么关系?
能否找到其他刻画直线倾斜程度的量,如果有,请找出它跟直线的斜率之间的联系与区别.想一 想已知直线 l 经过点A(m,2),B(1,m2+2),试求直线 l 的斜率.解 当m≠1时,当m=1时,直线AB垂直于x轴,所以斜率不存在.友情提醒:考虑直线的斜率是否存在例题3根据下列条件,分别画出过点P ,且斜率为k的直线:例题2解:(1)根据斜率为3/4表示直线上的任意一点沿x轴方向向右平移4个单位,再沿y轴方向向上平移3个单位后仍在此直线上. 如果我们从点(0,0)开始,向右平移4个单位,再向上平移3个单位,就得到点(4,3).因此,通过点(4,3)和点(3,2)画直线,即为所求. 斜率 (2)由于 ,因此,将点(3,2)向右平移5个单位,再向下平移4个单位,得到(8,-2).通过点(8,-2)和点(3,2)画直线,即为所求.
