2018年高中数学第2章平面解析几何初步2.1.2直线的方程课件4苏教版必修2(16张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.2直线的方程课件4苏教版必修2(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 324.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:29:43 | ||
图片预览






文档简介
课件16张PPT。2.1.2直线的方程
——点斜式、斜截式 问题一:所有直线都有倾斜角和斜率吗?倾斜角的范围是什么?
问题二:如何求一条直线的斜率?
提出问题:一、温故探新
1.温故:直线斜率公式的运用.
(1)已知:直线l经过点A(2,3),B(1,4),请计算直线l的斜率;
(2)已知:直线l经过点A(m,3),B(1,4)且斜率为-3,请计算m的值;
(3)直线l经过点A(1,3),斜率为2,点P(-1,-1)在直线l上吗?深入探究:问题四:在直角坐标系内,已知直线l上一点P0 (x0,y0)和它的斜率k,你能画出这条直线吗?问题三:在直角坐标系内,已知直线l上一P0(x0,y0)和它的斜率k,这条直线上其它的点P(x,y)的坐标x,y与k,x0,y0之间存在一个关系式吗?
2.探新:
(4)已知:直线l经过点A(-1,3)且斜率为-2,你能求出l经过的另一点B(2,y)的纵坐标吗? 你能画出直线吗?
(5)已知直线l经过点A(-1,3) ,斜率为-2,点P (x,y)在直线l上运动,那么点P的坐标(x,y)会满足什么式子呢?你能画出这条直线吗?
直线l经过点 P0(x0,y0)且斜率为k,设点P(x,y)是直线l上的任意一点,则x,y与k,x0,y0之间存在一个关系式并且根据这个关系式可以求出其他点的坐标,画出这条直线.
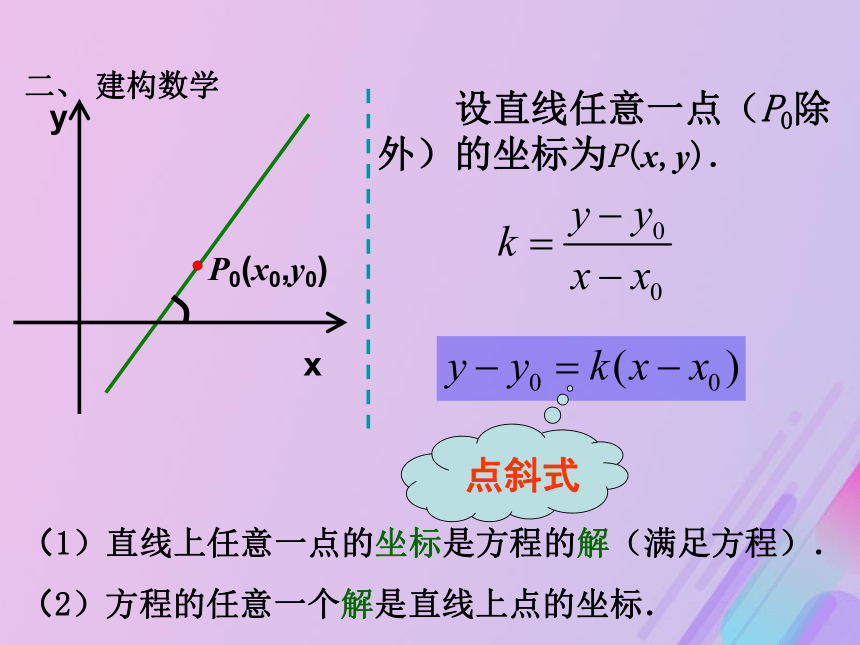
结论:由直线上一点和它的斜率可以确定这条直线.探究结论:二、 建构数学xy(1)直线上任意一点的坐标是方程的解(满足方程).P0(x0,y0) 设直线任意一点(P0除外)的坐标为P(x,y).(2)方程的任意一个解是直线上点的坐标.点斜式(1)当直线l的倾斜角是00时,tan00=0,即k=0,这时直线l与x轴平行或重合.l的方程:y-y1=0 或 y=y1(2)当直线l的倾斜角是900时,直线l没有斜率,这时直线l与y轴平行或重合.l的方程:x-x1=0 或 x=x1(3)已知直线l的斜率为k,它与y轴的交点是P(0,b),求直线l的方程.
注:直线与x轴交点为(a,0),与y轴交点为(0,b),则称a为直线在x轴上的截距,b为直线在y轴上的截距(截距可以大于0,也可以等于0或小于0,截距与距离是二个不同的概念)
xyP0(0,b) 设直线经过点P0(0, b),其斜率为k,求直线方程.斜截式斜率截距当知道斜率和截距时用斜截式.斜截式方程: y = k x + b
几何意义:k 是直线的斜率,b是直线在y轴上的
截距.
对斜截式方程的探究:
探究一:截距是不是距离?是不是一定要为正?
探究二:直线斜截式方程与一次函数关系是什么?
三、数学应用
例1 已知一条直线经过点P(-2,3),斜率为2,求这条直线方程.
例2 求直线 的倾斜角.
例3 求直线 绕点(2,0)按顺时针方向旋转30°所得的直线方程.
练习1 写出下列直线的点斜式方程:练习 2 说出下列点斜式方程所对应的直线斜率和倾斜角:练习3 当k不断变化时,直线y= k(x+2) 恒过点 .
练习4 已知直线l的方程为 ,
点P的坐标为(1,-1);
(1) 求经过点P且与直线l斜率相等的直线方程;
(2) 求经过点P且倾斜角为直线l的倾斜角2倍的直线
方程.
练习5 求在x轴上的截距为1,且倾斜角的正弦值为
的直线方程. 练习6 根据下列条件,直接写出直线的方程:
(1)斜率为-2,在y轴上的截距为-2 ;
(2)斜率为 ,在x轴上的截距为-7.小结:1.点斜式方程:当知道斜率和一点坐标时用点斜式.2.斜截式方程:当知道斜率k和截距b时用斜截式.3.特殊情况:①直线与x轴平行或重合时,倾斜角α=0°②直线与y轴平行或重合时,倾斜角α=90°
问题二:如何求一条直线的斜率?
提出问题:一、温故探新
1.温故:直线斜率公式的运用.
(1)已知:直线l经过点A(2,3),B(1,4),请计算直线l的斜率;
(2)已知:直线l经过点A(m,3),B(1,4)且斜率为-3,请计算m的值;
(3)直线l经过点A(1,3),斜率为2,点P(-1,-1)在直线l上吗?深入探究:问题四:在直角坐标系内,已知直线l上一点P0 (x0,y0)和它的斜率k,你能画出这条直线吗?问题三:在直角坐标系内,已知直线l上一P0(x0,y0)和它的斜率k,这条直线上其它的点P(x,y)的坐标x,y与k,x0,y0之间存在一个关系式吗?
2.探新:
(4)已知:直线l经过点A(-1,3)且斜率为-2,你能求出l经过的另一点B(2,y)的纵坐标吗? 你能画出直线吗?
(5)已知直线l经过点A(-1,3) ,斜率为-2,点P (x,y)在直线l上运动,那么点P的坐标(x,y)会满足什么式子呢?你能画出这条直线吗?
直线l经过点 P0(x0,y0)且斜率为k,设点P(x,y)是直线l上的任意一点,则x,y与k,x0,y0之间存在一个关系式并且根据这个关系式可以求出其他点的坐标,画出这条直线.
结论:由直线上一点和它的斜率可以确定这条直线.探究结论:二、 建构数学xy(1)直线上任意一点的坐标是方程的解(满足方程).P0(x0,y0) 设直线任意一点(P0除外)的坐标为P(x,y).(2)方程的任意一个解是直线上点的坐标.点斜式(1)当直线l的倾斜角是00时,tan00=0,即k=0,这时直线l与x轴平行或重合.l的方程:y-y1=0 或 y=y1(2)当直线l的倾斜角是900时,直线l没有斜率,这时直线l与y轴平行或重合.l的方程:x-x1=0 或 x=x1(3)已知直线l的斜率为k,它与y轴的交点是P(0,b),求直线l的方程.
注:直线与x轴交点为(a,0),与y轴交点为(0,b),则称a为直线在x轴上的截距,b为直线在y轴上的截距(截距可以大于0,也可以等于0或小于0,截距与距离是二个不同的概念)
xyP0(0,b) 设直线经过点P0(0, b),其斜率为k,求直线方程.斜截式斜率截距当知道斜率和截距时用斜截式.斜截式方程: y = k x + b
几何意义:k 是直线的斜率,b是直线在y轴上的
截距.
对斜截式方程的探究:
探究一:截距是不是距离?是不是一定要为正?
探究二:直线斜截式方程与一次函数关系是什么?
三、数学应用
例1 已知一条直线经过点P(-2,3),斜率为2,求这条直线方程.
例2 求直线 的倾斜角.
例3 求直线 绕点(2,0)按顺时针方向旋转30°所得的直线方程.
练习1 写出下列直线的点斜式方程:练习 2 说出下列点斜式方程所对应的直线斜率和倾斜角:练习3 当k不断变化时,直线y= k(x+2) 恒过点 .
练习4 已知直线l的方程为 ,
点P的坐标为(1,-1);
(1) 求经过点P且与直线l斜率相等的直线方程;
(2) 求经过点P且倾斜角为直线l的倾斜角2倍的直线
方程.
练习5 求在x轴上的截距为1,且倾斜角的正弦值为
的直线方程. 练习6 根据下列条件,直接写出直线的方程:
(1)斜率为-2,在y轴上的截距为-2 ;
(2)斜率为 ,在x轴上的截距为-7.小结:1.点斜式方程:当知道斜率和一点坐标时用点斜式.2.斜截式方程:当知道斜率k和截距b时用斜截式.3.特殊情况:①直线与x轴平行或重合时,倾斜角α=0°②直线与y轴平行或重合时,倾斜角α=90°
