2018年高中数学第2章平面解析几何初步2.1.4两条直线的交点课件6苏教版必修2(17张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.4两条直线的交点课件6苏教版必修2(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 481.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:31:07 | ||
图片预览





文档简介
课件17张PPT。2.1.4 两条直线的交点复习回顾2.利用两直线的一般式方程判断两直线的平行与垂直关系.
l1:A1x+B1y+C1=0
l2:A2x+B2y+C2=0
l1∥l2 ? A1B2 = A2B1,且A1C2≠A2C1或 B1C2≠B2C1.
l1⊥l2 ? A1A2+B1B2=0.1.平面内两直线的位置关系.
相交(有且只有一个公共点)
平行(无公共点)
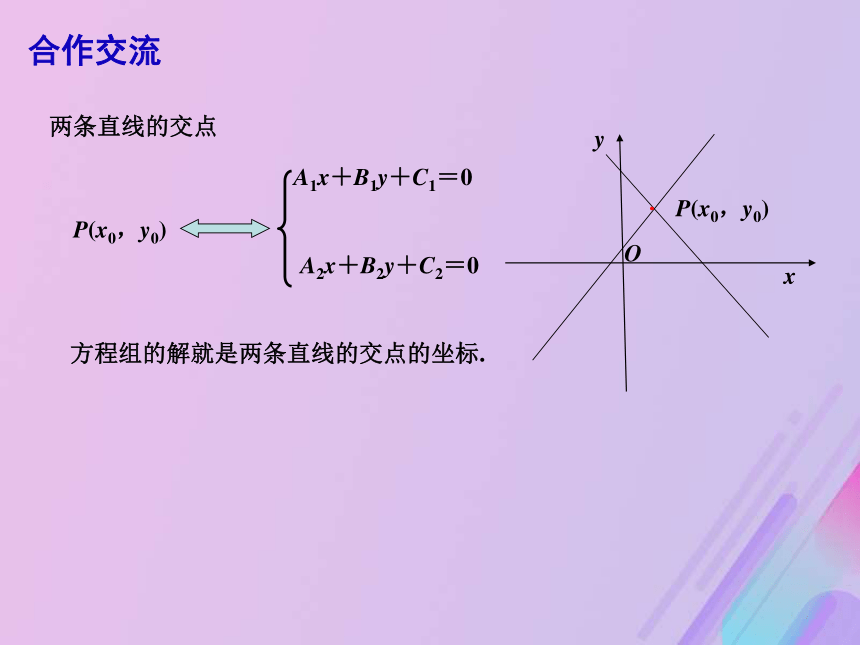
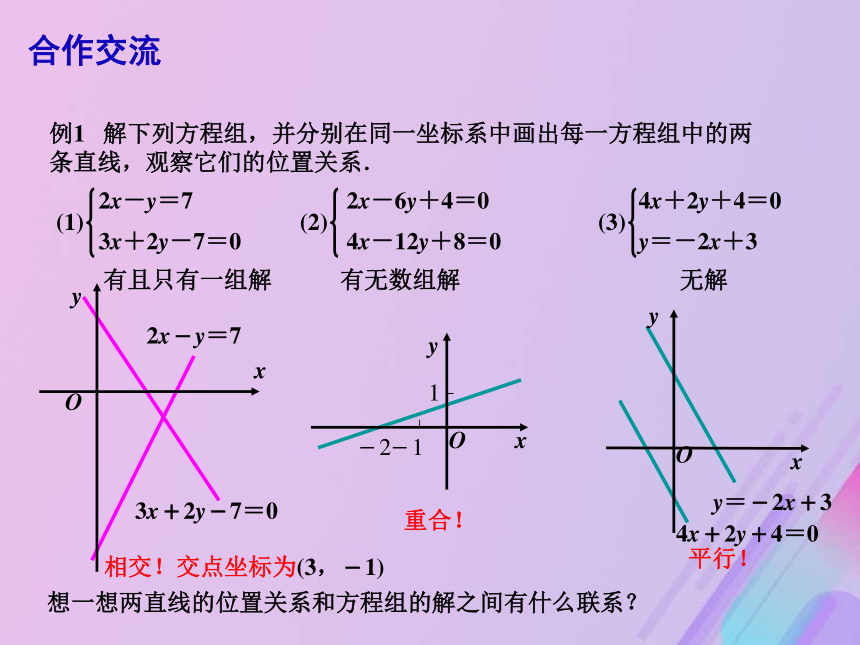
重合(有无数个公共点)直线x+y-2=0与直线x-y=0的位置关系是什么? 问题情境垂足的坐标能否求出?如何求? 请试着总结求两条直线交点的一般方法.P(x0,y0).xyOP(x0,y0)A1x+B1y+C1=0A2x+B2y+C2=0方程组的解就是两条直线的交点的坐标.合作交流两条直线的交点想一想两直线的位置关系和方程组的解之间有什么联系?例1 解下列方程组,并分别在同一坐标系中画出每一方程组中的两条直线,观察它们的位置关系.(1)2x-y=73x+2y-7=0(2)2x-6y+4=04x-12y+8=0(3)4x+2y+4=0y=-2x+3 3x+2y-7=02x-y=7有无数组解有且只有一组解无解y=-2x+34x+2y+4=0平行!相交!交点坐标为(3,-1)重合!合作交流设两条直线的方程分别是数学原理例2 直线l经过原点,且经过另两条直线
2x+3y+8=0,x-y-1=0的交点,求直线l的方程. 合作交流??合作交流??该方程表示什么图形???该图形有何特点探究拓展=0时,方程为2x+3y+8=0xy=1时,方程为3x+2y+7=0l2=-1时,方程为x+4y+9=00l1l3-2-1发现:此方程表示经过直线2x+3y+8=0与直线x-y-1=0交点的直线系(直线集合)?探究拓展 不包含直线l2探究拓展??反思:
方法(1)普通方法 求交点,求斜率.利用点斜式写出方程 方法(2)利用直线系方程??合作交流??分析:化为过两直线交点的直线系方程.合作交流合作交流例5 已知两条直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
求m为何值时,两条直线:(1)相交; (2)垂直;(3)平行;(4)重合. 合作交流知识与技能:
(1)通过解方程组确定两直线交点坐标.
(2)通过求交点坐标判断两直线的位置关系 .
(3)过定点的直线系方程的理解与应用.
思想与方法:
方程(组)思想、数形结合思想.小结反思:
l1:A1x+B1y+C1=0
l2:A2x+B2y+C2=0
l1∥l2 ? A1B2 = A2B1,且A1C2≠A2C1或 B1C2≠B2C1.
l1⊥l2 ? A1A2+B1B2=0.1.平面内两直线的位置关系.
相交(有且只有一个公共点)
平行(无公共点)
重合(有无数个公共点)直线x+y-2=0与直线x-y=0的位置关系是什么? 问题情境垂足的坐标能否求出?如何求? 请试着总结求两条直线交点的一般方法.P(x0,y0).xyOP(x0,y0)A1x+B1y+C1=0A2x+B2y+C2=0方程组的解就是两条直线的交点的坐标.合作交流两条直线的交点想一想两直线的位置关系和方程组的解之间有什么联系?例1 解下列方程组,并分别在同一坐标系中画出每一方程组中的两条直线,观察它们的位置关系.(1)2x-y=73x+2y-7=0(2)2x-6y+4=04x-12y+8=0(3)4x+2y+4=0y=-2x+3 3x+2y-7=02x-y=7有无数组解有且只有一组解无解y=-2x+34x+2y+4=0平行!相交!交点坐标为(3,-1)重合!合作交流设两条直线的方程分别是数学原理例2 直线l经过原点,且经过另两条直线
2x+3y+8=0,x-y-1=0的交点,求直线l的方程. 合作交流??合作交流??该方程表示什么图形???该图形有何特点探究拓展=0时,方程为2x+3y+8=0xy=1时,方程为3x+2y+7=0l2=-1时,方程为x+4y+9=00l1l3-2-1发现:此方程表示经过直线2x+3y+8=0与直线x-y-1=0交点的直线系(直线集合)?探究拓展 不包含直线l2探究拓展??反思:
方法(1)普通方法 求交点,求斜率.利用点斜式写出方程 方法(2)利用直线系方程??合作交流??分析:化为过两直线交点的直线系方程.合作交流合作交流例5 已知两条直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,
求m为何值时,两条直线:(1)相交; (2)垂直;(3)平行;(4)重合. 合作交流知识与技能:
(1)通过解方程组确定两直线交点坐标.
(2)通过求交点坐标判断两直线的位置关系 .
(3)过定点的直线系方程的理解与应用.
思想与方法:
方程(组)思想、数形结合思想.小结反思:
