2018年高中数学第2章平面解析几何初步2.1.5平面上两点间的距离课件4苏教版必修2(18张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.5平面上两点间的距离课件4苏教版必修2(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 180.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:31:36 | ||
图片预览



文档简介
课件18张PPT。
2.1.5 平面上两点间的距离 教学目标:
1、掌握平面上两点间的距离公式;
2、掌握平面上线段的中点坐标公式;
3、能运用两点间的距离公式和中点坐标公式解决一些简单问题;
重点:两点间的距离公式和中点坐标公式
难点:两点间的距离公式的推导及分类讨论思想的渗透
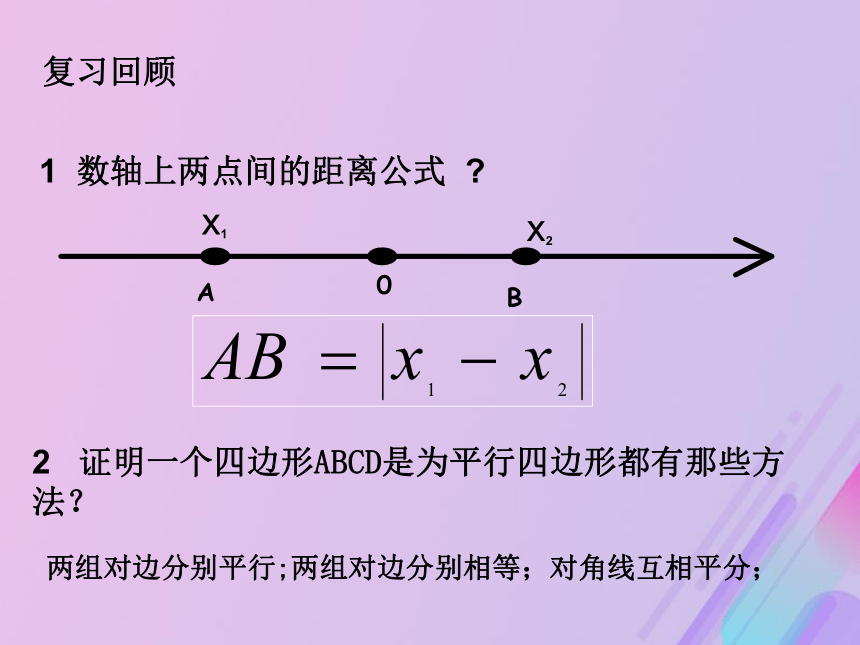
教法:引导、探究1 数轴上两点间的距离公式 ?x1x22 证明一个四边形ABCD是为平行四边形都有那些方法?两组对边分别平行;两组对边分别相等;对角线互相平分;复习回顾一、平面上两点间的距离1、已知点A(-1,3),B(3,-2),C(6,-1)
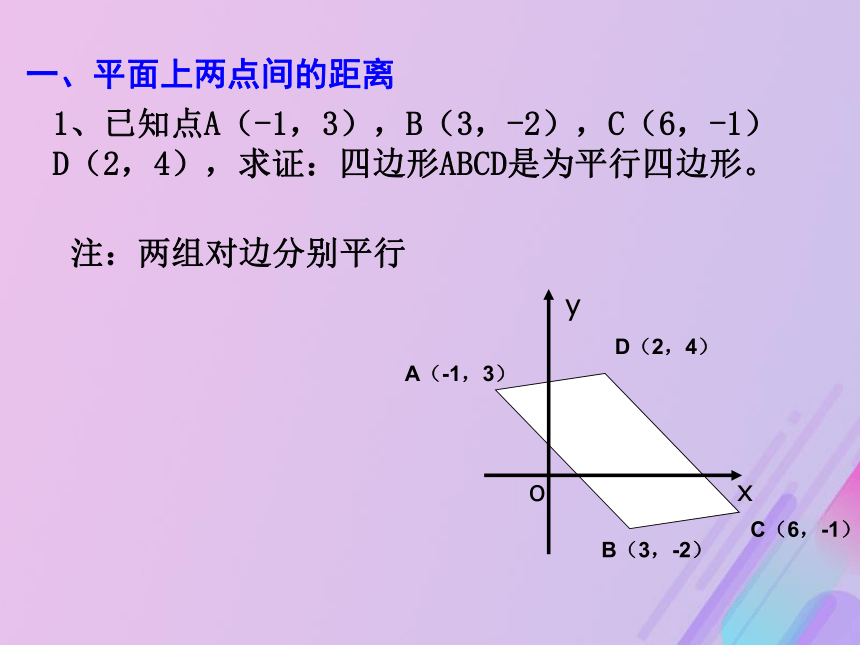
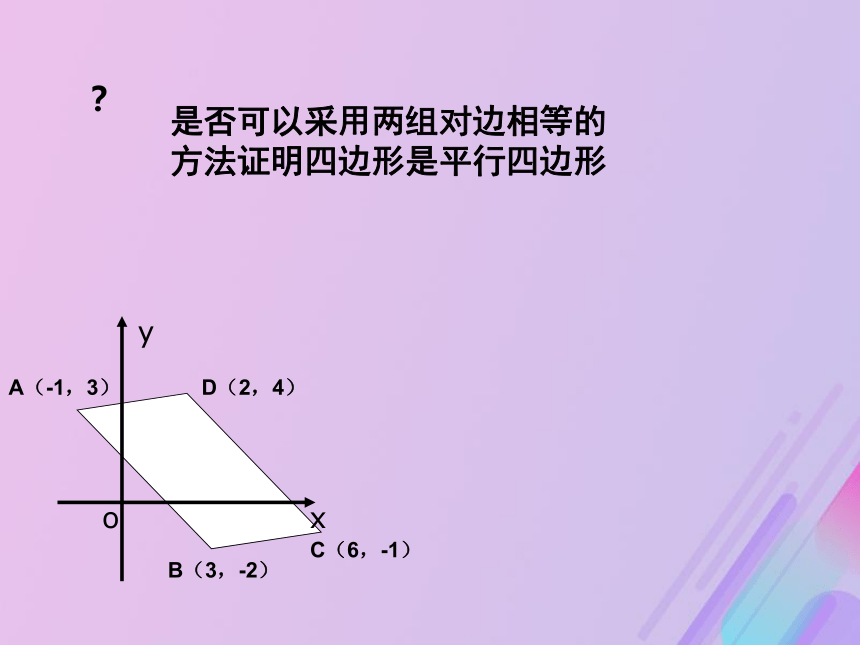
D(2,4),求证:四边形ABCD是为平行四边形。A(-1,3)B(3,-2)C(6,-1)D(2,4)注:两组对边分别平行是否可以采用两组对边相等的方法证明四边形是平行四边形A(-1,3)B(3,-2)C(6,-1)D(2,4)?P(-1,-2) 过A,B 分别向x轴,y轴作垂线,两条垂线相交于点P,则点P的坐标为 (-1,-2).于是
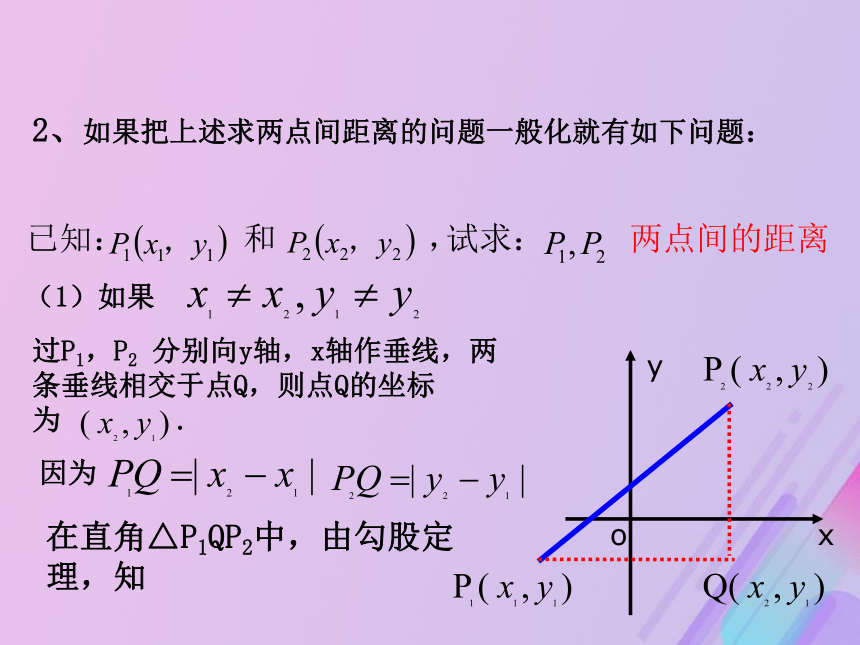
PA=|3-(-2)|=5, PB=|3-(-1)|=4在直角△APB中,由勾股定理,知类似可得CD= ,所以AB=CD,同理 BC=DA,所以四边形ABCD是平行四边形。过P1,P2 分别向y轴,x轴作垂线,两条垂线相交于点Q,则点Q的坐标为 .2、如果把上述求两点间距离的问题一般化就有如下问题:试求: 两点间的距离已知: 和 ,在直角△P1QP2中,由勾股定理,知因为(1)如果(3)如果 x1=x2(2)如果 y1=y21 平面上两点间的距离公式;练习1、求A、B两点间的距离
(1)A(-2,0),B(-2,-3);(2)A(0,-3),B(-3,-3)
(3)A(3,5),B(-3,3)
2、已知A(0,10),B(a,-5)两点间的距离是17,求实数a的值二、平面上两点的中点坐标 第三种方法:对角线互相平分的四边形是平行四边形,证明对角线AC和BD的中点相同,也可以说明四边形ABCD是平行四边形。 那么如何求对角线AC和BD中点的坐标呢?思考:是否可以用第三种证明平行四边形的方法来证明呢? 1、求AC中点的坐标 已知点A(-1,3),C(6,-1),求线段AC中点的坐标? A(-1,3)B(3,-2)C(6,-1)D(2,4)E(-1,-1)
设线段AC的中点M的坐标为(x,y),过A,C 分别做x轴y轴的垂线,交点为E坐标为(-1,-1)E(-1,-1)x为点E,C横坐标的平均数
y为点E,A横坐标的平均数 一般地,对于平面上的两点P1(x1,y1),
P2(x2,y2),线段P1P2的中点是M(x0,y0),则 :2 线段中点的坐标公式 在中点的坐标公式中 涉及三个点 P1(x1,y1), P2(x2,y2)及它们的中点M(x0,y0),只要知道其中两个点的坐标就可以求出另外一个点 , 中点的坐标公式的变形公式 练习 2、已知 的顶点坐标为A(3,2),B(1,0),
C(2,1) ,求AB边上的中线CM的长 1、求线段AB的中点坐标.
① A(8,10) , B(-4,4) ②3、已知两点P(1,-4),A(3,2),求点A关于点P的对称点B的坐标。4、已知点A(1,-2),分别求点A关于原点,x轴,y轴的对称点的坐标。课后思考题初中我们证明过这样一个问题:
直角三角形斜边的中线长等于斜边长的一半。 你能用解析几何的方法(坐标法)证明
此问题吗? 三、本节小结1、两点间的距离公式2 中点坐标公式及其变形公式
1、掌握平面上两点间的距离公式;
2、掌握平面上线段的中点坐标公式;
3、能运用两点间的距离公式和中点坐标公式解决一些简单问题;
重点:两点间的距离公式和中点坐标公式
难点:两点间的距离公式的推导及分类讨论思想的渗透
教法:引导、探究1 数轴上两点间的距离公式 ?x1x22 证明一个四边形ABCD是为平行四边形都有那些方法?两组对边分别平行;两组对边分别相等;对角线互相平分;复习回顾一、平面上两点间的距离1、已知点A(-1,3),B(3,-2),C(6,-1)
D(2,4),求证:四边形ABCD是为平行四边形。A(-1,3)B(3,-2)C(6,-1)D(2,4)注:两组对边分别平行是否可以采用两组对边相等的方法证明四边形是平行四边形A(-1,3)B(3,-2)C(6,-1)D(2,4)?P(-1,-2) 过A,B 分别向x轴,y轴作垂线,两条垂线相交于点P,则点P的坐标为 (-1,-2).于是
PA=|3-(-2)|=5, PB=|3-(-1)|=4在直角△APB中,由勾股定理,知类似可得CD= ,所以AB=CD,同理 BC=DA,所以四边形ABCD是平行四边形。过P1,P2 分别向y轴,x轴作垂线,两条垂线相交于点Q,则点Q的坐标为 .2、如果把上述求两点间距离的问题一般化就有如下问题:试求: 两点间的距离已知: 和 ,在直角△P1QP2中,由勾股定理,知因为(1)如果(3)如果 x1=x2(2)如果 y1=y21 平面上两点间的距离公式;练习1、求A、B两点间的距离
(1)A(-2,0),B(-2,-3);(2)A(0,-3),B(-3,-3)
(3)A(3,5),B(-3,3)
2、已知A(0,10),B(a,-5)两点间的距离是17,求实数a的值二、平面上两点的中点坐标 第三种方法:对角线互相平分的四边形是平行四边形,证明对角线AC和BD的中点相同,也可以说明四边形ABCD是平行四边形。 那么如何求对角线AC和BD中点的坐标呢?思考:是否可以用第三种证明平行四边形的方法来证明呢? 1、求AC中点的坐标 已知点A(-1,3),C(6,-1),求线段AC中点的坐标? A(-1,3)B(3,-2)C(6,-1)D(2,4)E(-1,-1)
设线段AC的中点M的坐标为(x,y),过A,C 分别做x轴y轴的垂线,交点为E坐标为(-1,-1)E(-1,-1)x为点E,C横坐标的平均数
y为点E,A横坐标的平均数 一般地,对于平面上的两点P1(x1,y1),
P2(x2,y2),线段P1P2的中点是M(x0,y0),则 :2 线段中点的坐标公式 在中点的坐标公式中 涉及三个点 P1(x1,y1), P2(x2,y2)及它们的中点M(x0,y0),只要知道其中两个点的坐标就可以求出另外一个点 , 中点的坐标公式的变形公式 练习 2、已知 的顶点坐标为A(3,2),B(1,0),
C(2,1) ,求AB边上的中线CM的长 1、求线段AB的中点坐标.
① A(8,10) , B(-4,4) ②3、已知两点P(1,-4),A(3,2),求点A关于点P的对称点B的坐标。4、已知点A(1,-2),分别求点A关于原点,x轴,y轴的对称点的坐标。课后思考题初中我们证明过这样一个问题:
直角三角形斜边的中线长等于斜边长的一半。 你能用解析几何的方法(坐标法)证明
此问题吗? 三、本节小结1、两点间的距离公式2 中点坐标公式及其变形公式
