2018年高中数学第1章立体几何初步1.1.2圆柱、圆锥、圆台和球课件3苏教版必修2(25张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.1.2圆柱、圆锥、圆台和球课件3苏教版必修2(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 341.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 09:36:52 | ||
图片预览






文档简介
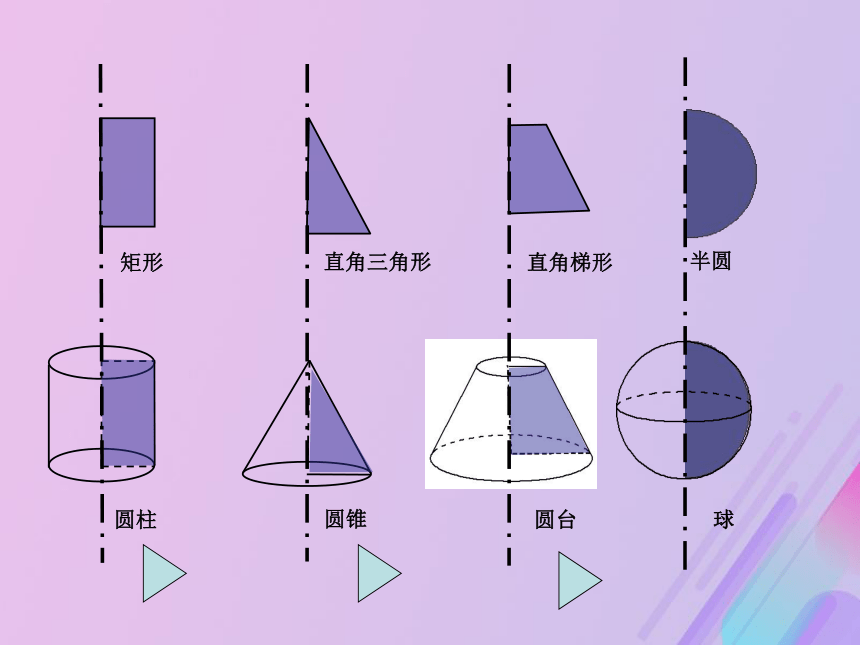
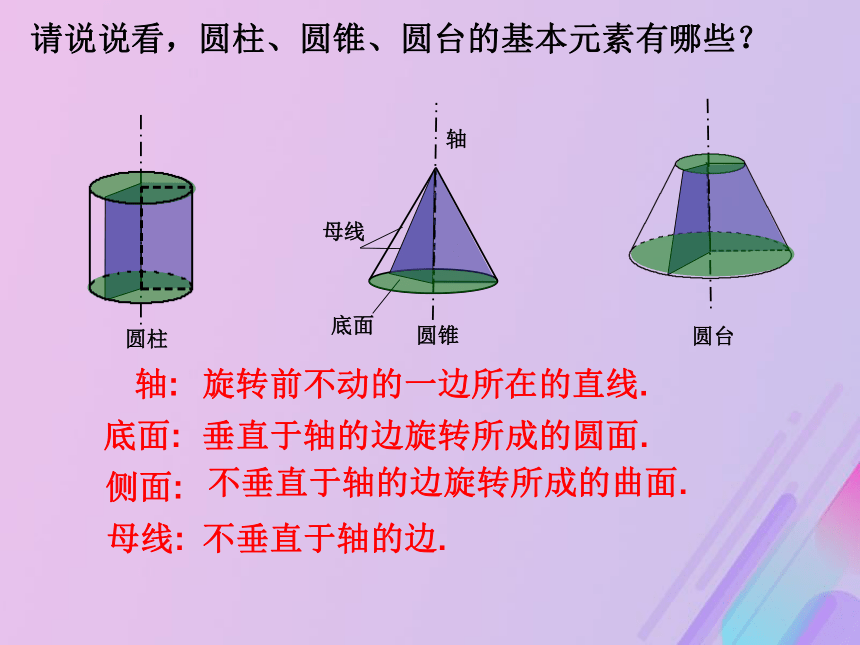
课件25张PPT。请思考:观察这些几何体,它们有什么共同特点或生成规律?圆柱、圆锥、圆台和球 分别以矩形、直角三角形的直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而成的曲面所围成的几何体, 分别叫做圆柱,圆锥,圆台。 半圆绕着它的直径所在的直线旋转一周所形成的曲面叫做球面,球面围成的几何体叫做球体,简称球。轴:侧面:垂直于轴的边旋转所成的圆面.不垂直于轴的边旋转所成的曲面.母线:不垂直于轴的边.旋转前不动的一边所在的直线.底面:请说说看,圆柱、圆锥、圆台的基本元素有哪些?球轴半圆的圆心叫做球的球心,
半圆的半径叫做球的半径,
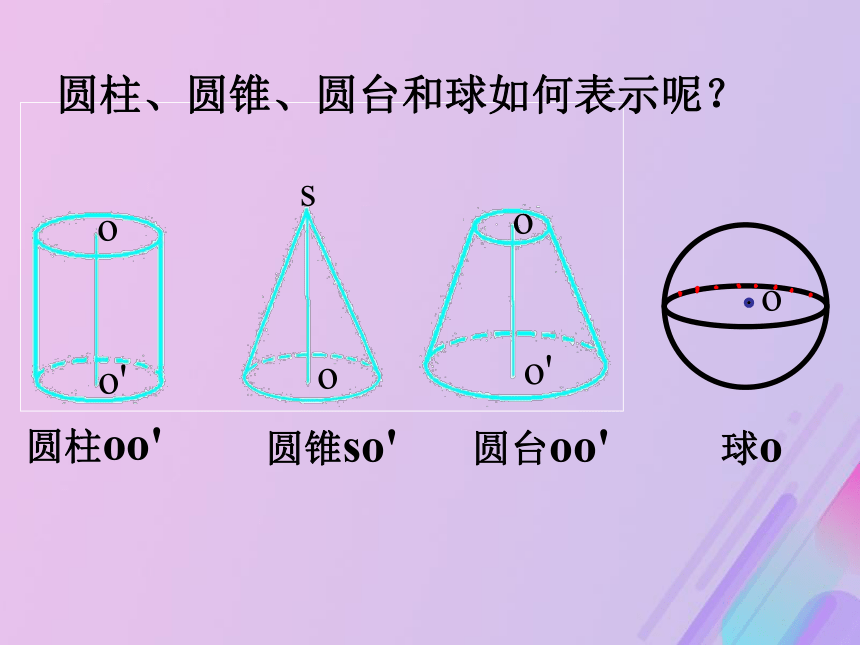
半圆的直径叫做球的直径。球的基本元素又有哪些呢?圆柱oo'圆柱、圆锥、圆台和球如何表示呢?圆锥so'圆台oo'球o1.平行于圆柱,圆锥,圆台的
底面的截面是什么图形?
2.过圆柱,圆锥,圆台的旋转
轴的截面是什么图形?性质1:平行于底面的截面都是圆。性质2:过轴的截面(轴截面)分别是全等的矩
形,等腰三角形,等腰梯形。用一个平面去截球体得到的截面是什么图形? 性质3:用一个平面去截球体得到的截面是一个圆。类比棱柱、棱锥、棱台的生成过程,认识圆柱、圆锥、
圆台的结构特征.类比圆的定义,请尝试从集合的角度定义球!OO圆:球:和一个定点距离等于定长的点的集合.和一个定点距离等于定长的点的集合.平面内空间中旋转面:旋转体:封闭的旋转面围成的几何体.一般地,一条平面曲线绕它所在的平面内的一条定直线旋转所成的曲面.问题1.如图,将直角梯形ABCD绕AB边所在的直线旋转一周,由此形成的几何体是由哪些简单几何体构成的?如图,将平行四边形ABCD绕AB边所在的直线旋转一周,
由此形成的几何体是由哪些简单几何体构成的?即时训练1矩形直角三角形圆直角梯形圆柱圆锥球圆台即时训练2问题2.指出图中的几何体是由哪些简单几何体构成的?割去四棱柱补上两个四棱柱指出图中的几何体是由哪些简单几何体构成的?即时训练3矫正反馈1.给出以下四个命题,其中正确的命题有(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
(2)圆锥的顶点与底面圆周上的任意一点的连线是圆锥的母线;
(3)经过圆台的任意两条母线可作一个截面;
(4)圆柱的任意两条母线互相平行;
(5)球面的截面一定是圆;
(6)过圆锥顶点的截面是等腰三角形;
(7)过圆台上、下底面中心的截面是等腰三角形。矫正反馈2.如图,在平面直角坐标系中有一个直角三角形ABC,现将该三角形分别绕x轴,y轴各旋转一周,得到两个几何体,指出它们各是什么几何体或各是由哪些几何体组合而成的。CxyAB4.圆台的上、下底面的直径分别为2cm,10cm, 高为3cm,则圆台母线长为_______. 矫正反馈3.用一张长为8cm,宽为6cm的矩形纸卷成一个母线长为6cm的圆柱,则圆柱轴截面的面积为_______. 谈谈你这节课的收获吧! 请同学们课后找一找生活中具有圆柱、圆锥、圆台和球几何结构特征的实物,小组之间相互说说它是怎样旋转形成的?它又是由哪些简单几何体构成的.谢谢大家!
半圆的半径叫做球的半径,
半圆的直径叫做球的直径。球的基本元素又有哪些呢?圆柱oo'圆柱、圆锥、圆台和球如何表示呢?圆锥so'圆台oo'球o1.平行于圆柱,圆锥,圆台的
底面的截面是什么图形?
2.过圆柱,圆锥,圆台的旋转
轴的截面是什么图形?性质1:平行于底面的截面都是圆。性质2:过轴的截面(轴截面)分别是全等的矩
形,等腰三角形,等腰梯形。用一个平面去截球体得到的截面是什么图形? 性质3:用一个平面去截球体得到的截面是一个圆。类比棱柱、棱锥、棱台的生成过程,认识圆柱、圆锥、
圆台的结构特征.类比圆的定义,请尝试从集合的角度定义球!OO圆:球:和一个定点距离等于定长的点的集合.和一个定点距离等于定长的点的集合.平面内空间中旋转面:旋转体:封闭的旋转面围成的几何体.一般地,一条平面曲线绕它所在的平面内的一条定直线旋转所成的曲面.问题1.如图,将直角梯形ABCD绕AB边所在的直线旋转一周,由此形成的几何体是由哪些简单几何体构成的?如图,将平行四边形ABCD绕AB边所在的直线旋转一周,
由此形成的几何体是由哪些简单几何体构成的?即时训练1矩形直角三角形圆直角梯形圆柱圆锥球圆台即时训练2问题2.指出图中的几何体是由哪些简单几何体构成的?割去四棱柱补上两个四棱柱指出图中的几何体是由哪些简单几何体构成的?即时训练3矫正反馈1.给出以下四个命题,其中正确的命题有(1)在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;
(2)圆锥的顶点与底面圆周上的任意一点的连线是圆锥的母线;
(3)经过圆台的任意两条母线可作一个截面;
(4)圆柱的任意两条母线互相平行;
(5)球面的截面一定是圆;
(6)过圆锥顶点的截面是等腰三角形;
(7)过圆台上、下底面中心的截面是等腰三角形。矫正反馈2.如图,在平面直角坐标系中有一个直角三角形ABC,现将该三角形分别绕x轴,y轴各旋转一周,得到两个几何体,指出它们各是什么几何体或各是由哪些几何体组合而成的。CxyAB4.圆台的上、下底面的直径分别为2cm,10cm, 高为3cm,则圆台母线长为_______. 矫正反馈3.用一张长为8cm,宽为6cm的矩形纸卷成一个母线长为6cm的圆柱,则圆柱轴截面的面积为_______. 谈谈你这节课的收获吧! 请同学们课后找一找生活中具有圆柱、圆锥、圆台和球几何结构特征的实物,小组之间相互说说它是怎样旋转形成的?它又是由哪些简单几何体构成的.谢谢大家!
