2019届北师大版(文科数学) 垂直关系的判定 单元测试
文档属性
| 名称 | 2019届北师大版(文科数学) 垂直关系的判定 单元测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 00:00:00 | ||
图片预览




文档简介
2019届北师大版(文科数学) 垂直关系的判定 单元测试
一、选择题
1.已知l⊥α,则过l与α垂直的平面( )
A. 有1个 B. 有2个
C. 有无数个 D. 不存在
【答案】C
【解析】
【分析】
由面面垂直的判定定理可得答案.
【详解】已知l⊥α,由面面垂直的判定定理可得过l与α垂直的平面有无数个.
故选C.
【点睛】本题考查面面垂直的判定定理的应用,属基础题.
2.若三条直线OA,OB,OC两两垂直,则直线OA垂直于( )
A. 平面OAB B. 平面OAC
C. 平面OBC D. 平面ABC
【答案】C
【解析】
【分析】
根据OA⊥OB,OA⊥OC,而OB∩OC=O,满足直线与平面垂直的判定定理,从而得到结论.
【详解】∵OA⊥OB,OA⊥OC,而OB∩OC=O
满足直线与平面垂直的判定定理
∴直线OA垂直于平面OBC
故选:C.
【点睛】本题主要考查了直线与平面垂直的判定,同时考查了化归与转化的数学思想方法,以及空间想象能力、推理论证能力.
3.空间中直线l和三角形的两边AC,BC同时垂直,则这条直线和三角形的第三边AB的位置关系是( )
A. 平行 B. 垂直
C. 相交 D. 不确定
【答案】B
【解析】
【分析】
根据直线与平面的判定定理可知,直线与平面内两相交直线垂直则垂直与这个平面,再根据线面垂直的性质可知,该直线垂直与平面内任意直线,从而得到结论.
【详解】由于直线l和三角形的两边AC,BC同时垂直,而这两边相交于点C,所以直线l和三角形所在的平面垂直,又因三角形的第三边AB在这个平面内,所以l⊥AB.
故选:B.
【点睛】本题主要考查了直线与平面垂直的判定,以及线面垂直的性质,同时考查了空间想象能力,属于基础题.
4.从空间一点P向二面角α-l-β的两个面α,β分别作垂线PE,PF,E,F为垂足,若∠EPF=60°,则二面角α-l-β的平面角的大小是( )
A. 60° B. 120°
C. 60°或120° D. 不确定
【答案】C
【解析】
【分析】
确定∠EPF=60°就是两个平面α和β的法向量的夹角,然后利用二面角的平面角和法向量的夹角直接的关系确定即可.
【详解】∠EPF=60°就是两个平面α和β的法向量的夹角,
它与二面角的平面角相等或互补,
故二面角的平面角的大小为60°或120°.
故选:C.
【点睛】本题重点考查了平面的法向量、法向量的夹角与平面所成的二面角之间的关系等知识,属于中档题.
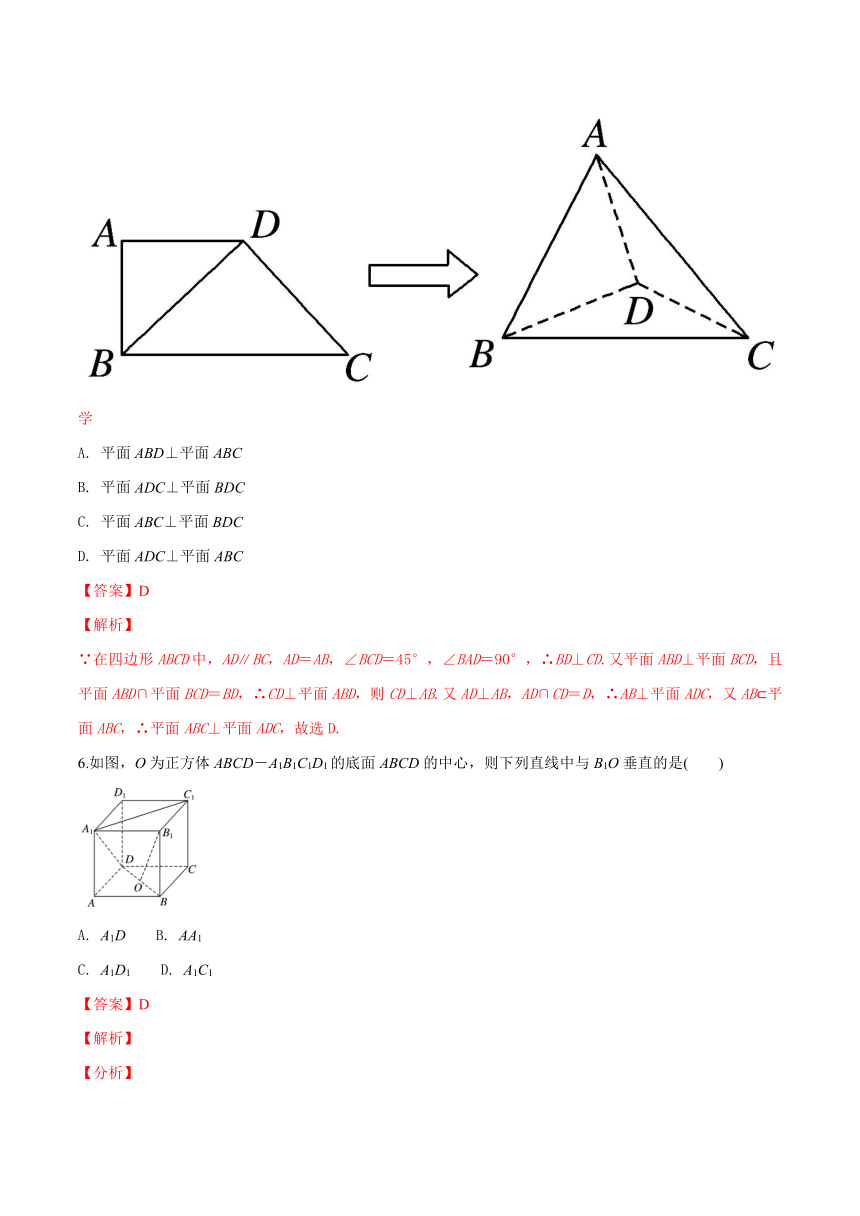
5.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成几何体A-BCD,则在几何体A-BCD中,下列结论正确的是( )
学
A. 平面ABD⊥平面ABC
B. 平面ADC⊥平面BDC
C. 平面ABC⊥平面BDC
D. 平面ADC⊥平面ABC
【答案】D
【解析】
∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,∴CD⊥平面ABD,则CD⊥AB.又AD⊥AB,AD∩CD=D,∴AB⊥平面ADC,又AB?平面ABC,∴平面ABC⊥平面ADC,故选D.
6.如图,O为正方体ABCD-A1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是( )
A. A1D B. AA1
C. A1D1 D. A1C1
【答案】D
【解析】
【分析】
连接B1D1,根据正方体的性质,得到BB1⊥平面A1B1C1D1,从而有BB1⊥A1C1.再根据A1B1C1D1是正方形,得到B1D1⊥A1C1,结合B1D1、BB1是平面BB1D1D内的相交直线,得到A1C1⊥平面BB1D1D,可得A1C1⊥B1O,因此可得正确答案.
【详解】连接B1D1,
∵ABCD-A1B1C1D1是正方体
∴BB1⊥平面A1B1C1D1
∵A1C1?平面A1B1C1D1,
∴BB1⊥A1C1
∵A1B1C1D1是正方形
∴B1D1⊥A1C1
∵B1D1、BB1是平面BB1D1D内的相交直线
∴A1C1⊥平面BB1D1D
∵B1O?平面BB1D1D
∴A1C1⊥B1O
故选:D.
【点睛】本题给出正方体内的一条直线,寻找与之垂直的直线,着重考查了空间中直线与直线之间的位置关系、线面垂直的判定与性质等知识点,属于基础题.
7.在正方体ABCD-A1B1C1D1中,截面A1BD与底面ABCD所成二面角A1-BD-A的正切值为( )
A. B. C. D.
【答案】C
【解析】
如图,在正方体A1B1C1D1-ABCD中,设AC、BD交于O,连A1O,
∵BD⊥AC,BD⊥AA1,AC∩AA1=A,
∴BD⊥平面AA1O,
∴BD⊥A1O,
∴∠A1OA为二面角的平面角.
在中,.
即截面A1BD与底面ABCD所成二面角A1-BD-A的正切值等于。选C。
点睛:
求二面角时要体现“一找二证三计算”的解题思路,其中作出二面角的平面角是解题的关键。作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
二、填空题
8.在三棱锥V-ABC中,当三条侧棱VA,VB,VC之间满足条件 时,有VC⊥AB.(注:填上你认为正确的条件即可)
【答案】VC⊥VA,VC⊥VB(答案不唯一,只要能保证VC⊥AB即可)
【解析】
【分析】
若VC⊥VA且VC⊥VB,则有VC⊥平面VAB,从而有VC⊥AB.
【详解】VC⊥VA且VC⊥VB
∴VC⊥平面VAB
∴VC⊥AB
故答案为:VC⊥VA且VC⊥VB(答案不唯一,只要能保证VC⊥AB即可)
【点睛】本题主要考查棱锥的结构特征,主要涉及了棱锥中的线线,线面关系,属基础题.
9.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是 .
【答案】
【解析】
【分析】
由P是等腰三角形ABC所在平面外一点,PA⊥平面ABC,我们易得PB=PC,取BC的中点D,则AD⊥BC,且PD⊥BC,利用勾股定理我们易求出AD的长,进而求出PD的长,即点P到BC的距离.
【详解】如下图所示:
设D为等腰三角形ABC底面上的中点,则PD长即为P点到BC的距离
又∵AD即为三角形的中线,也是三角形BC边上的高
∵BC=6,AB=AC=5,易得
在直角三角形PAD中,又∵PA=8
∴PD=.
故答案为.
【点睛】本题考查的知识点是空间点、线、面之间的距离,其中利用三角形的性质,做出PD即为点P到BC的垂线段是解答本题的关键.
10.已知α,β是两个不同的平面,m,n是平面α及β之外的两条不同直线,给出四个论断:
①m⊥n;②α⊥β;③n⊥β;④m⊥α.
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: .(用序号表示)
【答案】①③④?②(或②③④?①)
【解析】
【分析】
m⊥α,n⊥β,α⊥β,由面面垂直的性质定理得m⊥n;m⊥n,m⊥α,n⊥β,由面面垂直的判定定理得α⊥β.
【详解】m⊥α,n⊥β,α⊥β?m⊥n,由面面垂直的性质定理得m⊥n正确;
m⊥n,m⊥α,n⊥β?α⊥β,由面面垂直的判定定理得α⊥β正确;
α⊥β,n⊥β,m⊥n?m⊥α,这里m与α相交、平行或m?α,故m⊥α不正确;
m⊥n,α⊥β,m⊥α?n⊥β,这里n与β相交、平行或n?β,故n⊥β不正确.
故答案为:m⊥α,n⊥β,α⊥β?m⊥n或m⊥n,m⊥α,n⊥β?α⊥β.
即①③④?②(或②③④?①).
【点睛】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.
11.已知三棱锥D-ABC的三个侧面与底面全等,且AB=AC=,BC=2,则二面角D-BC-A的大小为 .
【答案】90°
【解析】
如图,由题意知AB=AC=BD=CD=,BC=AD=2.
取BC的中点E,连接DE、AE,则AE⊥BC,DE⊥BC,所以∠DEA为所求二面角的平面角.
易得AE=DE=,又AD=2,
所以∠DEA=90°.
三、解答题
12.如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2,E,F分别是AD,PC的中点.证明:PC⊥平面BEF.
【答案】证明见解析
【解析】
【分析】
如图,连接PE,EC,证明△PEC是等腰三角形.得到EF⊥PC.,进而证明BF⊥PC.,即可证明PC⊥平面BEF..
【详解】证明 如图,连接PE,EC,
在Rt△PAE和Rt△CDE中,PA=AB=CD,AE=DE,
∴PE=CE,
即△PEC是等腰三角形.
又F是PC的中点,
∴EF⊥PC.
又BP==2=BC,F是PC的中点,
∴BF⊥PC.
又BF∩EF=F,
∴PC⊥平面BEF.
【点睛】本题考查直线与平面垂直的证明,属基础题.
13.如图所示,在正三棱柱ABC-A1B1C1中,E为BB1的中点,求证:截面A1CE⊥侧面ACC1A1.
【答案】证明见解析
【解析】
【分析】
如图所示,取A1C的中点F,AC的中点G,连接FG,EF,BG,可证明EF⊥A1C.,进而证明四边形BEFG是矩形,可得EF⊥FG.,由此可证EF⊥侧面ACC1A1.,继而得到
截面A1CE⊥侧面ACC1A1.
【详解】证明 如图所示,取A1C的中点F,AC的中点G,连接FG,EF,BG,则FG∥AA1,且GF=AA1.
因为BE=EB1,A1B1=CB,∠A1B1E=∠CBE=90°,所以△A1B1E≌△CBE,
所以A1E=CE.
因为F为A1C的中点,所以EF⊥A1C.
又FG∥AA1∥BE,GF=AA1=BE,且BE⊥BG,所以四边形BEFG是矩形,
所以EF⊥FG.
因为A1C∩FG=F,所以EF⊥侧面ACC1A1.
又因为EF?平面A1CE,所以截面A1CE⊥侧面ACC1A1
【点睛】本题考查空间线面关系,正三棱柱的性质,逻辑思维能力,空间想象能力及运算能力.
四、探究与拓展
14.在正四面体P?ABC中,D,E,F分别是AB,BC,CA的中点,则下面四个结论中不成立的是( )
A. BC∥平面PDF
B. DF⊥平面PAE
C. 平面PDF⊥平面ABC
D. 平面PAE⊥平面ABC
【答案】C
【解析】
【分析】
根据直线与平面平行、垂直的判定及两平面垂直的判定,可逐项判定.
【详解】可画出对应图形,如图所示,则BC∥DF.又DF?平面PDF,BC?平面PDF,
所以BC∥平面PDF,故A成立.
由AE⊥BC,PE⊥BC,BC∥DF,知DF⊥AE,DF⊥PE,所以DF⊥平面PAE,故B成立.
又DF?平面ABC,所以平面ABC⊥平面PAE,故D成立.
【点睛】本题主要考查了线面垂直的判定定理及面面垂直的判定,属于中档题.
15.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)求AE等于何值时,二面角D1-EC-D的大小为45°?
【答案】(1)证明见解析
(2) EB=,AE=2-.
【解析】
【分析】
(1) 连接D1A,D1B.易证A1D⊥AD1.又由题意知AB⊥A1D,且AB∩AD1=A,
可得A1D⊥平面ABD1.即可证明 A1D⊥D1E.;
(2)过D作DF⊥EC于点F,连接D1F.,可证
【详解】(1)证明: 连接D1A,D1B.
∵在长方形A1ADD1中,AD=AA1=1,∴四边形A1ADD1为正方形,
∴A1D⊥AD1.又由题意知AB⊥A1D,且AB∩AD1=A,
∴A1D⊥平面ABD1.∵D1E平面ABD1,∠DFD1为二面角D1-EC-D的平面角,求其大小即可.
∴A1D⊥D1E.
(2)过D作DF⊥EC于点F,连接D1F.
∵D1D⊥平面DB,EC平面DB,∴D1D⊥EC.
又DF∩D1D=D,∴EC⊥平面D1DF.
∵D1F平面D1DF,∴EC⊥D1F,∴∠DFD1为二面角D1-EC-D的平面角,
∴∠DFD1=45°,又∠D1DF=90°,D1D=1,∴DF=1.
在Rt△DFC中,∵DC=2,∴∠DCF=30°,∴∠ECB=60°.
在Rt△EBC中,∵BC=1,∴EB=,AE=2-.
【点睛】本题考查利用线面垂直证明线线垂直,以及根据二面角的大小球其所要满足的体积,属中档题.
