2019届北师大版(文科数学) 简单几何体的侧面积 单元测试
文档属性
| 名称 | 2019届北师大版(文科数学) 简单几何体的侧面积 单元测试 |

|
|
| 格式 | zip | ||
| 文件大小 | 603.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-23 00:00:00 | ||
图片预览




文档简介
2019届北师大版(文科数学) 简单几何体的侧面积 单元测试
一、选择题
1.已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比是( )
A. B.
C. D.
【答案】A
【解析】
【分析】
根据圆柱的侧面展开图是一个正方形,得到圆柱的高和底面半径之间的关系,然后求出圆柱的表面积和侧面积即可得到结论.
【详解】设圆柱的底面半径为r,圆柱的高为h,
∵圆柱的侧面展开图是一个正方形,
∴2πr=h,即 .
∴圆柱的侧面积为2πrh=4π2r2,
圆柱的两个底面积为2πr2,∴圆柱的表面积为2πr2+2πrh=2πr2+4π2r2,
∴圆柱的表面积与侧面积的比为: ,
故选:A.
【点睛】本题主要考查圆柱的侧面积和表面积公式的计算,利用圆柱的侧面展开图是一个正方形,得到高和半径之间的关系是解决本题的关键.
2.将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积是( )
A. 4π B. 3π C. 2π D. π
【答案】C
【解析】
【分析】
边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,从而可求圆柱的侧面积.
【详解】边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,
则所得几何体的侧面积为:1×2π×1=2π,
故选:C.
【点睛】本题考查旋转体的侧面积的求法,考查计算能力.是基础题.
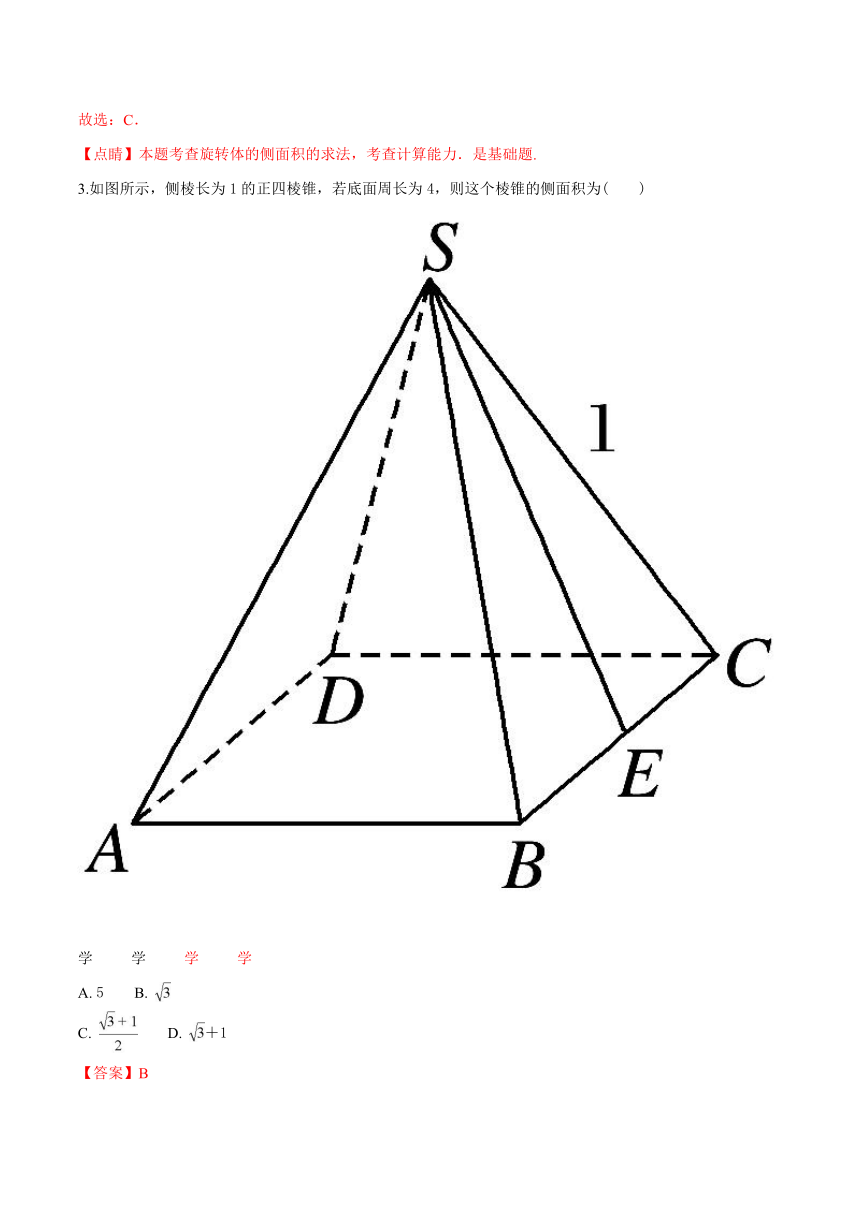
3.如图所示,侧棱长为1的正四棱锥,若底面周长为4,则这个棱锥的侧面积为( )
学 学 学 学
A. 5 B.
C. D. +1
【答案】B
【解析】
【分析】
由正四棱锥的侧棱长为1,底面周长为4,知这个棱锥侧面积是四个边长为1的等边三角形的面积之和.
【详解】:∵正四棱锥的侧棱长为1,底面周长为4,
∴这个棱锥侧面积是四个边长为1的等边三角形的面积之和,
∴这个棱锥侧面积 .
故选B.
【点睛】本题考查棱锥的侧面积的求法,解题时要认真审题,仔细解答,注意熟练掌握棱锥的结构特征.
4.圆台的一个底面圆周长是另一个底面圆周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面圆的半径为( )
A. 7 B. 6
C. 5 D. 3
【答案】A
【解析】
分析:设出上底面半径为r,利用圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,求出上底面半径,即可.
详解:设上底面半径为r,因为圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,所以S侧面积=π(r+3r)l=84π,r=7
故选:A.
点睛:本题是基础题,考查 圆台的侧面积公式,考查计算能力,牢记圆台的侧面积公示,直接代入公式即可.
5.某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为( )
A. B. π+ C. D.
【答案】C
【解析】
【分析】
三视图复原可知几何体是圆锥的一半,根据三视图数据,求出几何体的表面积.
【详解】由题目所给三视图可得,该几何体为圆锥的一半,那么该几何体的表面积为该圆锥表面积的一半与轴截面面积的和.
又该半圆锥的侧面展开图为扇形,所以侧面积为 ,底面积为
观察三视图可知,轴截面为边长为2的正三角形,所以轴截面面积为,
则该几何体的表面积为:.
故选C.
【点睛】本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.
6.在正方体ABCD?A1B1C1D1中,三棱锥D1?AB1C的表面积与正方体的表面积的比为( )
A. 1∶1 B. 1∶
C. 1∶ D. 1∶2
【答案】C
【解析】
【分析】
设出正方体ABCD-A1B1C1D1的棱长,求出正方体的表面积和三棱锥D1-AB1C的表面积即可.
【详解】设正方体ABCD-A1B1C1D1的棱长为a,则正方体ABCD-A1B1C1D1的表面积为S2=6a2,且三棱锥D1-AB1C为各棱长均为 的正四面体,
其中一个面的面积为 所以三棱锥D1-AB1C的表面积为: 所以三棱锥D1-AB1C的体积与正方体ABCD-A1B1C1D1的表面积之比为:
故选:C.
【点睛】本题考查了正方体与三棱锥的表面积公式的应用问题,是基础题目.
7.若一个圆锥的侧面展开图是面积为的半圆面,则该圆锥的母线与轴所成的角为( ).
A. B. C. D.
【答案】A
【解析】
设圆锥的母线长为,底面半径为,
∵圆锥的侧面展开图是面积为的半圆面,
∴,即,,又圆锥的侧面积公式,
∴,解得,即,,则,
∴,即圆锥的母线与圆锥的轴所成角的大小为,故选A.
8.某几何体的三视图如图所示(单位:cm),则该几何体的表面积等于( )
A. 8π cm2 B. 7π cm2
C. (5+)π cm2 D. 6π cm2
【答案】B
【解析】
【分析】
由三视图得此几何体是简单的组合体:上面是一个圆锥、下面是一个圆柱,并由三视图求出相应的数据,由表面积公式求出答案.
【详解】由三视图得,此几何体是简单的组合体,
上面是一个圆锥:底面是以1cm为半径、2cm为母线长的圆锥,
下面是底面是以1cm为半径、2cm为母线长的圆柱,
所以此几何体的表面积S=π×1×2+2π×1×2+π×12=7π(cm2),
故选:B.
【点睛】本题考查由三视图求几何体的表面积,解题关键是判断几何体的形状及几何量所对应的数据,考查空间想象能力.
二、填空题
9.已知圆锥的母线长为2,高为,则该圆锥的侧面积是 .
【答案】
【解析】
【分析】
求出圆锥的底面半径,求出底面周长,然后求出圆锥的侧面积.
【详解】已知圆锥的母线长为2,高为,则该圆锥的底面半径为:1
圆锥的底面周长为:2π,
所以圆锥的侧面积为:
故答案为:2π
【点睛】本题考查圆锥的侧面积,考查计算能力,圆锥的高,底面半径,母线构成勾股定理,是解决圆锥问题的常用方法,是基础题.
10.正四棱台的上、下两底面边长分别是方程x2-9x+18=0的两根,其侧面积等于两底面面积之和,则其侧面梯形的高为 .
【答案】
【解析】
【分析】
】解方程得出棱台的上下底面边长,根据面积关系和比例关系求出棱台的高和小棱锥的高.
【详解】解方程x2-9x+18=0得x=3或x=6,
∴棱台的上下底面边长分别为3,6.
设棱台的斜高为h
则 ,
∴h=.
即答案为.
【点睛】本题考查了棱台的结构特征,画出草图帮助观察各线段的关系比较重要.
11.如图所示,在棱长为4的正方体上底面中心位置打一个直径为2、深为4的圆柱形孔,则打孔后的几何体的表面积为 .
【答案】
【解析】
【分析】
打孔后的几何体的表面积是棱长为4的正方体的表面积减去两个半径为1的圆的面积.再加上圆柱的侧面积,
【详解】打孔后的几何体的表面积是棱长为4的正方体的表面积减去两个半径为1的圆的面积.再加上圆柱的侧面积
即答案为.
【点睛】本题考查几何体的表面积的求法,是中档题.
12.一个几何体的三视图如图所示,则该几何体的表面积为 .
【答案】38
【解析】
【分析】
由几何体的三视图可知,该几何体是长方体中间挖去一个圆柱体,根据数据计算表面积即可.
【详解】由几何体的三视图可知,该几何体是一组合体由几何体的三视图可知,该几何体是长方体中间挖去一个圆柱体.表面积应为长方体表面积减去圆柱底面积,再加上圆柱侧面积.
长方体长宽高分别为4,3,1,其表面积为(4×3+4×1+3×1)×2=38
圆柱底面半径为1,高为1
圆柱底面积为2×π×12=2π,侧面积为2π×1×1=2π
所以所求的表面积为38-2π+2π=38
及答案为38.
【点睛】本题考查由三视图求几何体的表面积,考查由三视图还原几何体直观图,考查柱体的表面积公式,本题是一个基础题.
三、解答题
13.如图所示是某几何体的三视图,它的主视图和左视图均为矩形,俯视图为正三角形.(长度单位:cm)
(1)该几何体是什么图形?
(2)画出该几何体的直观图(坐标轴如图所示),并求它的表面积.(只需作出图形,不要求写作法)
【答案】(1)三棱柱;(2)
【解析】
【分析】
(1)由三视图我们易判断,该几何体是一个三棱柱;
(2)根据直二侧画法,我们易得到其直观图.由已知三视图中标识的数据,我们易判断底面边长为4的正三角形,高为5,代入柱体的表面积公式,即可求出答案.
【详解】(1)由三视图可知该几何体是三棱柱.
(2)直观图如图所示.
因为该几何体的底面是边长为4 cm的等边三角形,高为2 cm,
所以它的表面积S三棱柱=2S底+S侧=2××42+3×4×2=(24+8)(cm2).
【点睛】本题考查的知识点是由三视图求面积,其中根据已知条件判断几何体的形状是解答的关键.
四、探究与拓展
14.如图所示,在一个空间几何体的三视图中,主视图和左视图都是直角三角形,其直角边长均为1,则该几何体的表面积为( )
A. 1+ B. 2+2 C. D. 2+
【答案】D
【解析】
【分析】
由已知中的三视图,分析出几何体的形状,进而判断出各个面的形状及边长,代入三角形和正方形面积公式,求出各个面的面积,可得几何体的表面积.
【详解】由已知中的三视图可得该几何体是一个四棱锥
底面是一个边长为1的正方形,故底面积S底=1
侧面有两个直角边长为1的等腰直角三角形,和两个边长分为 的直角三角形组成,故 ,
∴该几何体的表面积 .
故选:D.
【点睛】本题考查的知识点是由三视图求表面积,其中根据已知分析出几何体的形状及各面的边长是解答的关键.
15.如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.
(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
【答案】(1)h=3-3x(2)当 时,它的侧面积最大为π
【解析】
【分析】
(1)利用圆锥轴截面的特征可得圆柱的高h可表示为h=3-3x.
(2)由题意可得S圆柱侧=6π(x-x2),利用二次函数的性质可得当圆柱的底面半径为时,它的侧面积最大为π.
【详解】(1)设所求的圆柱的底面半径为x,它的轴截面如图,
BO=1,PO=3,圆柱的高为h,
由图,得=,即h=3-3x.
(2)∵S圆柱侧=2πhx=2π(3-3x)x=6π(x-x2),
当x=时,圆柱的侧面积取得最大值为π.
∴当圆柱的底面半径为时,它的侧面积最大为π.
【点睛】本题主要考查圆锥的空间结构特征,二次函数的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.
