2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程(20张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第二章圆锥曲线与方程2.3.1抛物线级其标准方程(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 614.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 10:46:53 | ||
图片预览







文档简介
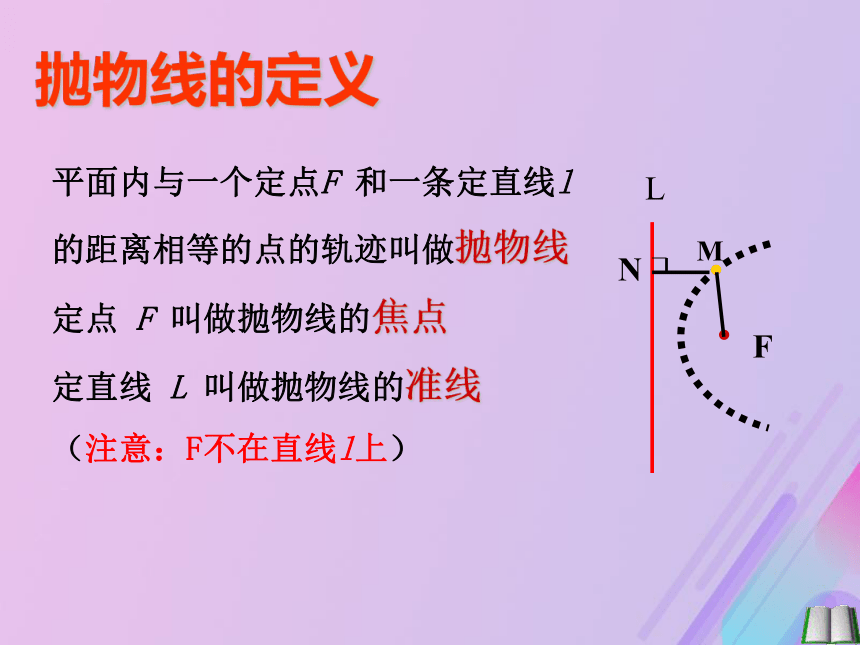
课件20张PPT。2.3.1抛物线及其标准方程 二次函数是开口向上或向下的抛物线。 对抛物线你有哪些认识?初中接触过类似的曲线吗? 平面内与一个定点F 和一条定直线l
的距离相等的点的轨迹叫做抛物线
定点 F 叫做抛物线的焦点
定直线 L 叫做抛物线的准线
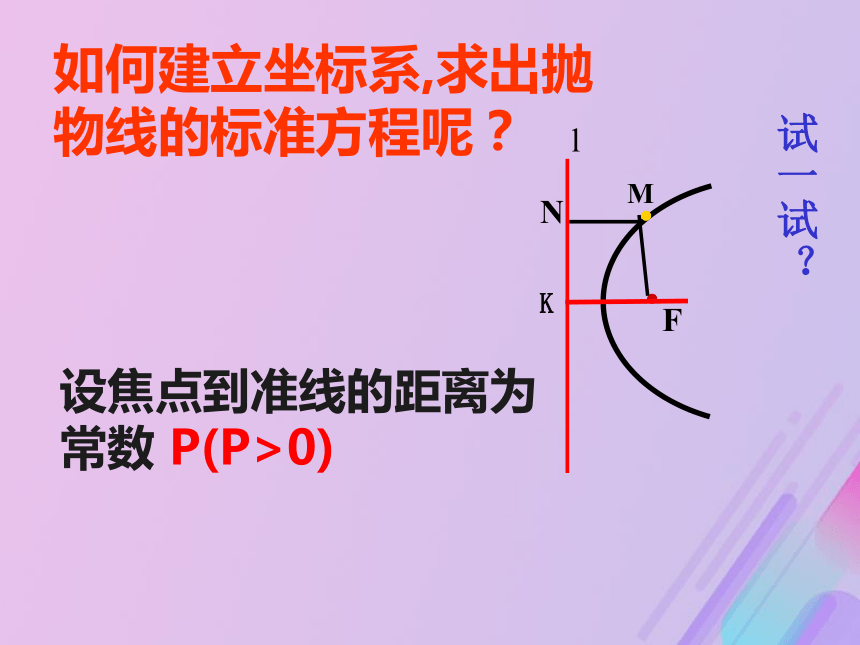
(注意:F不在直线l上)抛物线的定义回顾求曲线方程的一般步骤是:1、建立直角坐标系,设动点为(x,y)2、写出适合条件的x , y的关系式3、列方程4、化简5、(证明)设焦点到准线的距离为常数 P(P>0)试一试?K如何建立坐标系,求出抛物线的标准方程呢?坐标系的不同建立方法K设︱KF︱= p设动点M的坐标为(x,y) 由抛物线的定义可知,解:如图,取过焦点F且垂直于准线L的直线为x轴,线段KF的中垂线为y轴
抛物线标准方程的推导( p> 0) 方程 y2 = 2px(p>0)叫做
抛物线的标准方程其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离抛物线的标准方程但是,对于一条抛物线,它在坐标平面内的位置可以不同,所以建立的坐标系也不同,所得抛物线的方程也不同,所以抛物线的标准方程还有其它形式。
方程 y2 = 2px(p>0)表示的抛物线,其焦点位于X轴的正半轴上,其准线交于X轴的负半轴抛物线的标准方程抛物线的标准方程抛物线的标准方程还有哪些形式?其它形式的抛物线的焦点与准线又如何表示呢?向右
向左
向上
向下
根据上表中抛物线的标准方程的不同 形式与图形、焦点坐标、准线方程对应关系,如何判断抛物线的焦点位置,开口方向?想一想:第一:一次项的变量为抛物线的对 称轴,焦点就在对称轴上;
第二:一次项系数的正负决定了抛 物线的开口方向. 例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2课堂练习注意:求抛物线的焦点一定要先把抛物线化为标准形式例2:根据下列条件,写出抛物线的标准方程:(1)焦点是F(-2,0)(2)准线方程 是x = (3)焦点到准线的距离是2解:y2 =-8x解:y2 =x解:y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y1.由于抛物线的标准方程有四种形式,且每一种形式中 都只含一个系数p,因此只要给出确定p的一个条件,
就可以求出抛物线的标准方程 2.当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解.由例1.和例2.反思研究先定位,后定量
例3:求过点A(-3,2)的抛物线的标准方程。(1)焦点在y轴上,设抛物线的标准方程为 x2 =2py(p>0),
把A(-3,2)代入方程,解得p= (2)焦点在x轴上,设抛物线的标准方程为y2 = -2px(p>0) ,
把A(-3,2)代入方程,解得p=
∴抛物线的标准方程为x2 = y或y2 = x
解:由已经知,抛物线有二种情况: 例4.一种卫星接收天线的轴截面如右图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的口径(直径)为4.8m,深度为0.5m,试建立适当的坐标系,求抛物线的标准方程和焦点坐标。3.抛物线的标准方程类型与图象特征的
对应关系及判断方法2.抛物线的标准方程与其焦点、准线4.注重数形结合的思想 1.抛物线的定义课堂小结5.注重分类讨论的思想向右
1、课本作业;
2、你能发现二次函数与抛物线标准方程之间的关系吗?试写出你发现的结论;
3、已知抛物线方程为x=ay2(a≠0) 试讨论抛物线的开口方向、焦点坐标和准线方程。作业
的距离相等的点的轨迹叫做抛物线
定点 F 叫做抛物线的焦点
定直线 L 叫做抛物线的准线
(注意:F不在直线l上)抛物线的定义回顾求曲线方程的一般步骤是:1、建立直角坐标系,设动点为(x,y)2、写出适合条件的x , y的关系式3、列方程4、化简5、(证明)设焦点到准线的距离为常数 P(P>0)试一试?K如何建立坐标系,求出抛物线的标准方程呢?坐标系的不同建立方法K设︱KF︱= p设动点M的坐标为(x,y) 由抛物线的定义可知,解:如图,取过焦点F且垂直于准线L的直线为x轴,线段KF的中垂线为y轴
抛物线标准方程的推导( p> 0) 方程 y2 = 2px(p>0)叫做
抛物线的标准方程其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离抛物线的标准方程但是,对于一条抛物线,它在坐标平面内的位置可以不同,所以建立的坐标系也不同,所得抛物线的方程也不同,所以抛物线的标准方程还有其它形式。
方程 y2 = 2px(p>0)表示的抛物线,其焦点位于X轴的正半轴上,其准线交于X轴的负半轴抛物线的标准方程抛物线的标准方程抛物线的标准方程还有哪些形式?其它形式的抛物线的焦点与准线又如何表示呢?向右
向左
向上
向下
根据上表中抛物线的标准方程的不同 形式与图形、焦点坐标、准线方程对应关系,如何判断抛物线的焦点位置,开口方向?想一想:第一:一次项的变量为抛物线的对 称轴,焦点就在对称轴上;
第二:一次项系数的正负决定了抛 物线的开口方向. 例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2课堂练习注意:求抛物线的焦点一定要先把抛物线化为标准形式例2:根据下列条件,写出抛物线的标准方程:(1)焦点是F(-2,0)(2)准线方程 是x = (3)焦点到准线的距离是2解:y2 =-8x解:y2 =x解:y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y1.由于抛物线的标准方程有四种形式,且每一种形式中 都只含一个系数p,因此只要给出确定p的一个条件,
就可以求出抛物线的标准方程 2.当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解.由例1.和例2.反思研究先定位,后定量
例3:求过点A(-3,2)的抛物线的标准方程。(1)焦点在y轴上,设抛物线的标准方程为 x2 =2py(p>0),
把A(-3,2)代入方程,解得p= (2)焦点在x轴上,设抛物线的标准方程为y2 = -2px(p>0) ,
把A(-3,2)代入方程,解得p=
∴抛物线的标准方程为x2 = y或y2 = x
解:由已经知,抛物线有二种情况: 例4.一种卫星接收天线的轴截面如右图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线,经反射聚集到焦点处。已知接收天线的口径(直径)为4.8m,深度为0.5m,试建立适当的坐标系,求抛物线的标准方程和焦点坐标。3.抛物线的标准方程类型与图象特征的
对应关系及判断方法2.抛物线的标准方程与其焦点、准线4.注重数形结合的思想 1.抛物线的定义课堂小结5.注重分类讨论的思想向右
1、课本作业;
2、你能发现二次函数与抛物线标准方程之间的关系吗?试写出你发现的结论;
3、已知抛物线方程为x=ay2(a≠0) 试讨论抛物线的开口方向、焦点坐标和准线方程。作业
