2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(17张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 10:47:27 | ||
图片预览





文档简介
课件17张PPT。3.3.2利用导数研究函数的极值学习目标:数与形1.理解极值的定义。
2.掌握利用导数求函数极值的步骤,
能熟练地求函数的极值。
3.明确导数为零的点与极值点的逻辑关系。温故而知新:
一般地,设函数y=f(x)在某个区间(a,b)内有导数,
如果在这个区间内f′(x)>0,
那么函数y=f(x)在(a,b)为 ______ 函数;
如果在这个区间内f′(x)<0,
那么函数y=f(x)在(a,b)为 ______ 函数. 增减 问题一:
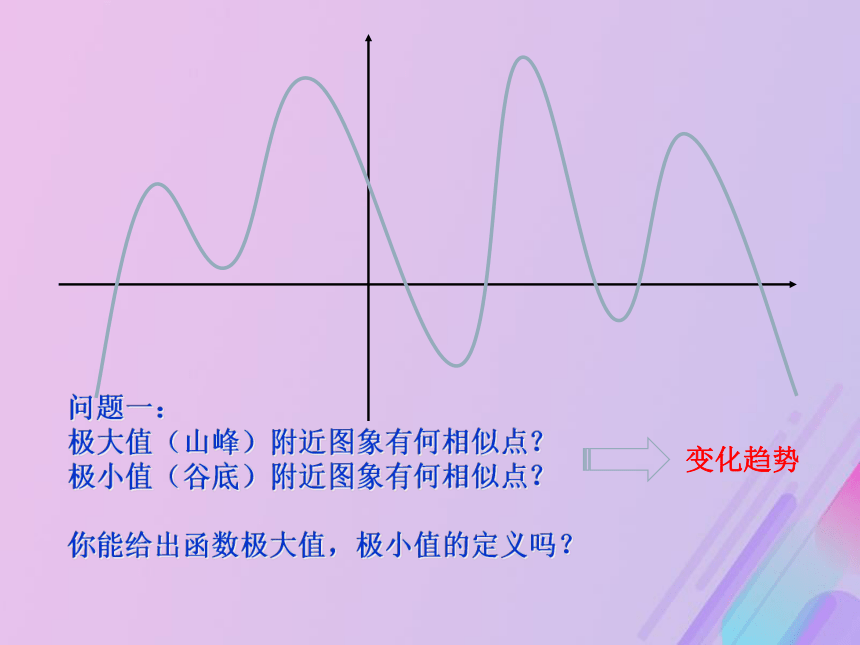
极大值(山峰)附近图象有何相似点?
极小值(谷底)附近图象有何相似点?
你能给出函数极大值,极小值的定义吗?变化趋势一、极值(极值点)的定义:一般地,设函数 在点 及附近有定义,
如果对 附近的所有点,都有 ,
就称 是函数的一个极大值,记作 ,
称 为函数的 。
如果对 附近的所有点,都有 ,
就称 是函数的一个极小值,记作 ,
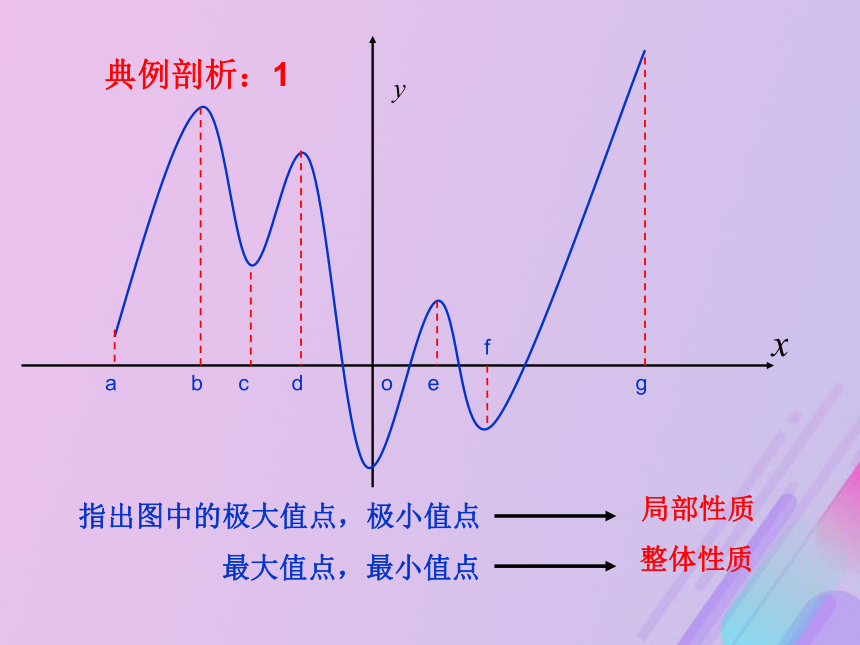
称 为函数的 。 极大值点极小值点abcdoefg指出图中的极大值点,极小值点
最大值点,最小值点局部性质整体性质典例剖析:1问题二:你能总结出利用导数求解函数极值的方法吗?
注:如果f′(x)在这个根的左右两侧符号不变,则f(x)在这个根处没有极值.
(即单调函数没有极值)
典例剖析: 问题三:对于可导函数 ,
是 在 处取极值的( )条件必要不充分典例剖析: 探究: (1)求函数的极值,并画出函数的草图;
(2)若方程 有3个解,求实数 的取值范围.
(3)讨论 方程解的个数.课堂小结:极值的概念
利用导数求解函数极值的步骤
导数为零的点与极值点的逻辑关系分类讨论知识部分: 方法部分:数形结合 函数与方程峰谷相连不分,今日顺境之错换得他日逆境,
今日逆境之智换得他日顺境;
两峰之间必有低谷,
经营低谷的方式决定着你攀登另一座高峰的速度
2.掌握利用导数求函数极值的步骤,
能熟练地求函数的极值。
3.明确导数为零的点与极值点的逻辑关系。温故而知新:
一般地,设函数y=f(x)在某个区间(a,b)内有导数,
如果在这个区间内f′(x)>0,
那么函数y=f(x)在(a,b)为 ______ 函数;
如果在这个区间内f′(x)<0,
那么函数y=f(x)在(a,b)为 ______ 函数. 增减 问题一:
极大值(山峰)附近图象有何相似点?
极小值(谷底)附近图象有何相似点?
你能给出函数极大值,极小值的定义吗?变化趋势一、极值(极值点)的定义:一般地,设函数 在点 及附近有定义,
如果对 附近的所有点,都有 ,
就称 是函数的一个极大值,记作 ,
称 为函数的 。
如果对 附近的所有点,都有 ,
就称 是函数的一个极小值,记作 ,
称 为函数的 。 极大值点极小值点abcdoefg指出图中的极大值点,极小值点
最大值点,最小值点局部性质整体性质典例剖析:1问题二:你能总结出利用导数求解函数极值的方法吗?
注:如果f′(x)在这个根的左右两侧符号不变,则f(x)在这个根处没有极值.
(即单调函数没有极值)
典例剖析: 问题三:对于可导函数 ,
是 在 处取极值的( )条件必要不充分典例剖析: 探究: (1)求函数的极值,并画出函数的草图;
(2)若方程 有3个解,求实数 的取值范围.
(3)讨论 方程解的个数.课堂小结:极值的概念
利用导数求解函数极值的步骤
导数为零的点与极值点的逻辑关系分类讨论知识部分: 方法部分:数形结合 函数与方程峰谷相连不分,今日顺境之错换得他日逆境,
今日逆境之智换得他日顺境;
两峰之间必有低谷,
经营低谷的方式决定着你攀登另一座高峰的速度
