2018年高中数学第1章立体几何初步1.1.1棱柱、棱锥和棱台课件4苏教版必修2(27张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.1.1棱柱、棱锥和棱台课件4苏教版必修2(27张) |  | |
| 格式 | zip | ||
| 文件大小 | 574.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 10:48:35 | ||
图片预览




文档简介
课件27张PPT。棱柱、棱锥和棱台从航空测绘到土木建筑以至家居装潢,——空间图形与
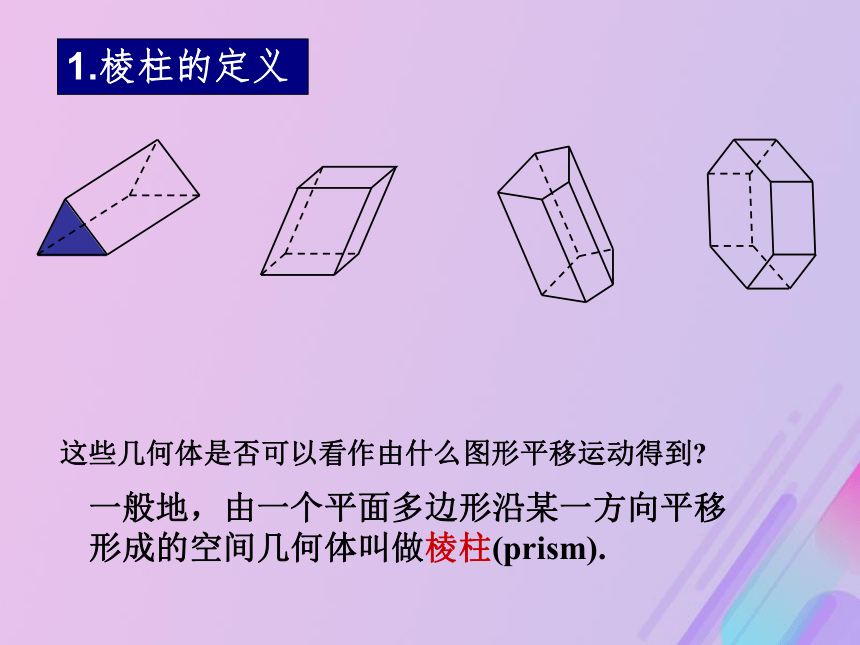
我们的生活息息相关.空间几何体是由哪些基本几何体组成的?如何描述和刻画这些几何体的形状和大小?构成这些几何体的基本元素之间具有怎样的位置关系?情境引入棱柱 棱锥 棱台1.棱柱的定义这些几何体是否可以看作由什么图形平移运动得到?一般地,由一个平面多边形沿某一方向平移
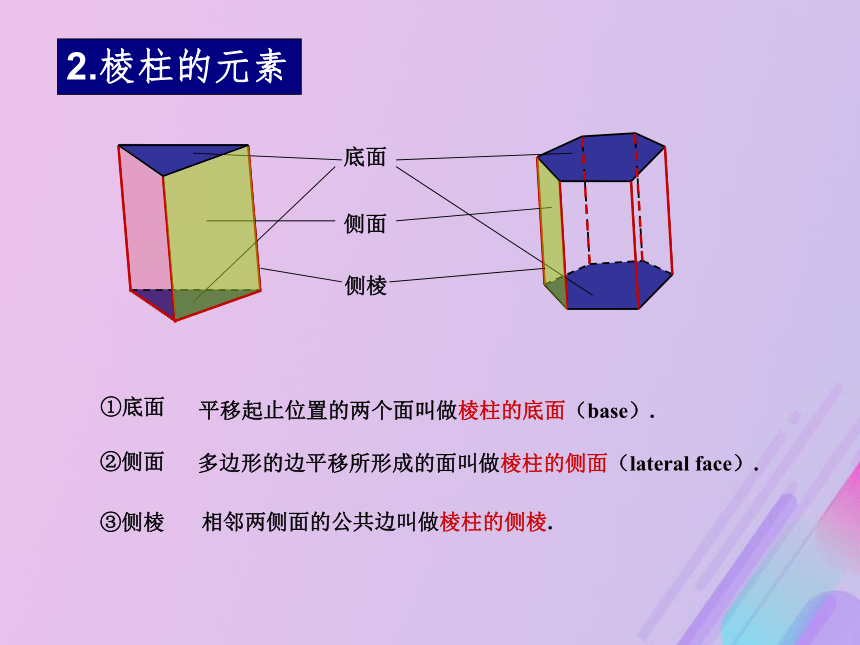
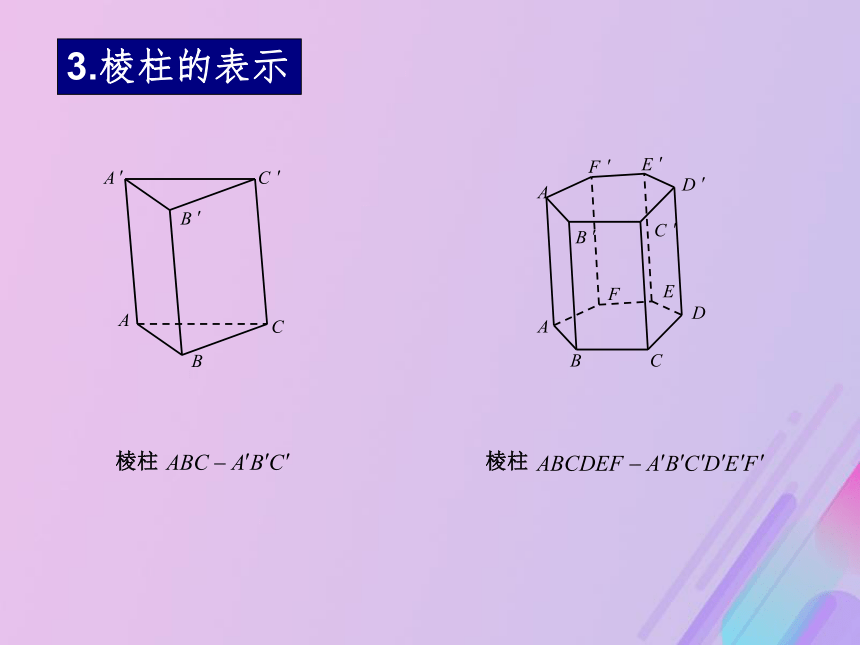
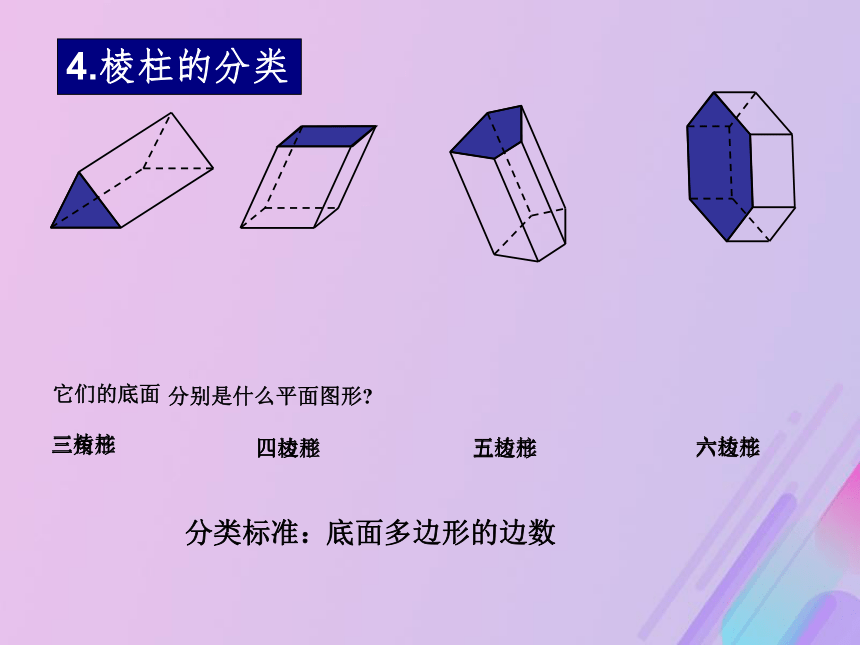
形成的空间几何体叫做棱柱(prism).底面侧棱侧面相邻两侧面的公共边叫做棱柱的侧棱.③侧棱 2.棱柱的元素①底面②侧面平移起止位置的两个面叫做棱柱的底面(base). 多边形的边平移所形成的面叫做棱柱的侧面(lateral face).3.棱柱的表示它们的底面三角形四边形五边形六边形底面多边形的边数三棱柱四棱柱五棱柱六棱柱4.棱柱的分类分类标准:分别是什么平面图形?观察下列几何体,回答①两个底面多边形间的关系?②上下底面对应边间的关系?
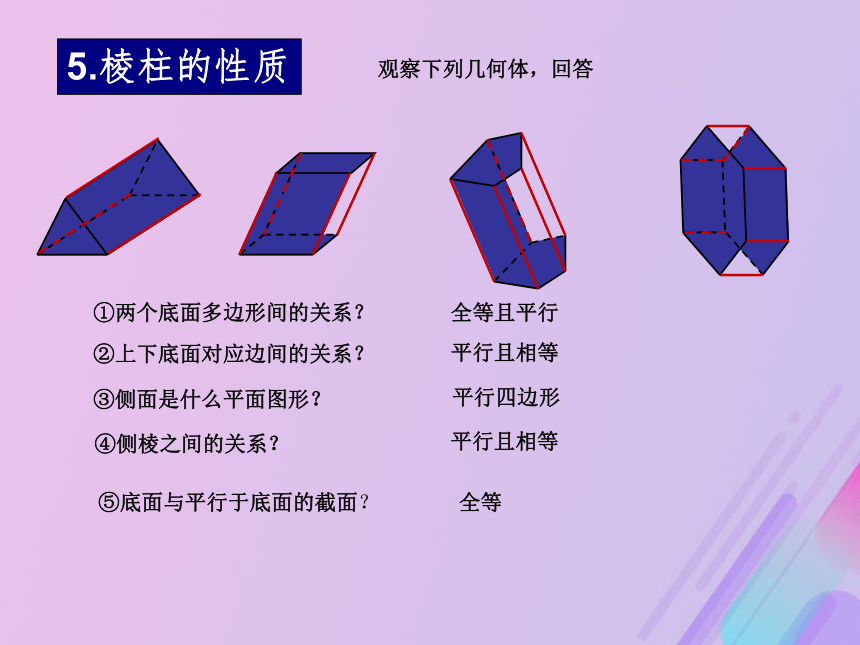
④侧棱之间的关系?③侧面是什么平面图形?全等且平行平行且相等平行且相等平行四边形5.棱柱的性质 ⑤底面与平行于底面的截面? 全等埃及卡夫拉王金字塔墨西哥太阳金字塔(二)棱锥的概念观察下图,如何将棱柱变换成下方的几何体?1.棱锥的定义当棱柱的一个底面收缩为一个点时,得到的几何体
叫做棱锥(pyramid).类比棱柱,给棱锥各元素命名底面侧面侧棱相邻两侧面
的公共边底面侧面侧棱相邻两侧面
的公共边顶点由棱柱的一个
底面收缩而成2.棱锥的元素观察下列棱锥,归纳它们的底面和侧面各有什么特征?棱锥的性质:①底面是多边形(如三角形、四边形、五边形等)在同一个棱锥中的各个侧面三角形有什么共同特征?②侧面是三角形有一个公共顶点的3.棱锥的性质思考题:能否类比棱柱的表示法与分类给出棱锥的表示法与分类?(三)棱台的概念1.棱台的定义观察下图,如何将棱锥变换成下方的几何体?棱锥被平行于底面的一个平面所截后,截面和底面之间
的部分叫做棱台(truncated pyramid).侧面侧棱上底面下底面2.棱台的元素①两个底面多边形间的关系?②上下底面对应边间的关系?
④侧棱之间的关系?③侧面是什么平面图形?相似平行不等延长后交于一点梯形概念辨析:1.下图中的几何体是不是棱台?为什么?学生活动线段平行四边形三角形梯形平面多边形棱柱棱锥棱台回顾反思两个底面是全
等多边形且对
应边互相平行互相平行
且相等平行四边形一底面是多边形,
另一底面缩为一点有一个公共顶
点的三角形交于一点梯形上下底面平行,是相似多边形延长后交于一点由若干个平面多边形围成的几何体叫做多面体(polyhedron).棱柱、棱锥、棱台都是由一些平面多边形围成的几何体.食盐晶体明矾晶体石膏晶体(四)多面体思考:多面体至少有几个面?这个多面体是怎样的几何体?四棱锥动动手(1)画一个四棱柱①画上底面——画一个四边形②画侧棱——从四边形的每一个顶点
画平行且相等的线段③画下底面——顺次连结这些线段的
另一个端点注意:被挡住的线要画成虚线.数学运用(2)画一个三棱台①画一个三棱锥②在侧棱上任取一点,从这点开始,
顺次在各个侧面内画出与底面
对应边平行的线段③将多余的线段擦去数学运用练一练:以三角形ABC为底面画一个三棱柱.数学运用1.判断:
⑴三棱柱是指有三条棱的几何体 ( )
⑵由四个面围成的几何体只能是三棱锥,
由五个面围成的几何体只能是四棱锥 ( )
⑶棱锥的侧面只能是三角形 ( )
⑷棱柱的每一个面都不会是三角形 ( )
⑸棱台的侧面一定不会是平行四边形 ( )
⑹有一个面是多边形,其余各面都是三角形的几何
体是棱锥. ( )课堂练习2.有两个面互相平行,其余各面都是平行四边形的几何体是不是棱柱?课堂练习 3.如图,四棱柱的六个面都是平行四边形, 这个四棱柱可以由哪几个平面图形按怎样的方向平移得到?课堂练习(1)棱柱、棱锥、棱台的定义和性质
(2)运动变化、类比联想的观点
(3)将空间问题转化成平面问题的转化思想回顾小结课外作业请同学们课后找一找生活中具有棱柱、棱锥和棱台几何结构特征的实物.
我们的生活息息相关.空间几何体是由哪些基本几何体组成的?如何描述和刻画这些几何体的形状和大小?构成这些几何体的基本元素之间具有怎样的位置关系?情境引入棱柱 棱锥 棱台1.棱柱的定义这些几何体是否可以看作由什么图形平移运动得到?一般地,由一个平面多边形沿某一方向平移
形成的空间几何体叫做棱柱(prism).底面侧棱侧面相邻两侧面的公共边叫做棱柱的侧棱.③侧棱 2.棱柱的元素①底面②侧面平移起止位置的两个面叫做棱柱的底面(base). 多边形的边平移所形成的面叫做棱柱的侧面(lateral face).3.棱柱的表示它们的底面三角形四边形五边形六边形底面多边形的边数三棱柱四棱柱五棱柱六棱柱4.棱柱的分类分类标准:分别是什么平面图形?观察下列几何体,回答①两个底面多边形间的关系?②上下底面对应边间的关系?
④侧棱之间的关系?③侧面是什么平面图形?全等且平行平行且相等平行且相等平行四边形5.棱柱的性质 ⑤底面与平行于底面的截面? 全等埃及卡夫拉王金字塔墨西哥太阳金字塔(二)棱锥的概念观察下图,如何将棱柱变换成下方的几何体?1.棱锥的定义当棱柱的一个底面收缩为一个点时,得到的几何体
叫做棱锥(pyramid).类比棱柱,给棱锥各元素命名底面侧面侧棱相邻两侧面
的公共边底面侧面侧棱相邻两侧面
的公共边顶点由棱柱的一个
底面收缩而成2.棱锥的元素观察下列棱锥,归纳它们的底面和侧面各有什么特征?棱锥的性质:①底面是多边形(如三角形、四边形、五边形等)在同一个棱锥中的各个侧面三角形有什么共同特征?②侧面是三角形有一个公共顶点的3.棱锥的性质思考题:能否类比棱柱的表示法与分类给出棱锥的表示法与分类?(三)棱台的概念1.棱台的定义观察下图,如何将棱锥变换成下方的几何体?棱锥被平行于底面的一个平面所截后,截面和底面之间
的部分叫做棱台(truncated pyramid).侧面侧棱上底面下底面2.棱台的元素①两个底面多边形间的关系?②上下底面对应边间的关系?
④侧棱之间的关系?③侧面是什么平面图形?相似平行不等延长后交于一点梯形概念辨析:1.下图中的几何体是不是棱台?为什么?学生活动线段平行四边形三角形梯形平面多边形棱柱棱锥棱台回顾反思两个底面是全
等多边形且对
应边互相平行互相平行
且相等平行四边形一底面是多边形,
另一底面缩为一点有一个公共顶
点的三角形交于一点梯形上下底面平行,是相似多边形延长后交于一点由若干个平面多边形围成的几何体叫做多面体(polyhedron).棱柱、棱锥、棱台都是由一些平面多边形围成的几何体.食盐晶体明矾晶体石膏晶体(四)多面体思考:多面体至少有几个面?这个多面体是怎样的几何体?四棱锥动动手(1)画一个四棱柱①画上底面——画一个四边形②画侧棱——从四边形的每一个顶点
画平行且相等的线段③画下底面——顺次连结这些线段的
另一个端点注意:被挡住的线要画成虚线.数学运用(2)画一个三棱台①画一个三棱锥②在侧棱上任取一点,从这点开始,
顺次在各个侧面内画出与底面
对应边平行的线段③将多余的线段擦去数学运用练一练:以三角形ABC为底面画一个三棱柱.数学运用1.判断:
⑴三棱柱是指有三条棱的几何体 ( )
⑵由四个面围成的几何体只能是三棱锥,
由五个面围成的几何体只能是四棱锥 ( )
⑶棱锥的侧面只能是三角形 ( )
⑷棱柱的每一个面都不会是三角形 ( )
⑸棱台的侧面一定不会是平行四边形 ( )
⑹有一个面是多边形,其余各面都是三角形的几何
体是棱锥. ( )课堂练习2.有两个面互相平行,其余各面都是平行四边形的几何体是不是棱柱?课堂练习 3.如图,四棱柱的六个面都是平行四边形, 这个四棱柱可以由哪几个平面图形按怎样的方向平移得到?课堂练习(1)棱柱、棱锥、棱台的定义和性质
(2)运动变化、类比联想的观点
(3)将空间问题转化成平面问题的转化思想回顾小结课外作业请同学们课后找一找生活中具有棱柱、棱锥和棱台几何结构特征的实物.
