2018年高中数学第1章立体几何初步1.2.3直线与平面的位置关系课件8苏教版必修2(17张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.3直线与平面的位置关系课件8苏教版必修2(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 136.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 10:50:34 | ||
图片预览




文档简介
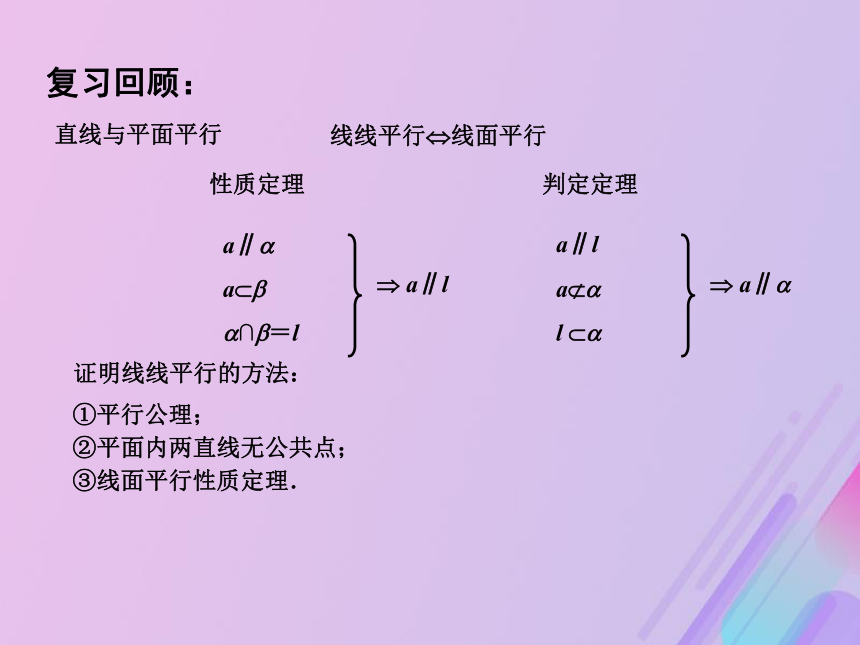
课件17张PPT。 1.2.3直线与平面的位置关系复习回顾:a∥? ? a∥la???∩?=l直线与平面平行性质定理a∥l? a∥?a??l ??判定定理线线平行?线面平行证明线线平行的方法:①平行公理;
②平面内两直线无公共点;
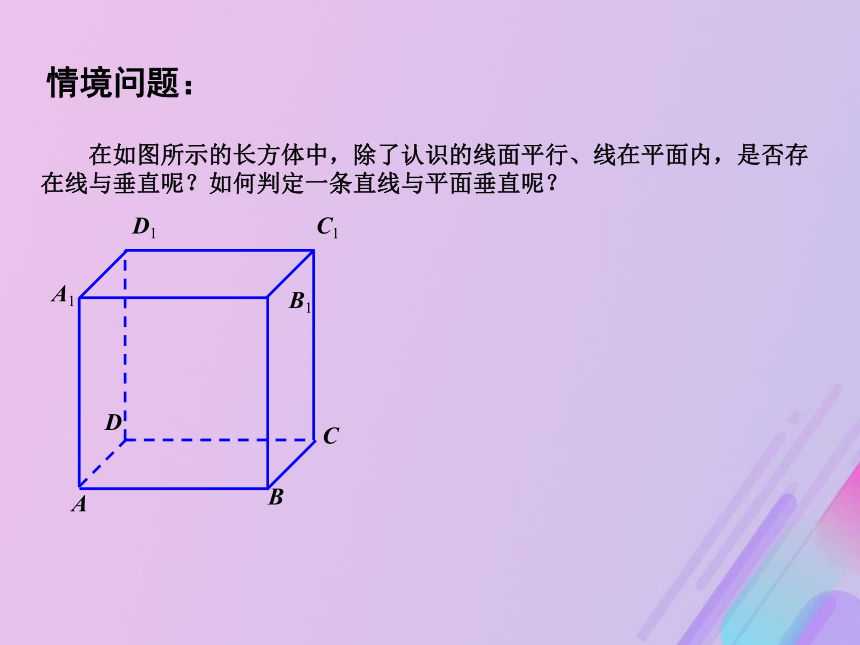
③线面平行性质定理. 情境问题: 在如图所示的长方体中,除了认识的线面平行、线在平面内,是否存在线与垂直呢?如何判定一条直线与平面垂直呢?ABCDA1B1C1D1直线与平面垂直的定义:
如果一条直线a与一个平面?内的任意一条直线都垂直,则称直线a与平面?互相垂直.
记作:a⊥?.
a —— 平面?的垂线;
? —— 直线a的垂面;
P —— 垂足.
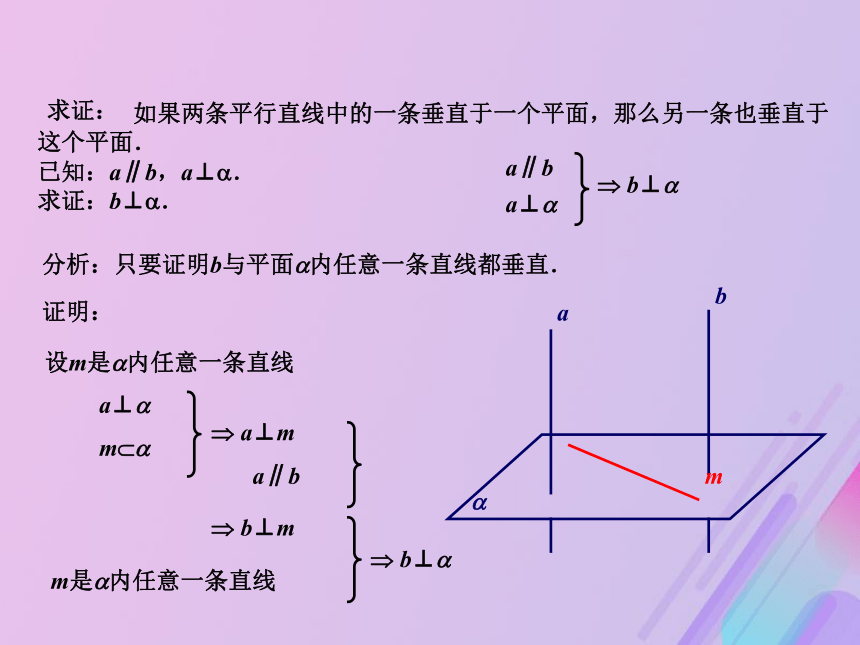
a⊥?,l?? ? a⊥l.?数学建构: 如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
已知:a∥b,a⊥?.
求证:b⊥?. 求证:a∥b? b⊥??aba⊥?分析:只要证明b与平面?内任意一条直线都垂直. 证明:设m是?内任意一条直线a⊥?m??? a⊥ma∥b? b⊥mm是?内任意一条直线? b⊥? 在如图所示的长方体中,过A点有且只有棱AA1与底面AC垂直. 同样,过A点也有且只有底面AC与棱AA1垂直. 思考:为什么说棱AA1与底面AC垂直?图中棱AA1与底面AC中的哪些线垂直?数学建构:在空间:
(1) 过一点有且只有一条直线与已知平面垂直;
(2) 过一点有且只有一个平面与已知直线垂直. 若正方体的棱长为2,则点A1到底面的距离是 .2从平面外一点引平面的垂线,这个点与垂足之间的距离,叫做这
个点到这个平面的距离. 直线与平面垂直的判定定理:
如果一条直线和一个平面内的两条相交直线垂直,那么这条直线
垂直于这个平面.? a⊥?线线垂直 ? 线面垂直m∩n=An??m??a⊥na⊥mA?amn数学建构:例1.已知四棱锥P-ABCD的底面是矩形,PA⊥AB,PA⊥AC,M、N分别是AB、PC的中点, (1)证明:BC⊥面PAB;(2)求证:MN⊥AB. 数学应用:练习:如图,在正方体ABCD-A1B1C1D1中,求证:AC⊥BD1. 数学应用: 思考:如图,正方体中,与底面ABCD垂直的棱有哪几条,它们之间有什么关系呢?直线与平面垂直的性质定理:
如果两条直线垂直于同一个平面,那么这两条直线平行.? a∥b线面垂直?线线平行b⊥?a⊥??ab数学建构:例2.已知直线l∥平面?,求证:直线l上各点到平面?的距离相等. 数学应用:?lPP?QQ?数学建构: 一条直线与一个平面平行,这条直线上任意一点到这个平面的距离,叫做这条直线和这个平面的距离. 1.下列说法中正确的有 .
①如果一条直线垂直于一个平面内的无数条直线,那么这条直线就与这个平面垂直.
②过一点有且只有一条直线和已知直线垂直.
③若A,B两点到平面?的距离相等,则直线AB∥?.
④已知直线a在平面?内,若l⊥? ,则l⊥?.
⑤已知直线l和平面? ,若l⊥? ,则l和?相交. 数学应用:2.若AB的中点到平面?的距离为4cm,点A到平面?的距离为6cm,则点B到平面?的距离为_______cm. 数学应用:3.如图,已知PA⊥?,PB⊥?,垂足分别为A、B,且?∩?=l,
求证:l⊥平面PAB. 4.在三棱锥A—BCD中,AB=AD,CB=CD,求证:AC⊥BD.ABCDE5.能否构造出一个三棱锥A-BCD,使它的四个面均为直角三角形?ABCD作Rt△BCD,使∠C=90?,过顶点B(D)作BA⊥面BCD,连AC,AD,则三棱锥A-BCD为所求作的.数学应用:小结:直线与平面垂直的定义直线与平面垂直的判定定义定理线面垂直?线线垂直线面垂直?线线平行1.知识点2.方法3.数学思想类比点到平面的距离直线和平面间的距离
②平面内两直线无公共点;
③线面平行性质定理. 情境问题: 在如图所示的长方体中,除了认识的线面平行、线在平面内,是否存在线与垂直呢?如何判定一条直线与平面垂直呢?ABCDA1B1C1D1直线与平面垂直的定义:
如果一条直线a与一个平面?内的任意一条直线都垂直,则称直线a与平面?互相垂直.
记作:a⊥?.
a —— 平面?的垂线;
? —— 直线a的垂面;
P —— 垂足.
a⊥?,l?? ? a⊥l.?数学建构: 如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面.
已知:a∥b,a⊥?.
求证:b⊥?. 求证:a∥b? b⊥??aba⊥?分析:只要证明b与平面?内任意一条直线都垂直. 证明:设m是?内任意一条直线a⊥?m??? a⊥ma∥b? b⊥mm是?内任意一条直线? b⊥? 在如图所示的长方体中,过A点有且只有棱AA1与底面AC垂直. 同样,过A点也有且只有底面AC与棱AA1垂直. 思考:为什么说棱AA1与底面AC垂直?图中棱AA1与底面AC中的哪些线垂直?数学建构:在空间:
(1) 过一点有且只有一条直线与已知平面垂直;
(2) 过一点有且只有一个平面与已知直线垂直. 若正方体的棱长为2,则点A1到底面的距离是 .2从平面外一点引平面的垂线,这个点与垂足之间的距离,叫做这
个点到这个平面的距离. 直线与平面垂直的判定定理:
如果一条直线和一个平面内的两条相交直线垂直,那么这条直线
垂直于这个平面.? a⊥?线线垂直 ? 线面垂直m∩n=An??m??a⊥na⊥mA?amn数学建构:例1.已知四棱锥P-ABCD的底面是矩形,PA⊥AB,PA⊥AC,M、N分别是AB、PC的中点, (1)证明:BC⊥面PAB;(2)求证:MN⊥AB. 数学应用:练习:如图,在正方体ABCD-A1B1C1D1中,求证:AC⊥BD1. 数学应用: 思考:如图,正方体中,与底面ABCD垂直的棱有哪几条,它们之间有什么关系呢?直线与平面垂直的性质定理:
如果两条直线垂直于同一个平面,那么这两条直线平行.? a∥b线面垂直?线线平行b⊥?a⊥??ab数学建构:例2.已知直线l∥平面?,求证:直线l上各点到平面?的距离相等. 数学应用:?lPP?QQ?数学建构: 一条直线与一个平面平行,这条直线上任意一点到这个平面的距离,叫做这条直线和这个平面的距离. 1.下列说法中正确的有 .
①如果一条直线垂直于一个平面内的无数条直线,那么这条直线就与这个平面垂直.
②过一点有且只有一条直线和已知直线垂直.
③若A,B两点到平面?的距离相等,则直线AB∥?.
④已知直线a在平面?内,若l⊥? ,则l⊥?.
⑤已知直线l和平面? ,若l⊥? ,则l和?相交. 数学应用:2.若AB的中点到平面?的距离为4cm,点A到平面?的距离为6cm,则点B到平面?的距离为_______cm. 数学应用:3.如图,已知PA⊥?,PB⊥?,垂足分别为A、B,且?∩?=l,
求证:l⊥平面PAB. 4.在三棱锥A—BCD中,AB=AD,CB=CD,求证:AC⊥BD.ABCDE5.能否构造出一个三棱锥A-BCD,使它的四个面均为直角三角形?ABCD作Rt△BCD,使∠C=90?,过顶点B(D)作BA⊥面BCD,连AC,AD,则三棱锥A-BCD为所求作的.数学应用:小结:直线与平面垂直的定义直线与平面垂直的判定定义定理线面垂直?线线垂直线面垂直?线线平行1.知识点2.方法3.数学思想类比点到平面的距离直线和平面间的距离
