2018年高中数学第1章立体几何初步1.3空间几何体的表面积和体积课件1苏教版必修2(39张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.3空间几何体的表面积和体积课件1苏教版必修2(39张) |

|
|
| 格式 | zip | ||
| 文件大小 | 487.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览







文档简介
课件39张PPT。1.3 简单几何体的表面积和体积回忆复习有关概念1、直棱柱:2、正棱柱:3、正棱锥:4、正棱台:侧棱和底面垂直的棱柱叫直棱柱底面是正多边形的直棱柱叫正棱柱底面是正多边形,顶点在底面的射影是底面中心
的棱锥正棱锥被平行于底面的平面所截,
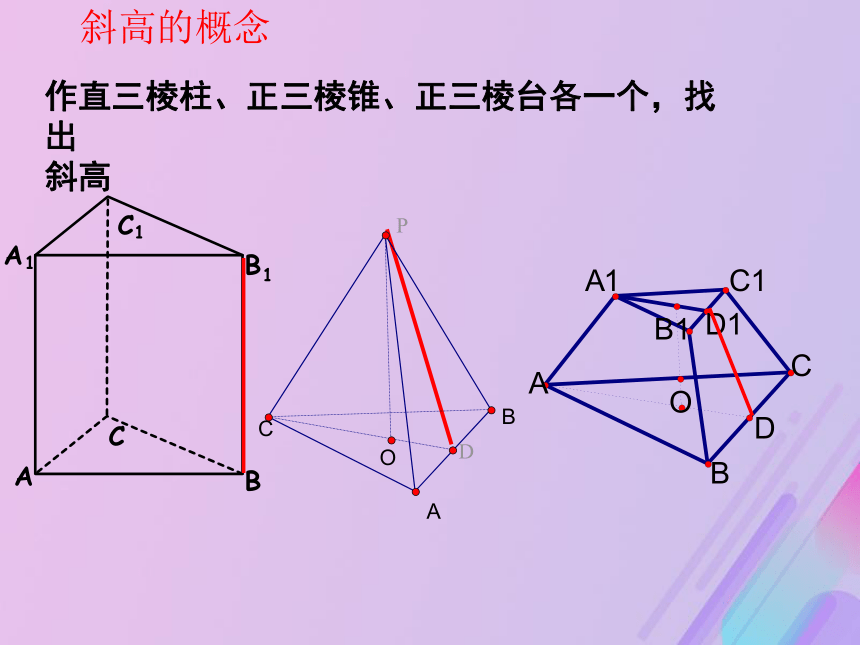
截面和底面之间的部分叫正棱台作直三棱柱、正三棱锥、正三棱台各一个,找出
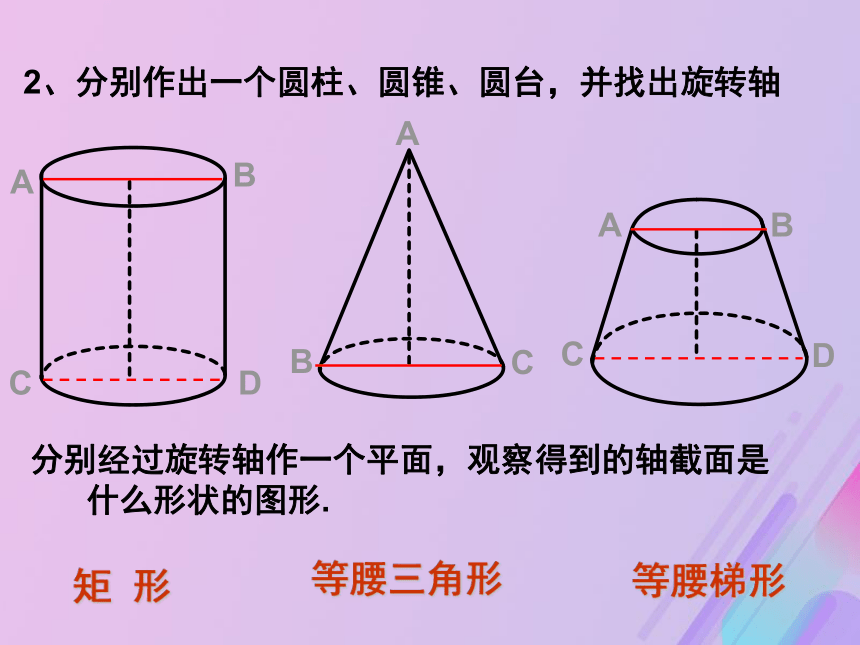
斜高斜高的概念2、分别作出一个圆柱、圆锥、圆台,并找出旋转轴分别经过旋转轴作一个平面,观察得到的轴截面是
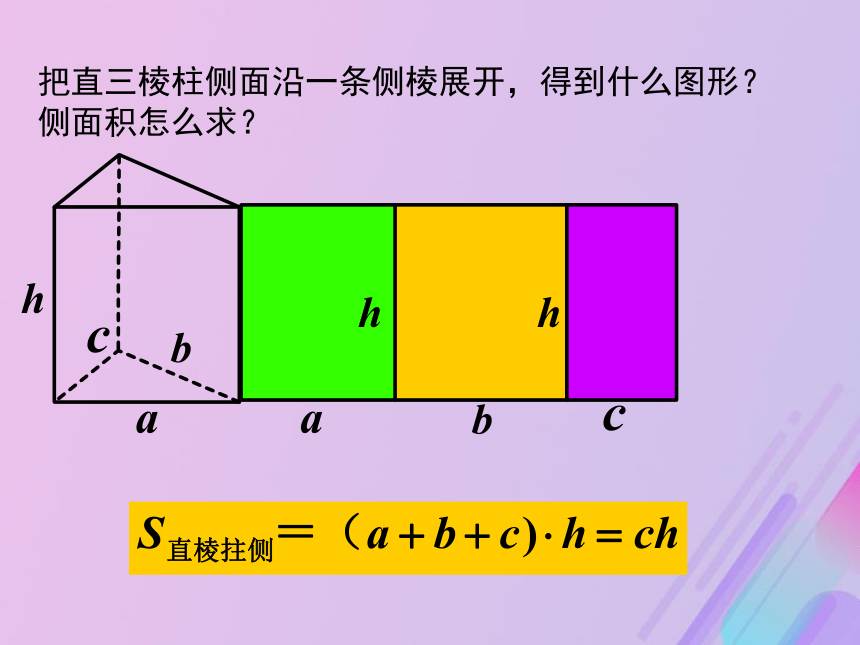
什么形状的图形.矩 形等腰三角形等腰梯形①直棱柱:设棱柱的高为h,底面多边形的周长为c,则
S直棱柱侧= .
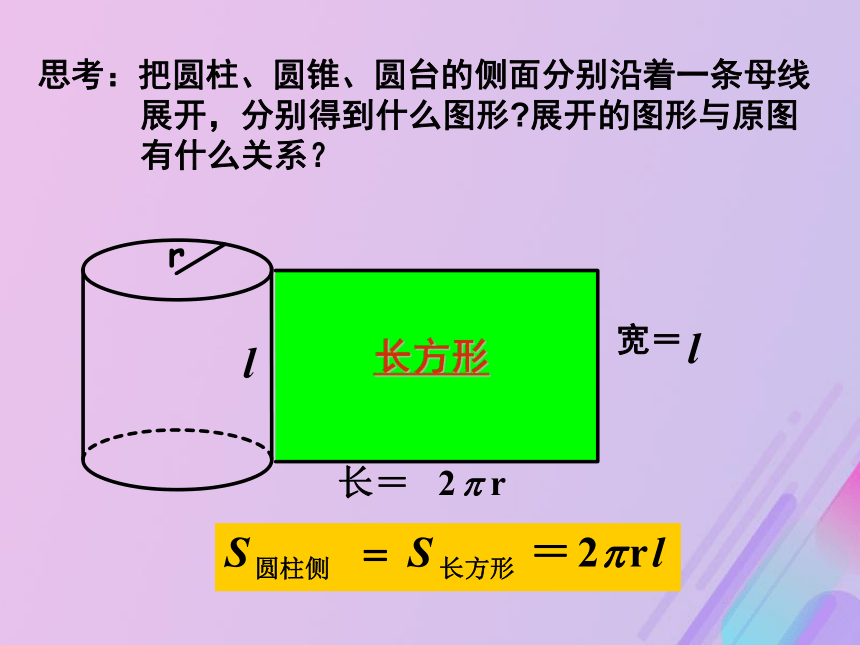
②圆柱:如果圆柱的底面半径为r,母线长为l,那么
S圆柱侧= .
ch2πrl知识点一:柱、锥、台、球的表面积与侧面积(1)柱体的侧面积把直三棱柱侧面沿一条侧棱展开,得到什么图形?
侧面积怎么求?思考:把圆柱、圆锥、圆台的侧面分别沿着一条母线
展开,分别得到什么图形?展开的图形与原图
有什么关系?长方形①正棱锥:设正棱锥底面正多边形的周长为c,斜高为h′,则
S正棱锥侧= .
②圆锥:如果圆锥的底面半径为r,母线长为l,那么
S圆锥侧= .
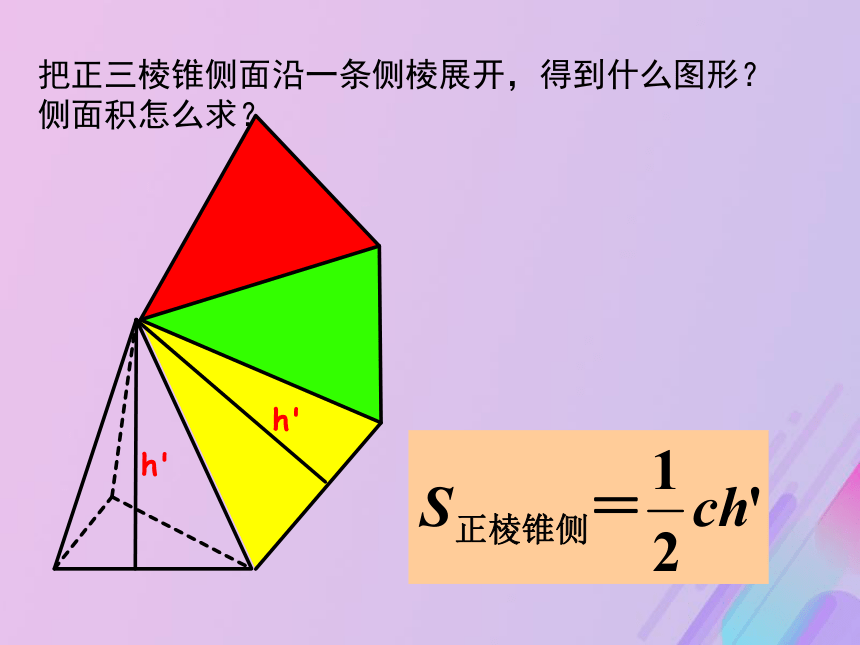
1∕2ch′πrl(2)锥体的侧面积把正三棱锥侧面沿一条侧棱展开,得到什么图形?
侧面积怎么求?思考:把圆柱、圆锥、圆台的侧面分别沿着一条母线
展开,分别得到什么图形?展开的图形与原图
有什么关系?扇形
①正棱台:设正n棱台的上底面、下底面周长分别为c′、c,斜高为h′,则正n棱台的侧面积公式:S正棱台侧= .
②圆台:如果圆台的上、下底面半径分别为r′、r,母线长为l,则S圆台侧= .
1∕2(c+c′)h′πl(r′+r)(3)台体的侧面积注:表面积=侧面积+底面积.把正三棱台侧面沿一条侧棱展开,得到什么图形?
侧面积怎么求?思考:把圆柱、圆锥、圆台的侧面分别沿着一条母线
展开,分别得到什么图形?展开的图形与原图
有什么关系?扇环例1:一个正三棱台的上、下底面边长分别是3cm和6cm,高是3/2cm,求三棱台的侧面积. 分析:关键是求出斜高,注意图中的直角梯形O1ODD1E例3:圆台的上、下底面半径分别为2和4,高为 ,求其侧面展开图扇环所对的圆心角分析:抓住相似三角形中的相似比是解题的关键小结:1、抓住侧面展开图的形状,用好相应的计算公式,注意逆向用公式;
2、圆台问题恢复成圆锥图形在圆锥中解决圆台问题,注意相似比.答:1800例:圆台的上、下底半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是1800,那么圆台的侧面积是多少?(结果中保留π)小结:1、弄清楚柱、锥、台的侧面展开图的形状是关键;
2、对应的面积公式例1:一个正三棱柱的底面是边长为5的正三角形,侧棱长为4,则其侧面积为 ______;答:60例2:正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一个小棱锥和一个棱台,求棱台的侧面积 例3 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 .BCAS 分析:四面体的展开图是由四个全等的正三角形组成.因此,四面体S-ABC 的表面积.交BC于点D.例4(2010年广东省惠州市高三调研)如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D,E是CC1,BC的中点,AE=DE.
(1)求此正三棱柱的侧棱长;
(2)正三棱柱ABC-A1B1C1的表面积.
【思路点拨】 (1)证明△AED为直角三角形,然后求侧棱长;(2)分别求出侧面积与底面积.
【点评】 求表面积应分别求各部分面的面积,所以应弄清图形的形状,利用相应的公式求面积,规则的图形可直接求,不规则的图形往往要再进行转化,常分割成几部分来求.
思考:怎样求斜棱柱的侧面积?
1)侧面展开图是——
平行四边形
2)S斜棱柱侧=直截面周长×侧棱长
3) S侧=所有侧面面积之和1.高考中对几何体的表面积的考查一般在客观题中,借以考查空间想象能力和运算能力,只要正确把握几何体的结构,准确应用面积公式,就可以顺利解决.
几何体的表面积问题小结2.多面体的表面积是各个面的面积之和.圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.
3.几何体的表面积应注意重合部分的处理.
(1)长方体的体积
V长方体=abc= .
(其中a、b、c为长、宽、高,S为底面积,h为高)
(2)柱体(圆柱和棱柱)的体积
V柱体=Sh.
其中,V圆柱=πr2h(其中r为底面半径).
Sh知识点二.柱、锥、台、球的体积(3)锥体(圆锥和棱锥)的体积
V锥体= Sh.
其中V圆锥= , r为底面半径.1∕3πr2h(4)台体的体积公式
V台=h(S++S′).
注:h为台体的高,S′和S分别为上下两个底面的面积.
其中V圆台= .
注:h为台体的高,r′、r分别为上、下两底的半径.
(5)球的体积
V球= .
1∕3πh(r2+rr′+r′2)1∕3πR3例 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD,求它的体积是正方体体积的几分之几?1.求空间几何体的体积除利用公式法外,还常用分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算问题的常用方法.
几何体的体积小结2.计算柱体、锥体、台体的体积关键是根据条件找出相应的底面面积和高,要充分利用多面体的截面及旋转体的轴截面,将空间问题转化为平面问题.
第一步:分割O球面被分割成n个网格,
表面积分别为:则球的表面积:则球的体积为:设“小锥体”的体积为:知识点三、球的表面积和体积(O第二步:求近似和O由第一步得:第三步:转化为球的表面积 如果网格分的越细,则:由①② 得:设球的半径为R,则球的体积公式为
V球= .
4∕3πR3例1.(2009年高考上海卷)若球O1、O2表面积之比=4,则它们的半径之比=______.
(1)若球的表面积变为原来的2倍,则半径变为原来的—倍。
(2)若球半径变为原来的2倍,则表面积变为原来的—倍。
(3)若两球表面积之比为1:2,则其体积之比是———。
(4)若两球体积之比是1:2,则其表面积之比是———。例2:例3.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系例4已知过球面上三点A、B、C的截面到球心O的距离等于球半径的一半,且AB=BC=CA=2cm,求球的体积,表面积.解:如图,设球O半径为R,
截面⊙O′的半径为r,例5、有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.作轴截面规律方法总结1.直棱柱的侧面展开图是一些矩形,正棱锥的侧面展开图是一些全等的等腰三角形,正棱台的侧面展开图是一些全等的等腰梯形.
2.斜棱柱的侧面积等于它的直截面(垂直于侧棱并与每条侧棱都相交的截面)的周长与侧棱长的乘积.
3.如果直棱柱的底面周长是c,高是h,那么它的侧面积是S直棱柱侧=ch.
4.应注意各个公式的推导过程,不要死记硬背公式本身,要熟悉柱体中的矩形、锥体中的直角三角形、台体中的直角梯形等特征图形在公式推导中的作用.
规律方法总结5.如果不是正棱柱、正棱锥、正棱台,在求其侧面积或全面积时,应对每一个侧面的面积分别求解后再相加.
6.求球的体积和表面积的关键是求出球的半径.反之,若已知球的表面积或体积,那么就可以得出其半径的大小.
7.计算组合体的体积时,首先要弄清楚它是由哪些基本几何体构成,然后再通过轴截面分析和解决问题.
8.计算圆柱、圆锥、圆台的体积时,关键是根据条件找出相应的底面面积和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解.
的棱锥正棱锥被平行于底面的平面所截,
截面和底面之间的部分叫正棱台作直三棱柱、正三棱锥、正三棱台各一个,找出
斜高斜高的概念2、分别作出一个圆柱、圆锥、圆台,并找出旋转轴分别经过旋转轴作一个平面,观察得到的轴截面是
什么形状的图形.矩 形等腰三角形等腰梯形①直棱柱:设棱柱的高为h,底面多边形的周长为c,则
S直棱柱侧= .
②圆柱:如果圆柱的底面半径为r,母线长为l,那么
S圆柱侧= .
ch2πrl知识点一:柱、锥、台、球的表面积与侧面积(1)柱体的侧面积把直三棱柱侧面沿一条侧棱展开,得到什么图形?
侧面积怎么求?思考:把圆柱、圆锥、圆台的侧面分别沿着一条母线
展开,分别得到什么图形?展开的图形与原图
有什么关系?长方形①正棱锥:设正棱锥底面正多边形的周长为c,斜高为h′,则
S正棱锥侧= .
②圆锥:如果圆锥的底面半径为r,母线长为l,那么
S圆锥侧= .
1∕2ch′πrl(2)锥体的侧面积把正三棱锥侧面沿一条侧棱展开,得到什么图形?
侧面积怎么求?思考:把圆柱、圆锥、圆台的侧面分别沿着一条母线
展开,分别得到什么图形?展开的图形与原图
有什么关系?扇形
①正棱台:设正n棱台的上底面、下底面周长分别为c′、c,斜高为h′,则正n棱台的侧面积公式:S正棱台侧= .
②圆台:如果圆台的上、下底面半径分别为r′、r,母线长为l,则S圆台侧= .
1∕2(c+c′)h′πl(r′+r)(3)台体的侧面积注:表面积=侧面积+底面积.把正三棱台侧面沿一条侧棱展开,得到什么图形?
侧面积怎么求?思考:把圆柱、圆锥、圆台的侧面分别沿着一条母线
展开,分别得到什么图形?展开的图形与原图
有什么关系?扇环例1:一个正三棱台的上、下底面边长分别是3cm和6cm,高是3/2cm,求三棱台的侧面积. 分析:关键是求出斜高,注意图中的直角梯形O1ODD1E例3:圆台的上、下底面半径分别为2和4,高为 ,求其侧面展开图扇环所对的圆心角分析:抓住相似三角形中的相似比是解题的关键小结:1、抓住侧面展开图的形状,用好相应的计算公式,注意逆向用公式;
2、圆台问题恢复成圆锥图形在圆锥中解决圆台问题,注意相似比.答:1800例:圆台的上、下底半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是1800,那么圆台的侧面积是多少?(结果中保留π)小结:1、弄清楚柱、锥、台的侧面展开图的形状是关键;
2、对应的面积公式例1:一个正三棱柱的底面是边长为5的正三角形,侧棱长为4,则其侧面积为 ______;答:60例2:正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一个小棱锥和一个棱台,求棱台的侧面积 例3 已知棱长为a,各面均为等边三角形的四面体S-ABC,求它的表面积 .BCAS 分析:四面体的展开图是由四个全等的正三角形组成.因此,四面体S-ABC 的表面积.交BC于点D.例4(2010年广东省惠州市高三调研)如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D,E是CC1,BC的中点,AE=DE.
(1)求此正三棱柱的侧棱长;
(2)正三棱柱ABC-A1B1C1的表面积.
【思路点拨】 (1)证明△AED为直角三角形,然后求侧棱长;(2)分别求出侧面积与底面积.
【点评】 求表面积应分别求各部分面的面积,所以应弄清图形的形状,利用相应的公式求面积,规则的图形可直接求,不规则的图形往往要再进行转化,常分割成几部分来求.
思考:怎样求斜棱柱的侧面积?
1)侧面展开图是——
平行四边形
2)S斜棱柱侧=直截面周长×侧棱长
3) S侧=所有侧面面积之和1.高考中对几何体的表面积的考查一般在客观题中,借以考查空间想象能力和运算能力,只要正确把握几何体的结构,准确应用面积公式,就可以顺利解决.
几何体的表面积问题小结2.多面体的表面积是各个面的面积之和.圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.
3.几何体的表面积应注意重合部分的处理.
(1)长方体的体积
V长方体=abc= .
(其中a、b、c为长、宽、高,S为底面积,h为高)
(2)柱体(圆柱和棱柱)的体积
V柱体=Sh.
其中,V圆柱=πr2h(其中r为底面半径).
Sh知识点二.柱、锥、台、球的体积(3)锥体(圆锥和棱锥)的体积
V锥体= Sh.
其中V圆锥= , r为底面半径.1∕3πr2h(4)台体的体积公式
V台=h(S++S′).
注:h为台体的高,S′和S分别为上下两个底面的面积.
其中V圆台= .
注:h为台体的高,r′、r分别为上、下两底的半径.
(5)球的体积
V球= .
1∕3πh(r2+rr′+r′2)1∕3πR3例 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD,求它的体积是正方体体积的几分之几?1.求空间几何体的体积除利用公式法外,还常用分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算问题的常用方法.
几何体的体积小结2.计算柱体、锥体、台体的体积关键是根据条件找出相应的底面面积和高,要充分利用多面体的截面及旋转体的轴截面,将空间问题转化为平面问题.
第一步:分割O球面被分割成n个网格,
表面积分别为:则球的表面积:则球的体积为:设“小锥体”的体积为:知识点三、球的表面积和体积(O第二步:求近似和O由第一步得:第三步:转化为球的表面积 如果网格分的越细,则:由①② 得:设球的半径为R,则球的体积公式为
V球= .
4∕3πR3例1.(2009年高考上海卷)若球O1、O2表面积之比=4,则它们的半径之比=______.
(1)若球的表面积变为原来的2倍,则半径变为原来的—倍。
(2)若球半径变为原来的2倍,则表面积变为原来的—倍。
(3)若两球表面积之比为1:2,则其体积之比是———。
(4)若两球体积之比是1:2,则其表面积之比是———。例2:例3.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系例4已知过球面上三点A、B、C的截面到球心O的距离等于球半径的一半,且AB=BC=CA=2cm,求球的体积,表面积.解:如图,设球O半径为R,
截面⊙O′的半径为r,例5、有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.作轴截面规律方法总结1.直棱柱的侧面展开图是一些矩形,正棱锥的侧面展开图是一些全等的等腰三角形,正棱台的侧面展开图是一些全等的等腰梯形.
2.斜棱柱的侧面积等于它的直截面(垂直于侧棱并与每条侧棱都相交的截面)的周长与侧棱长的乘积.
3.如果直棱柱的底面周长是c,高是h,那么它的侧面积是S直棱柱侧=ch.
4.应注意各个公式的推导过程,不要死记硬背公式本身,要熟悉柱体中的矩形、锥体中的直角三角形、台体中的直角梯形等特征图形在公式推导中的作用.
规律方法总结5.如果不是正棱柱、正棱锥、正棱台,在求其侧面积或全面积时,应对每一个侧面的面积分别求解后再相加.
6.求球的体积和表面积的关键是求出球的半径.反之,若已知球的表面积或体积,那么就可以得出其半径的大小.
7.计算组合体的体积时,首先要弄清楚它是由哪些基本几何体构成,然后再通过轴截面分析和解决问题.
8.计算圆柱、圆锥、圆台的体积时,关键是根据条件找出相应的底面面积和高,应注意充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解.
