2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件5苏教版必修2(17张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件5苏教版必修2(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 287.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览





文档简介
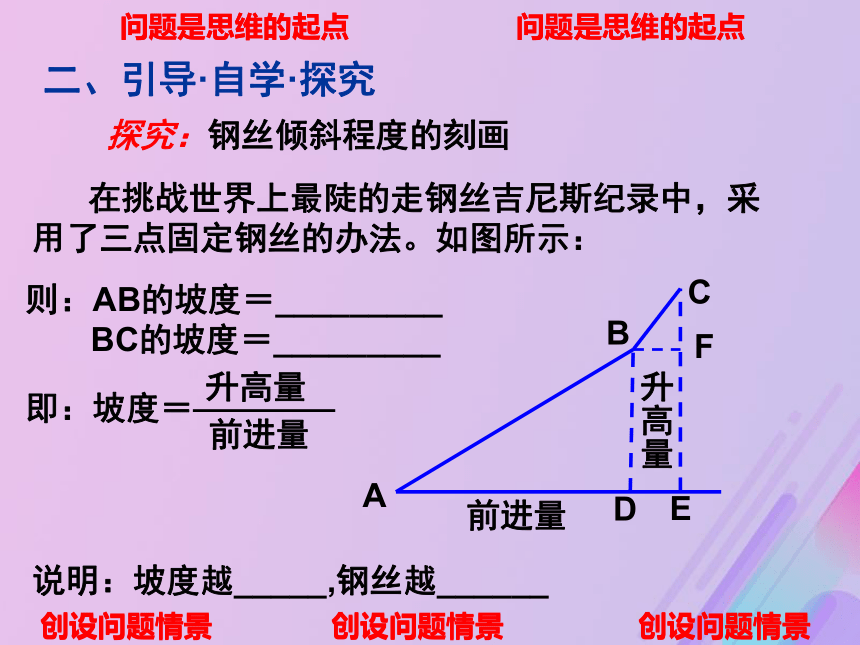
课件17张PPT。2.1.1直线的斜率(第一课时) 问题是思维的起点 问题是思维的起点 问题是思维的起点 问题是思维的起点 创设问题情景 创设问题情景 创设问题情景 创设问题情景 创设问题情景 创设问题情景一、创设问题情境 ——问题是思维的起点 问题1:视频中挑战吉尼斯纪录,高空走钢丝,惊险刺激,扣人心弦,中国维吾尔族勇士阿布来提·麦君挑战的是什么样的吉尼斯纪录?问题2:什么叫“陡”?用什么方法刻画钢丝绳陡峭的程度? 在挑战世界上最陡的走钢丝吉尼斯纪录中,采用了三点固定钢丝的办法。如图所示: 问题是思维的起点 问题是思维的起点 问题是思维的起点 问题是思维的起点 创设问题情景 创设问题情景 创设问题情景 创设问题情景 创设问题情景 创设问题情景二、引导·自学·探究 探究:钢丝倾斜程度的刻画升高量 前进量 则:AB的坡度=_________
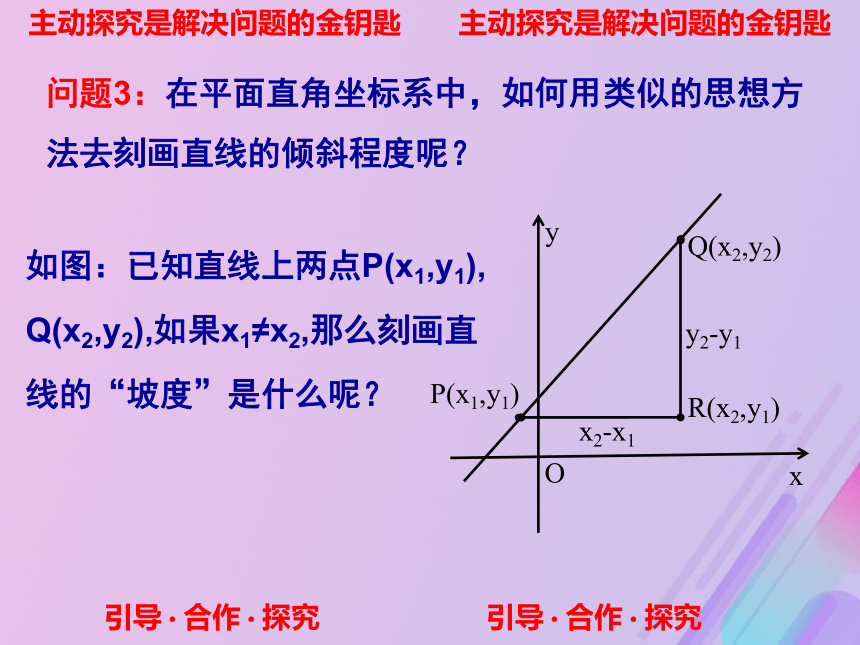
BC的坡度=_________即:坡度=说明:坡度越_____,钢丝越______主动探究是解决问题的金钥匙 主动探究是解决问题的金钥匙 引导·合作·探究 引导·合作·探究 问题3:在平面直角坐标系中,如何用类似的思想方法去刻画直线的倾斜程度呢?如图:已知直线上两点P(x1,y1),
Q(x2,y2),如果x1≠x2,那么刻画直
线的“坡度”是什么呢?y2-y1x2-x1 引导·合作·探究 引导·合作·探究直线斜率的定义:主动探究是解决问题的金钥匙 主动探究是解决问题的金钥匙已知直线上两点P(x1,y1),Q(x2,y2),如果x1≠x2,
则直线PQ的斜率为:形数斜率为0,这时直线PQ平行于x轴或与x轴重合。(2)如果y1=y2,则直线PQ的斜率怎样?(1)如果x1=x2,则直线PQ的斜率怎样? 引导·合作·探究 引导·合作·探究主动探究是解决问题的金钥匙 主动探究是解决问题的金钥匙问题4:研究特例:斜率不存在,这时直线PQ垂直于x轴联想、拓展、引申 联想、拓展、引申问题5:斜率公式的结构如何?下标的次序能否改变?联想、拓展、引申 联想、拓展、引申y2-y1=△yx2-x1=△xy2-y1x2-x1联想、拓展、引申 联想、拓展、引申问题6:联想、拓展、引申 联想、拓展、引申 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固(三)应用、激活、巩固 ——小试牛刀,轻松过关应用·激活·巩固 应用·激活·巩固应用·激活·巩固 应用·激活·巩固例1、如图,直线l1、l2、l3、l4都经过P(3,2),又l1、l2、
l3、l4分别经过A(-1,0)、B(5,-2)、C(-2,2)、D(3,4)。
讨论直线l1、l2、l3、l4的斜率是否存在,若存在,
求出直线的斜率解:设直线l1、l2、l3、l4的斜率分别为k1、k2、k3、k4,则:直线从左下方向右上方倾斜k>0直线从左上方向右下方倾斜k<0联想、拓展、引申 联想、拓展、引申题后反思,联想拓展 —思一思,想一想,你能有更大的进步联想、拓展、引申 联想、拓展、引申问题7:直线的方向与斜率之间有何对应关系?12k=0直线与x轴平行或重合3k不存在直线垂直于x 轴4 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固(三)应用、激活、巩固 ——小试牛刀,轻松过关应用·激活·巩固 应用·激活·巩固应用·激活·巩固 应用·激活·巩固例2、经过P(3,2)画 直线,使斜率分别为:34 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固(三)应用、激活、巩固 ——小试牛刀,轻松过关应用·激活·巩固 应用·激活·巩固应用·激活·巩固 应用·激活·巩固例2、经过P(3,2) 画直线,使斜率分别为:3-4联想、拓展、引申 联想、拓展、引申(四)联想、拓展、引申 —跳一跳,你能有更大的收获联想、拓展、引申 联想、拓展、引申联想、拓展、引申 联想、拓展、引申 (四)联想、拓展、引申 —跳一跳,你能有更大的收获联想、拓展、引申 联想、拓展、引申反馈·矫正·确认 反馈·矫正·确认五、反馈、矫正、确认—试试你就行,拼拼你能赢。 动动手,你能从中享受到成功的喜悦。反馈·矫正·确认 反馈·矫正·确认练习1、(☆15分)已知点P(2,3),点Q在y轴上,若直线PQ
的斜率为1,则点Q的坐标为_________练习3、 (☆ ☆ 20分)已知三点A(1,1),B(3,5),C(-1,a)在同一
直线上,求a的值。练习2、 (☆15分)斜率为2的直线,经过点(3,5),(a,7),(-1,b)
三点,则a=_____b=________。练习4、 (☆ ☆ 20分)已知直线l过点A(m,2),B(1,m2+2),试
求直线l的斜率。练习5、 (☆ ☆ ☆ 30分)求过P(0,2)和M(2,2m2+12m+10),
m∈R的直线l斜率k的取值范围。2、两种重要数学思想 回顾过去,硕果累累;展望未来,满怀希望! 回顾过去,硕果累累;展望未来,满怀希望! 归纳·总结·提高 归纳·总结·提高 归纳·总结·提高 归纳·总结·提高1、一个斜率公式:(六)归纳总结提高——提升新境界唱好一二三之歌,斜率问题轻松过。 1、数形结合思想:2、类比推理思想:3、三类数学应用:⑴已知直线上两点求斜率;⑵已知一点和斜率画直线;⑶给出三点,判断或证明三点共线。 回顾过去,硕果累累;展望未来,满怀希望! 回顾过去,硕果累累;展望未来,满怀希望!探究、思考、提升 探究、思考、提升 (七)探究、思考、提升——相信自己,你能行探究、思考、提升 探究、思考、提升 作业:P70.练习:1,2,3,4探究与思考1:斜率k与一次函数y=kx+b中的k有何关系?探究与思考2:直线的倾斜程度除了用坡度、斜率来刻画
外,你认为还可以用什么来度量?并进一
步探讨它与斜率之间的关系。
BC的坡度=_________即:坡度=说明:坡度越_____,钢丝越______主动探究是解决问题的金钥匙 主动探究是解决问题的金钥匙 引导·合作·探究 引导·合作·探究 问题3:在平面直角坐标系中,如何用类似的思想方法去刻画直线的倾斜程度呢?如图:已知直线上两点P(x1,y1),
Q(x2,y2),如果x1≠x2,那么刻画直
线的“坡度”是什么呢?y2-y1x2-x1 引导·合作·探究 引导·合作·探究直线斜率的定义:主动探究是解决问题的金钥匙 主动探究是解决问题的金钥匙已知直线上两点P(x1,y1),Q(x2,y2),如果x1≠x2,
则直线PQ的斜率为:形数斜率为0,这时直线PQ平行于x轴或与x轴重合。(2)如果y1=y2,则直线PQ的斜率怎样?(1)如果x1=x2,则直线PQ的斜率怎样? 引导·合作·探究 引导·合作·探究主动探究是解决问题的金钥匙 主动探究是解决问题的金钥匙问题4:研究特例:斜率不存在,这时直线PQ垂直于x轴联想、拓展、引申 联想、拓展、引申问题5:斜率公式的结构如何?下标的次序能否改变?联想、拓展、引申 联想、拓展、引申y2-y1=△yx2-x1=△xy2-y1x2-x1联想、拓展、引申 联想、拓展、引申问题6:联想、拓展、引申 联想、拓展、引申 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固(三)应用、激活、巩固 ——小试牛刀,轻松过关应用·激活·巩固 应用·激活·巩固应用·激活·巩固 应用·激活·巩固例1、如图,直线l1、l2、l3、l4都经过P(3,2),又l1、l2、
l3、l4分别经过A(-1,0)、B(5,-2)、C(-2,2)、D(3,4)。
讨论直线l1、l2、l3、l4的斜率是否存在,若存在,
求出直线的斜率解:设直线l1、l2、l3、l4的斜率分别为k1、k2、k3、k4,则:直线从左下方向右上方倾斜k>0直线从左上方向右下方倾斜k<0联想、拓展、引申 联想、拓展、引申题后反思,联想拓展 —思一思,想一想,你能有更大的进步联想、拓展、引申 联想、拓展、引申问题7:直线的方向与斜率之间有何对应关系?12k=0直线与x轴平行或重合3k不存在直线垂直于x 轴4 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固(三)应用、激活、巩固 ——小试牛刀,轻松过关应用·激活·巩固 应用·激活·巩固应用·激活·巩固 应用·激活·巩固例2、经过P(3,2)画 直线,使斜率分别为:34 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固 应用·激活·巩固(三)应用、激活、巩固 ——小试牛刀,轻松过关应用·激活·巩固 应用·激活·巩固应用·激活·巩固 应用·激活·巩固例2、经过P(3,2) 画直线,使斜率分别为:3-4联想、拓展、引申 联想、拓展、引申(四)联想、拓展、引申 —跳一跳,你能有更大的收获联想、拓展、引申 联想、拓展、引申联想、拓展、引申 联想、拓展、引申 (四)联想、拓展、引申 —跳一跳,你能有更大的收获联想、拓展、引申 联想、拓展、引申反馈·矫正·确认 反馈·矫正·确认五、反馈、矫正、确认—试试你就行,拼拼你能赢。 动动手,你能从中享受到成功的喜悦。反馈·矫正·确认 反馈·矫正·确认练习1、(☆15分)已知点P(2,3),点Q在y轴上,若直线PQ
的斜率为1,则点Q的坐标为_________练习3、 (☆ ☆ 20分)已知三点A(1,1),B(3,5),C(-1,a)在同一
直线上,求a的值。练习2、 (☆15分)斜率为2的直线,经过点(3,5),(a,7),(-1,b)
三点,则a=_____b=________。练习4、 (☆ ☆ 20分)已知直线l过点A(m,2),B(1,m2+2),试
求直线l的斜率。练习5、 (☆ ☆ ☆ 30分)求过P(0,2)和M(2,2m2+12m+10),
m∈R的直线l斜率k的取值范围。2、两种重要数学思想 回顾过去,硕果累累;展望未来,满怀希望! 回顾过去,硕果累累;展望未来,满怀希望! 归纳·总结·提高 归纳·总结·提高 归纳·总结·提高 归纳·总结·提高1、一个斜率公式:(六)归纳总结提高——提升新境界唱好一二三之歌,斜率问题轻松过。 1、数形结合思想:2、类比推理思想:3、三类数学应用:⑴已知直线上两点求斜率;⑵已知一点和斜率画直线;⑶给出三点,判断或证明三点共线。 回顾过去,硕果累累;展望未来,满怀希望! 回顾过去,硕果累累;展望未来,满怀希望!探究、思考、提升 探究、思考、提升 (七)探究、思考、提升——相信自己,你能行探究、思考、提升 探究、思考、提升 作业:P70.练习:1,2,3,4探究与思考1:斜率k与一次函数y=kx+b中的k有何关系?探究与思考2:直线的倾斜程度除了用坡度、斜率来刻画
外,你认为还可以用什么来度量?并进一
步探讨它与斜率之间的关系。
