2018年高中数学第2章平面解析几何初步2.2.1圆的方程课件4苏教版必修2(17张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.2.1圆的方程课件4苏教版必修2(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 235.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览


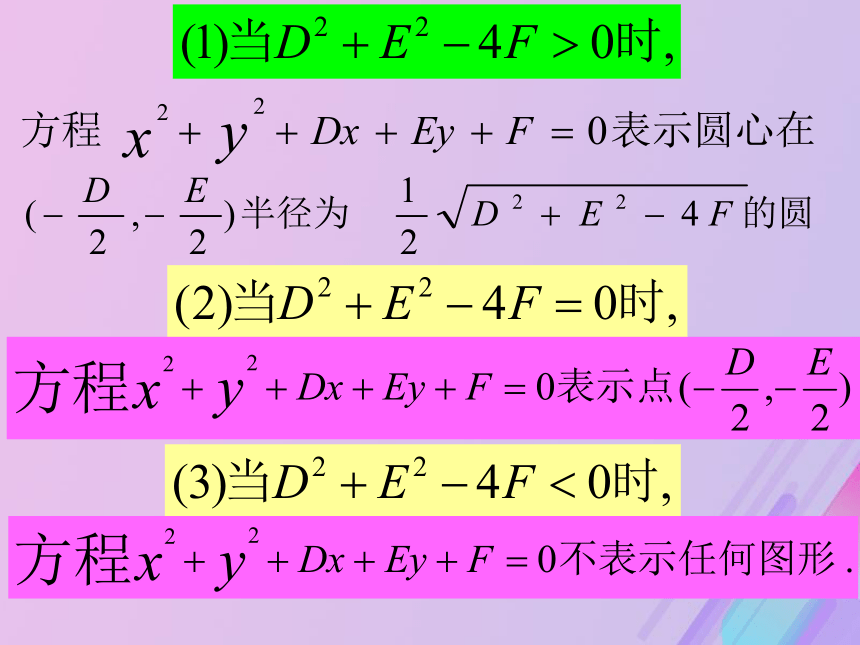




文档简介
课件17张PPT。圆的方程(2)
——一般方程得:x2+y2-2a x-2by+a2+b2-r2=0即:x2+y2+Dx+Ey+F=0讨论:方程:x2+y2+Dx+Ey+F=0表示圆吗?[定义] : 圆的一般方程思
考什么时候可以表示圆?[观察]:圆的标准方程与圆的一般 方程在形式上的异同点.圆的标准方程
圆的一般方程
[说明]:
(1)圆的标准方程的优点在于它明确地指出了圆心和半径 ;
(2)圆的一般方程突出了方程形式上的特点.①是②不是③不是例1: 下列方程各表示什么图形?若是圆则
求出圆心、半径.a例2:巩固:4-6-32或-2(1)圆的一般方程与圆的标准方程的联系:一般方程标准方程[小结一]:例3:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程圆心:两条弦的中垂线的交点半径:圆心到圆上一点xyOEA(5,1)B(7,-3)C(2,-8)几何方法方法一:方法二:待定系数法
待定系数法解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为例3:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程方法三:待定系数法
解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为例3:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程注意:求圆的方程时,要学会根据题目
条件,恰当选择圆的方程形式:①若知道或涉及圆心和半径,我们一般采用
圆的标准方程较简单.②若已知三点求圆的方程,我们常常采用
圆的一般方程用待定系数法求解. [小结二]:(特殊情况时,可借助图象求解更简单)圆心:两条直线的交点半径:圆心到圆上一点xyOCA(1,1)B(2,-2)弦AB的垂直平分线例4.己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的方程.几何方法 例5、如图是某圆拱桥的—孔圆拱的示意图.该圆拱跨度AB=36m,拱高OP=6m,在建造时每隔3m需用一个支柱支撑,求支柱 的长度(精确到0.01m).所在圆的方程是
y=5.39小结(1)当 时,表示圆,(2)当 时,表示点(3)当 时,不表示任何图形2、用待定系数法求圆的方程时,对容易求出圆心坐标的,一般采用圆的标准方程,否则采用一般方程。
3、要画出圆,必须要知道圆心和半径,应会用配方法求圆心和半径,还有公式求圆心和半径。1、小结:求圆的方程几何方法 求圆心坐标 (两条直线的交点)(常用弦的中垂线) 求 半径 (圆心到圆上一点的距离) 写出圆的标准方程待定系数法列关于a,b,r(或D,E,F)的方程组解出a,b,r(或D,E,F),写出标准方程(或一般方程)
——一般方程得:x2+y2-2a x-2by+a2+b2-r2=0即:x2+y2+Dx+Ey+F=0讨论:方程:x2+y2+Dx+Ey+F=0表示圆吗?[定义] : 圆的一般方程思
考什么时候可以表示圆?[观察]:圆的标准方程与圆的一般 方程在形式上的异同点.圆的标准方程
圆的一般方程
[说明]:
(1)圆的标准方程的优点在于它明确地指出了圆心和半径 ;
(2)圆的一般方程突出了方程形式上的特点.①是②不是③不是例1: 下列方程各表示什么图形?若是圆则
求出圆心、半径.a例2:巩固:4-6-32或-2(1)圆的一般方程与圆的标准方程的联系:一般方程标准方程[小结一]:例3:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程圆心:两条弦的中垂线的交点半径:圆心到圆上一点xyOEA(5,1)B(7,-3)C(2,-8)几何方法方法一:方法二:待定系数法
待定系数法解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为例3:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程方法三:待定系数法
解:设所求圆的方程为:因为A(5,1),B (7,-3),C(2,8)都在圆上所求圆的方程为例3:求过三点A(5,1),B (7,-3),C(2,-8)的圆的方程注意:求圆的方程时,要学会根据题目
条件,恰当选择圆的方程形式:①若知道或涉及圆心和半径,我们一般采用
圆的标准方程较简单.②若已知三点求圆的方程,我们常常采用
圆的一般方程用待定系数法求解. [小结二]:(特殊情况时,可借助图象求解更简单)圆心:两条直线的交点半径:圆心到圆上一点xyOCA(1,1)B(2,-2)弦AB的垂直平分线例4.己知圆心为C的圆经过点A(1,1)和B(2,-2),且圆心在直线l:x-y+1=0上,求圆心为C的圆的方程.几何方法 例5、如图是某圆拱桥的—孔圆拱的示意图.该圆拱跨度AB=36m,拱高OP=6m,在建造时每隔3m需用一个支柱支撑,求支柱 的长度(精确到0.01m).所在圆的方程是
y=5.39小结(1)当 时,表示圆,(2)当 时,表示点(3)当 时,不表示任何图形2、用待定系数法求圆的方程时,对容易求出圆心坐标的,一般采用圆的标准方程,否则采用一般方程。
3、要画出圆,必须要知道圆心和半径,应会用配方法求圆心和半径,还有公式求圆心和半径。1、小结:求圆的方程几何方法 求圆心坐标 (两条直线的交点)(常用弦的中垂线) 求 半径 (圆心到圆上一点的距离) 写出圆的标准方程待定系数法列关于a,b,r(或D,E,F)的方程组解出a,b,r(或D,E,F),写出标准方程(或一般方程)
