2018年高中数学第2章平面解析几何初步2.2.2直线与圆的位置关系课件7苏教版必修2(15张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.2.2直线与圆的位置关系课件7苏教版必修2(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 250.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 10:54:39 | ||
图片预览





文档简介
课件15张PPT。2.2.2 直线和圆的位置关系实例引入:一轮红日从海平面上冉冉升起。
请仔细观察图中直线与圆的公共点的个数情况
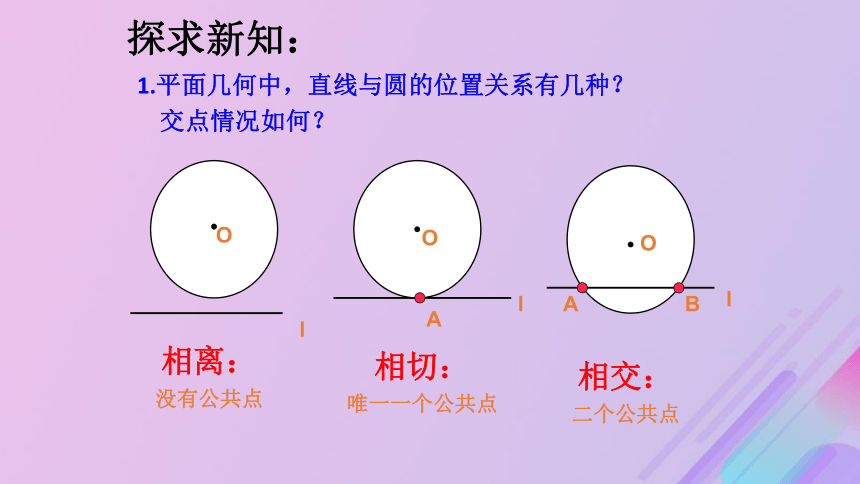
探求新知:1.平面几何中,直线与圆的位置关系有几种?
交点情况如何?相离:
没有公共点相切:
唯一一个公共点相交:
二个公共点 能否利用直线与圆的方程
判断它们之间的位置关系呢?
先看以下问题,看看你能否从问题中总结来.已知直线 与圆 ,
判断它们的位置关系。,方程组有唯一一个解构建新知已知直线 与圆 ,
判断它们的位置关系。已知圆的圆心是O(0,0),半径是r=1,圆心到直线的距离所以,此直线与圆相切构建新知1.代数法:由 消元得一
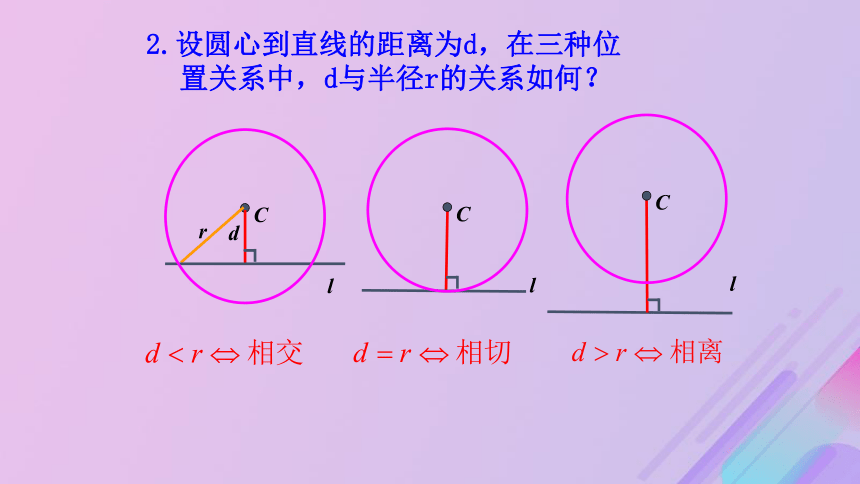
元二次方程的判别式 (1)利用直线与圆的公共点的个数进行判断:
(代数法)(2)利用圆心到直线的距离d与半径r的大小关系判断:(几何法)直线与圆相离直线与圆相切直线与圆相交直线l:Ax+By+C=0圆C:(x-a)2+(y-b)2=r2(r>0)典例精析解:由题意得,圆心C(1,2)
且P(2,3)在圆上即x-y+1=0解:由题意得,圆心C(1,-2)且点P(2,3)在圆外过P点的切线有两条(1)当直线l的斜率存在时,
设直线l的方程为即求过一点P的圆的切线方程问题需注意:1.先判断点P与圆的位置关系2.在求切线的过程中,要注意讨论斜率不存在的情况解:圆心C(3,4)到直线l的距离弦长弦长l与圆心到直线的距离d以及圆的半径r的关系式归纳小结:一.直线与圆位置关系的判断二. 位置关系的应用1.求切线方程问题;2.和弦长有关的问题
请仔细观察图中直线与圆的公共点的个数情况
探求新知:1.平面几何中,直线与圆的位置关系有几种?
交点情况如何?相离:
没有公共点相切:
唯一一个公共点相交:
二个公共点 能否利用直线与圆的方程
判断它们之间的位置关系呢?
先看以下问题,看看你能否从问题中总结来.已知直线 与圆 ,
判断它们的位置关系。,方程组有唯一一个解构建新知已知直线 与圆 ,
判断它们的位置关系。已知圆的圆心是O(0,0),半径是r=1,圆心到直线的距离所以,此直线与圆相切构建新知1.代数法:由 消元得一
元二次方程的判别式 (1)利用直线与圆的公共点的个数进行判断:
(代数法)(2)利用圆心到直线的距离d与半径r的大小关系判断:(几何法)直线与圆相离直线与圆相切直线与圆相交直线l:Ax+By+C=0圆C:(x-a)2+(y-b)2=r2(r>0)典例精析解:由题意得,圆心C(1,2)
且P(2,3)在圆上即x-y+1=0解:由题意得,圆心C(1,-2)且点P(2,3)在圆外过P点的切线有两条(1)当直线l的斜率存在时,
设直线l的方程为即求过一点P的圆的切线方程问题需注意:1.先判断点P与圆的位置关系2.在求切线的过程中,要注意讨论斜率不存在的情况解:圆心C(3,4)到直线l的距离弦长弦长l与圆心到直线的距离d以及圆的半径r的关系式归纳小结:一.直线与圆位置关系的判断二. 位置关系的应用1.求切线方程问题;2.和弦长有关的问题
