2018年高中数学第2章平面解析几何初步2.2.3圆与圆的位置关系课件3苏教版必修2(16张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.2.3圆与圆的位置关系课件3苏教版必修2(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 225.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 10:54:57 | ||
图片预览






文档简介
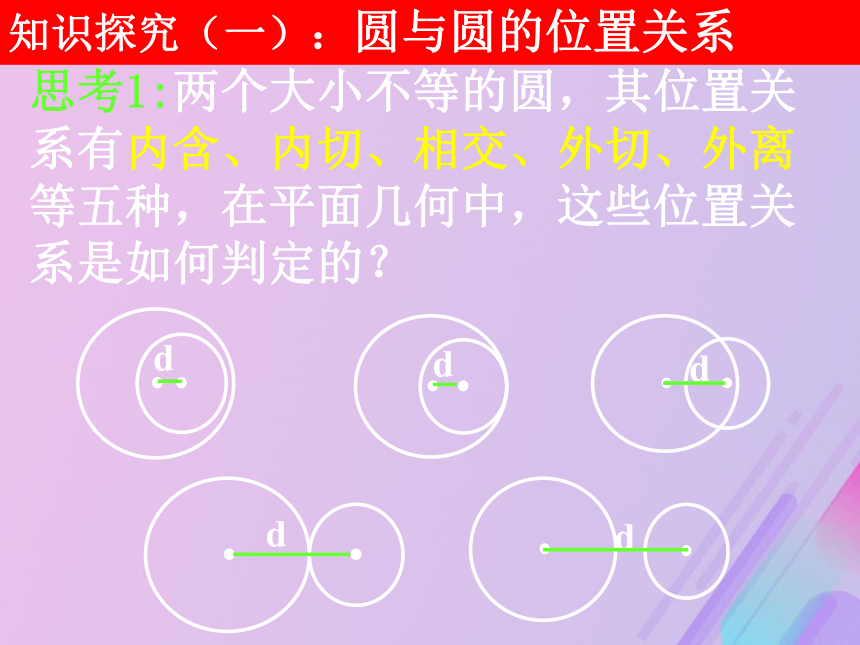
课件16张PPT。圆与圆的位置关系问题提出 1.点与圆、直线与圆的位置关系有哪几种?如何判定这些位置关系?1.点在圆内、点在圆上、点在圆外2.圆与圆的位置关系有哪几种?如何根据圆的方程判断圆与圆的位置关系,我们将进一步探究.
圆与圆的位置关系知识探究(一):圆与圆的位置关系思考1:两个大小不等的圆,其位置关系有内含、内切、相交、外切、外离等五种,在平面几何中,这些位置关系是如何判定的? 思考2:已知两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0,用上述方法判断两个圆位置关系的操作步骤如何? 1.将两圆的方程化为标准方程;2.求两圆的圆心坐标和半径R、r;3.求两圆的圆心距d; 4.比较d与|R-r|,R+r的大小关系:思考3:能否根据两个圆的公共点个数判断两圆的位置关系? 若d<|R-r|,则两圆内含; 若d=|R-r|,则两圆内切; 若|R-r|<d<R+r,则两圆相交;若d=R+r,则两圆外切; 若d>R+r,则两圆外离. 1)两个圆没有公共点,并且每个圆上的点都
在另一个圆的外部时,叫做这两圆外离。2)两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个外切。这个唯一的公共点叫做切点。3)两个圆有两个公共点时,叫做这两个圆相交。4)两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。这个唯一的公共点叫做切点。5)两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含。
两圆同心是两圆内含的一种特例。
小结
外离外切相交内切内含01210d>R+r
d=R+r
|R-r|< d< R+rd=R-rd圆的外部一圆在另一
圆的外部两圆相交一圆在另一
圆的内部一圆在另一
圆的内部名称谢谢知识探究(二):相交圆的交线方程 思考1:已知两圆
C1:x2+y2+D1x+E1y+F1=0和
C2:x2+y2+D2x+E2y+F2=0, 则方程
x2+y2+D1x+E1y+F1-(x2+y2+D2x+E2y+F2)=0表示的图形是什么?思考2:若两圆
C1:x2+y2+D1x+E1y+F1=0 和
C2:x2+y2+D2x+E2y+F2=0相交, M(x0,y0)为一个交点, 则点M(x0,y0)在直线
(D1-D2)x+(E1-E2)y+F1-F2=0上吗? 思考3:若两圆
C1:x2+y2+D1x+E1y+F1=0和
C2:x2+y2+D2x+E2y+F2=0相交, 则其公共弦所在直线的方程是 (D1-D2)x+(E1-E2)y+F1-F2=0,那么过交点的圆系方程是什么? m(x2+y2+D1x+E1y+F1)+n(x2+y2+D2x+E2y+F2)=0 思考4:若两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0相切, 则方程
(D1-D2)x+(E1-E2)y+F1-F2=0表示的直线是什么?若两圆相离呢?理论迁移 例1 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,判断圆C1与圆C2的位置关系. 若相交,求两圆的公共弦所在的直线方程. x2+y2-6x-4=0 x2+y2-4x-2y-1=0 例2 已知一个圆的圆心为M(2,1),且与圆C:x2+y2-3x=0相交于A、B两点,若圆心M到直线AB的距离为 ,求圆M的方程.
圆与圆的位置关系知识探究(一):圆与圆的位置关系思考1:两个大小不等的圆,其位置关系有内含、内切、相交、外切、外离等五种,在平面几何中,这些位置关系是如何判定的? 思考2:已知两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0,用上述方法判断两个圆位置关系的操作步骤如何? 1.将两圆的方程化为标准方程;2.求两圆的圆心坐标和半径R、r;3.求两圆的圆心距d; 4.比较d与|R-r|,R+r的大小关系:思考3:能否根据两个圆的公共点个数判断两圆的位置关系? 若d<|R-r|,则两圆内含; 若d=|R-r|,则两圆内切; 若|R-r|<d<R+r,则两圆相交;若d=R+r,则两圆外切; 若d>R+r,则两圆外离. 1)两个圆没有公共点,并且每个圆上的点都
在另一个圆的外部时,叫做这两圆外离。2)两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外部时,叫做这两个外切。这个唯一的公共点叫做切点。3)两个圆有两个公共点时,叫做这两个圆相交。4)两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。这个唯一的公共点叫做切点。5)两个圆没有公共点,并且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含。
两圆同心是两圆内含的一种特例。
小结
外离外切相交内切内含01210d>R+r
d=R+r
|R-r|< d< R+rd=R-rd
圆的外部两圆相交一圆在另一
圆的内部一圆在另一
圆的内部名称谢谢知识探究(二):相交圆的交线方程 思考1:已知两圆
C1:x2+y2+D1x+E1y+F1=0和
C2:x2+y2+D2x+E2y+F2=0, 则方程
x2+y2+D1x+E1y+F1-(x2+y2+D2x+E2y+F2)=0表示的图形是什么?思考2:若两圆
C1:x2+y2+D1x+E1y+F1=0 和
C2:x2+y2+D2x+E2y+F2=0相交, M(x0,y0)为一个交点, 则点M(x0,y0)在直线
(D1-D2)x+(E1-E2)y+F1-F2=0上吗? 思考3:若两圆
C1:x2+y2+D1x+E1y+F1=0和
C2:x2+y2+D2x+E2y+F2=0相交, 则其公共弦所在直线的方程是 (D1-D2)x+(E1-E2)y+F1-F2=0,那么过交点的圆系方程是什么? m(x2+y2+D1x+E1y+F1)+n(x2+y2+D2x+E2y+F2)=0 思考4:若两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0相切, 则方程
(D1-D2)x+(E1-E2)y+F1-F2=0表示的直线是什么?若两圆相离呢?理论迁移 例1 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,判断圆C1与圆C2的位置关系. 若相交,求两圆的公共弦所在的直线方程. x2+y2-6x-4=0 x2+y2-4x-2y-1=0 例2 已知一个圆的圆心为M(2,1),且与圆C:x2+y2-3x=0相交于A、B两点,若圆心M到直线AB的距离为 ,求圆M的方程.
