2018年高中数学第1章立体几何初步1.1.1棱柱、棱锥和棱台课件5苏教版必修2(27张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.1.1棱柱、棱锥和棱台课件5苏教版必修2(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览


文档简介
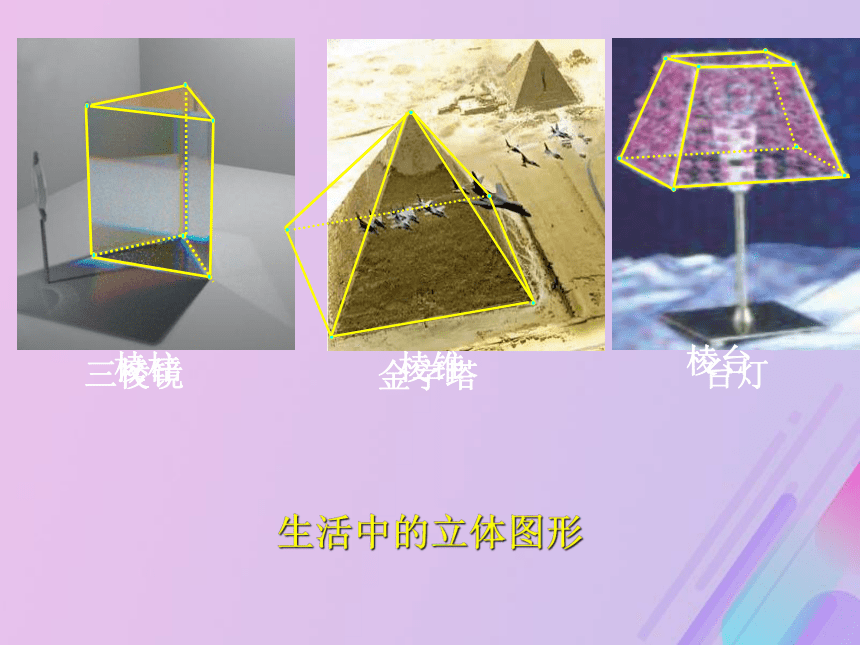
课件27张PPT。立体几何初步棱柱、棱锥、棱台生活中的数学:生活中的立体图形三棱镜金字塔台灯棱柱棱锥棱台(1)一个点按某一确定的方向移动一定
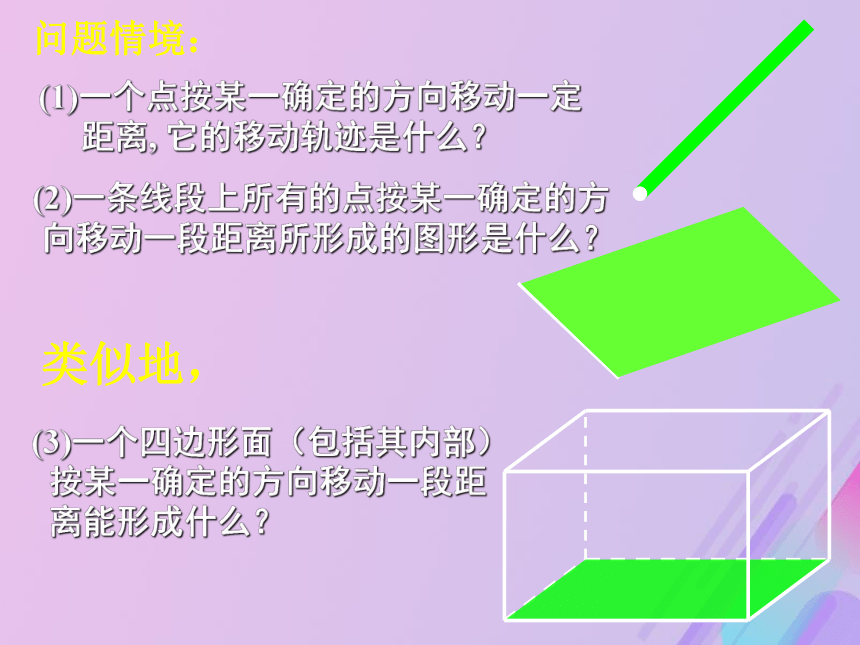
距离, 它的移动轨迹是什么?(2)一条线段上所有的点按某一确定的方
向移动一段距离所形成的图形是什么?问题情境:类似地,(3)一个四边形面(包括其内部)
按某一确定的方向移动一段距
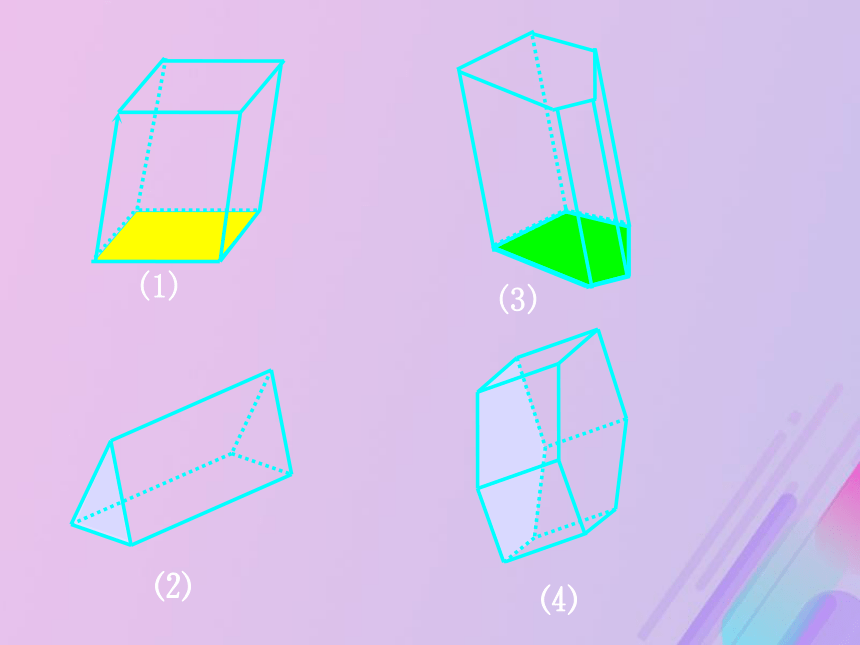
离能形成什么?问题1 仔细观察下面的几何体,想一想我们可以
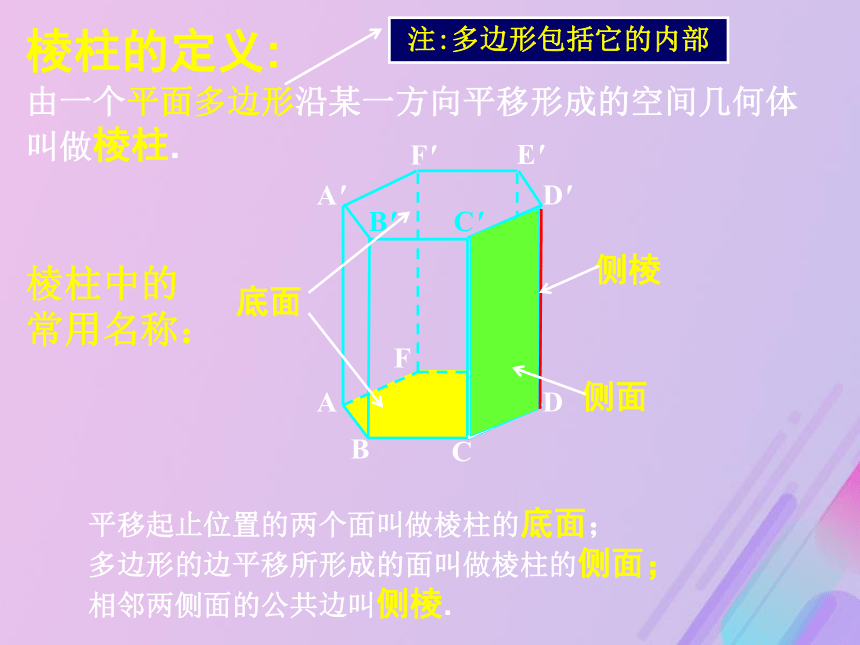
怎样得到这些几何体?4()3()2()1()(1)(3)⑵⑷棱柱的定义:由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.注:多边形包括它的内部平移起止位置的两个面叫做棱柱的底面;
多边形的边平移所形成的面叫做棱柱的侧面;
相邻两侧面的公共边叫侧棱.棱柱中的
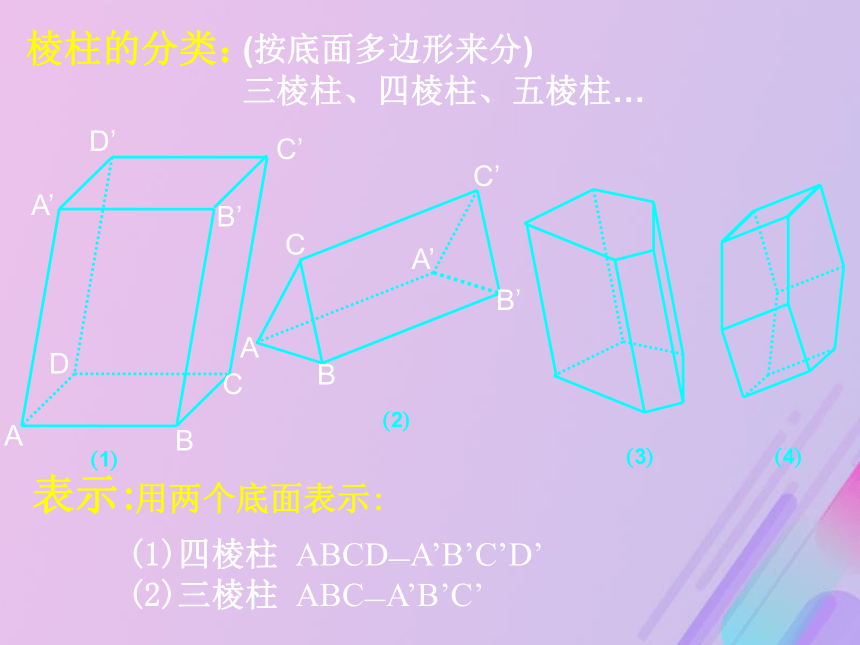
常用名称:ABCDEFA'D'E'F'底面B'C'(按底面多边形来分)
三棱柱、四棱柱、五棱柱… 4()3()2()1()(1)四棱柱 ABCD—A’B’C’D’
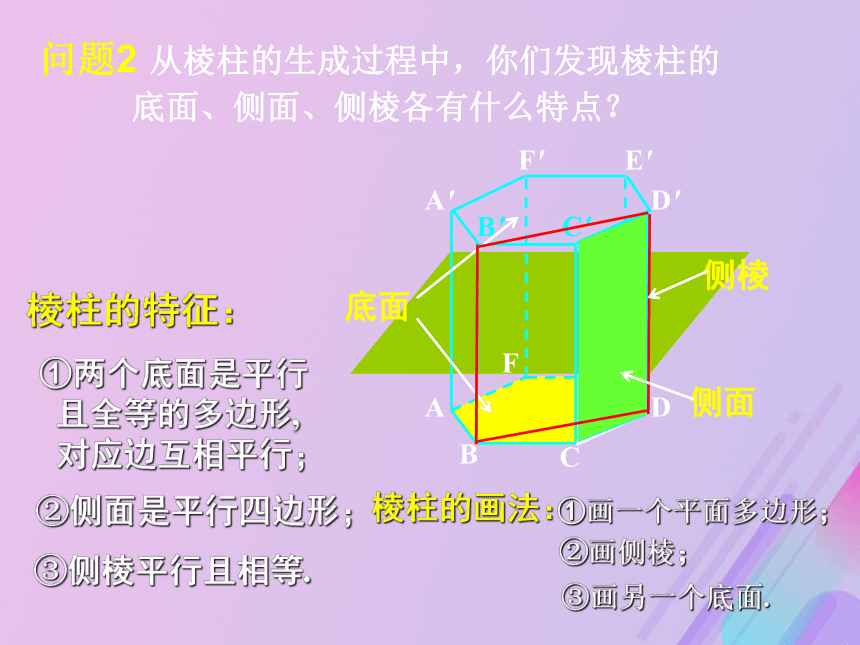
(2)三棱柱 ABC—A’B’C’表示:用两个底面表示:棱柱的分类:问题2 从棱柱的生成过程中,你们发现棱柱的
底面、侧面、侧棱各有什么特点? ①两个底面是平行
且全等的多边形,
对应边互相平行;③侧棱平行且相等.②侧面是平行四边形;棱柱的特征:ABCDEFA'D'E'F'底面B'C'棱柱的画法:①画一个平面多边形;②画侧棱;③画另一个底面.练习1:下面的几何体是棱柱吗?棱柱的概念辨析√√√有两个面平行,其余各面都是平行四边形的几何体是棱柱吗?棱柱的概念辨析×问题3 观察上下两组几何体,它们的相同点?不同点?用运动变化观点看, 下面的几何体有怎样的变化?ABCDA’B’C’底面DCBAS底面侧面侧棱:相邻侧面的
公共边顶点:由棱柱的一个
底面收缩而成棱锥如何分类?D’棱锥的定义: 当棱柱的一个底面收缩为一个点时,
得到的几何体叫做棱锥。如:四棱锥 S-ABCD用顶点和底面表示:如何表示?类比问题4 从棱锥的生成过程中, 你们发现棱锥有什么特点? ①底面是多边形;③侧棱交于一点.②侧面是共顶点的三角形;棱锥的特征:棱锥的画法:①画一个平面多边形;②画顶点,连线得侧棱.棱锥的概念辨析练习2:下面的几何体是棱锥吗?A①②③FEDCBCBAED三棱锥 A-BCD三棱锥 B-ACD三棱锥 C-ABD三棱锥 D-ABC问题5 用平行于底面的平面去截棱锥,
能得到什么几何体呢? 棱锥被平行于底面的一个平面所截后,截面和底面之间的部分叫做棱台. ACDABCACDEBB问题5 用平行于底面的平面去截棱锥,
能得到什么几何体呢? ACDB 棱锥被平行于底面的一个平面所截后,截面和底面间的部分叫做棱台. 类比 研究棱柱、棱锥的思路,
我们来研究棱台的相关知识。底面侧面侧棱①两个底面是平行
且相似的多边形,
对应边互相平行;③侧棱延长交于一点.②侧面是梯形;棱台的特征:棱台的画法:①画一个棱锥;②画截面;③擦去多余的线.例1.请你画一个四棱柱和一个三棱台;空间图形中的被遮挡的线要画成虚线.棱柱、棱锥与棱台的转化棱柱棱锥棱台分割补形底面缩为点ACBA1A1CB截面A1BC将三棱台分成了两部分,
问:这两部分分别是什么几何体?多面体的定义:
由若干个平面多边形围成的几何体叫做多面体.数学应用1. 想一想你生活中所见到的棱柱、棱锥、棱台的实例。2、请说出下列各个物体是由什么样的棱柱、棱锥、
棱台组成的?数学应用思考题: 请设计一个平面图形,将其适当折叠后可以得到
一个每个面都是正三角形的三棱锥。课堂小结1、棱柱、棱锥、棱台的概念、分类、表示、特性、画法2、用运动变化的观点来认识棱柱、棱锥、棱台的关系我学到了:我该注意的问题是:1、画图时被遮挡住的部分要用虚线表示2、棱台的侧棱延长后应交于一点课外作业:操作与探究1、请你用纸板折叠(或剪拼)成下列几何体的模型:
(1) 三棱柱; (2) 三棱锥; (3) 三棱台。2、我们把平面图形平移运动得到了棱柱,再收缩与分割
得到了棱锥和棱台,还有什么运动方式可以得到新的
空间几何体?谢谢大家!再见!
距离, 它的移动轨迹是什么?(2)一条线段上所有的点按某一确定的方
向移动一段距离所形成的图形是什么?问题情境:类似地,(3)一个四边形面(包括其内部)
按某一确定的方向移动一段距
离能形成什么?问题1 仔细观察下面的几何体,想一想我们可以
怎样得到这些几何体?4()3()2()1()(1)(3)⑵⑷棱柱的定义:由一个平面多边形沿某一方向平移形成的空间几何体叫做棱柱.注:多边形包括它的内部平移起止位置的两个面叫做棱柱的底面;
多边形的边平移所形成的面叫做棱柱的侧面;
相邻两侧面的公共边叫侧棱.棱柱中的
常用名称:ABCDEFA'D'E'F'底面B'C'(按底面多边形来分)
三棱柱、四棱柱、五棱柱… 4()3()2()1()(1)四棱柱 ABCD—A’B’C’D’
(2)三棱柱 ABC—A’B’C’表示:用两个底面表示:棱柱的分类:问题2 从棱柱的生成过程中,你们发现棱柱的
底面、侧面、侧棱各有什么特点? ①两个底面是平行
且全等的多边形,
对应边互相平行;③侧棱平行且相等.②侧面是平行四边形;棱柱的特征:ABCDEFA'D'E'F'底面B'C'棱柱的画法:①画一个平面多边形;②画侧棱;③画另一个底面.练习1:下面的几何体是棱柱吗?棱柱的概念辨析√√√有两个面平行,其余各面都是平行四边形的几何体是棱柱吗?棱柱的概念辨析×问题3 观察上下两组几何体,它们的相同点?不同点?用运动变化观点看, 下面的几何体有怎样的变化?ABCDA’B’C’底面DCBAS底面侧面侧棱:相邻侧面的
公共边顶点:由棱柱的一个
底面收缩而成棱锥如何分类?D’棱锥的定义: 当棱柱的一个底面收缩为一个点时,
得到的几何体叫做棱锥。如:四棱锥 S-ABCD用顶点和底面表示:如何表示?类比问题4 从棱锥的生成过程中, 你们发现棱锥有什么特点? ①底面是多边形;③侧棱交于一点.②侧面是共顶点的三角形;棱锥的特征:棱锥的画法:①画一个平面多边形;②画顶点,连线得侧棱.棱锥的概念辨析练习2:下面的几何体是棱锥吗?A①②③FEDCBCBAED三棱锥 A-BCD三棱锥 B-ACD三棱锥 C-ABD三棱锥 D-ABC问题5 用平行于底面的平面去截棱锥,
能得到什么几何体呢? 棱锥被平行于底面的一个平面所截后,截面和底面之间的部分叫做棱台. ACDABCACDEBB问题5 用平行于底面的平面去截棱锥,
能得到什么几何体呢? ACDB 棱锥被平行于底面的一个平面所截后,截面和底面间的部分叫做棱台. 类比 研究棱柱、棱锥的思路,
我们来研究棱台的相关知识。底面侧面侧棱①两个底面是平行
且相似的多边形,
对应边互相平行;③侧棱延长交于一点.②侧面是梯形;棱台的特征:棱台的画法:①画一个棱锥;②画截面;③擦去多余的线.例1.请你画一个四棱柱和一个三棱台;空间图形中的被遮挡的线要画成虚线.棱柱、棱锥与棱台的转化棱柱棱锥棱台分割补形底面缩为点ACBA1A1CB截面A1BC将三棱台分成了两部分,
问:这两部分分别是什么几何体?多面体的定义:
由若干个平面多边形围成的几何体叫做多面体.数学应用1. 想一想你生活中所见到的棱柱、棱锥、棱台的实例。2、请说出下列各个物体是由什么样的棱柱、棱锥、
棱台组成的?数学应用思考题: 请设计一个平面图形,将其适当折叠后可以得到
一个每个面都是正三角形的三棱锥。课堂小结1、棱柱、棱锥、棱台的概念、分类、表示、特性、画法2、用运动变化的观点来认识棱柱、棱锥、棱台的关系我学到了:我该注意的问题是:1、画图时被遮挡住的部分要用虚线表示2、棱台的侧棱延长后应交于一点课外作业:操作与探究1、请你用纸板折叠(或剪拼)成下列几何体的模型:
(1) 三棱柱; (2) 三棱锥; (3) 三棱台。2、我们把平面图形平移运动得到了棱柱,再收缩与分割
得到了棱锥和棱台,还有什么运动方式可以得到新的
空间几何体?谢谢大家!再见!
