2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件6苏教版必修2(20张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件6苏教版必修2(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览







文档简介
课件20张PPT。 如果代数与几何各自分开发展,那么它的进步将十分缓慢,而且应用范围也很有限。但若两者互相结合而共同发展,则就会相互加强,并以快速的步伐向着完美化的方向猛进。
——拉格朗日完美的流线造型北京奥运场馆如何建造曲线优美的现代化立交桥雨后的彩虹,
完美的曲线平面解析几何的本质以代数的方法研究图形的
几何性质平面直角坐标系解析几何学的创立者法国数学家(1596-1650)2.1.1直线的斜率学习目标:
(1)理解直线的斜率和倾斜角的概念;
(2)了解直线的斜率公式的推导过程,会应用斜率公式求直线的斜率。直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线情境(1)两点确定一条直线,过一点可以
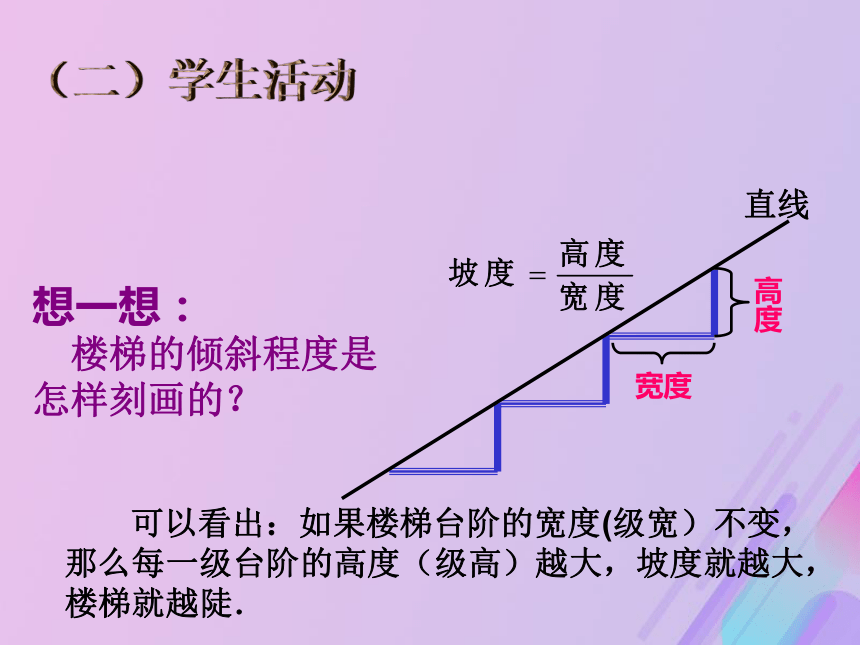
画无数条直线。问题(2)我们熟悉的坡度是怎样确定的?(一)问题情境情境(2)楼梯或路面的倾斜程度可用坡度来刻画。问题(1)过一点要画出一条确定的直线还需什么条件?直线高度宽度想一想:
楼梯的倾斜程度是
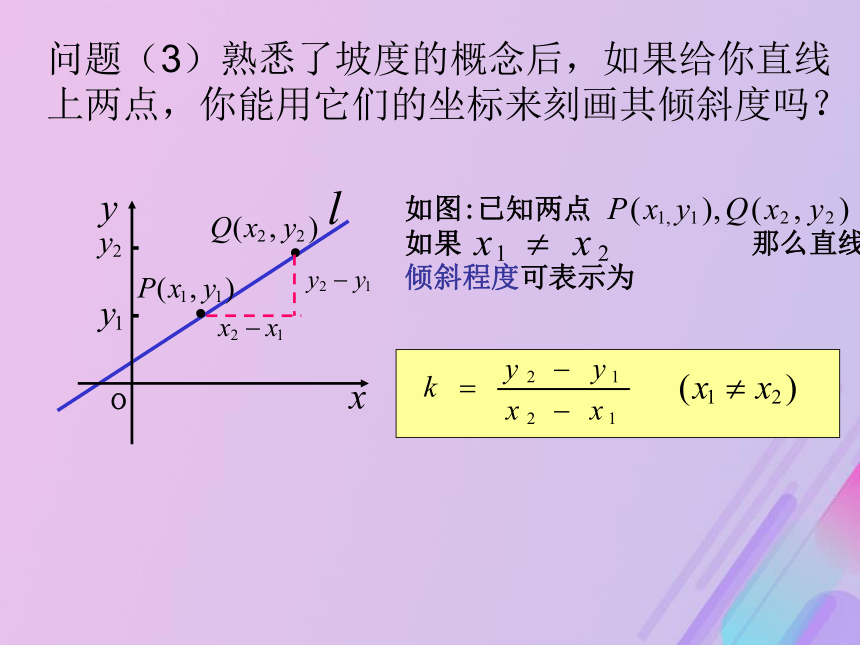
怎样刻画的? 可以看出:如果楼梯台阶的宽度(级宽)不变,那么每一级台阶的高度(级高)越大,坡度就越大,楼梯就越陡.(二)学生活动问题(3)熟悉了坡度的概念后,如果给你直线
上两点,你能用它们的坐标来刻画其倾斜度吗? 已知两点 P(x1,y1), Q(x2,y2), x1≠x2,如图 则直线 PQ的斜率为:
(三)建构数学(1)直线的斜率:(1)斜率公式与两点的顺序有关吗?
(2)对一条与x轴不垂直的定直线而言,直线
的斜率是定值吗?
(3)如果 ,那么直线PQ的斜率怎样?思考:CE(x1,,y1)(x2,,y2)如果K存在,则直线上任意两点确定的K的值总是相等的,是一个定值。当x1=x2时,即直线与x轴垂直时,K不存在。师生互动问题讨论既然垂直于x轴的直线,斜率不存在,我们用
什么来反映这类直线的倾斜程度呢? 同学们可以观察一下图像,讨论后作答。(2)倾斜角的概念:根据定义结合图像说说倾斜角的范围:概括:倾斜角和斜率都是刻画直线倾斜程
度的量,斜率侧重于数量关系,而倾斜角
则更加直观形象. (四)数学应用例1直线 都经过P(3,2),又 分别
经过点 讨论斜率的是否
存在,如存在,求出直线的斜率。直线 的斜率不存在。合作探究: 你能从例1中看到直线的倾斜方向与直线
的斜率有什么联系? (4).当斜率不存在时,直线与x
轴垂直( ) 分析: 要画出直线,只需再确定直线上
另一个点的位置.例2经过点A(3,2)画直线,使直线的斜率
分别为① ;② ;③不存在;④05-4想一想:还有其他的作法吗?为什么?斜率不存在时,直线过
点P并垂直于X轴斜率为0时,直线过点P并平行于X轴提示:待定系数法(五)回顾小结1.直线的斜率的概念及过两点的直线斜
率的计算公式;
2.直线的倾斜角的概念及倾斜角的范围.(六)课后作业书后练习题1、2、3、4.
——拉格朗日完美的流线造型北京奥运场馆如何建造曲线优美的现代化立交桥雨后的彩虹,
完美的曲线平面解析几何的本质以代数的方法研究图形的
几何性质平面直角坐标系解析几何学的创立者法国数学家(1596-1650)2.1.1直线的斜率学习目标:
(1)理解直线的斜率和倾斜角的概念;
(2)了解直线的斜率公式的推导过程,会应用斜率公式求直线的斜率。直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线情境(1)两点确定一条直线,过一点可以
画无数条直线。问题(2)我们熟悉的坡度是怎样确定的?(一)问题情境情境(2)楼梯或路面的倾斜程度可用坡度来刻画。问题(1)过一点要画出一条确定的直线还需什么条件?直线高度宽度想一想:
楼梯的倾斜程度是
怎样刻画的? 可以看出:如果楼梯台阶的宽度(级宽)不变,那么每一级台阶的高度(级高)越大,坡度就越大,楼梯就越陡.(二)学生活动问题(3)熟悉了坡度的概念后,如果给你直线
上两点,你能用它们的坐标来刻画其倾斜度吗? 已知两点 P(x1,y1), Q(x2,y2), x1≠x2,如图 则直线 PQ的斜率为:
(三)建构数学(1)直线的斜率:(1)斜率公式与两点的顺序有关吗?
(2)对一条与x轴不垂直的定直线而言,直线
的斜率是定值吗?
(3)如果 ,那么直线PQ的斜率怎样?思考:CE(x1,,y1)(x2,,y2)如果K存在,则直线上任意两点确定的K的值总是相等的,是一个定值。当x1=x2时,即直线与x轴垂直时,K不存在。师生互动问题讨论既然垂直于x轴的直线,斜率不存在,我们用
什么来反映这类直线的倾斜程度呢? 同学们可以观察一下图像,讨论后作答。(2)倾斜角的概念:根据定义结合图像说说倾斜角的范围:概括:倾斜角和斜率都是刻画直线倾斜程
度的量,斜率侧重于数量关系,而倾斜角
则更加直观形象. (四)数学应用例1直线 都经过P(3,2),又 分别
经过点 讨论斜率的是否
存在,如存在,求出直线的斜率。直线 的斜率不存在。合作探究: 你能从例1中看到直线的倾斜方向与直线
的斜率有什么联系? (4).当斜率不存在时,直线与x
轴垂直( ) 分析: 要画出直线,只需再确定直线上
另一个点的位置.例2经过点A(3,2)画直线,使直线的斜率
分别为① ;② ;③不存在;④05-4想一想:还有其他的作法吗?为什么?斜率不存在时,直线过
点P并垂直于X轴斜率为0时,直线过点P并平行于X轴提示:待定系数法(五)回顾小结1.直线的斜率的概念及过两点的直线斜
率的计算公式;
2.直线的倾斜角的概念及倾斜角的范围.(六)课后作业书后练习题1、2、3、4.
