2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(18张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 224.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:08:19 | ||
图片预览






文档简介
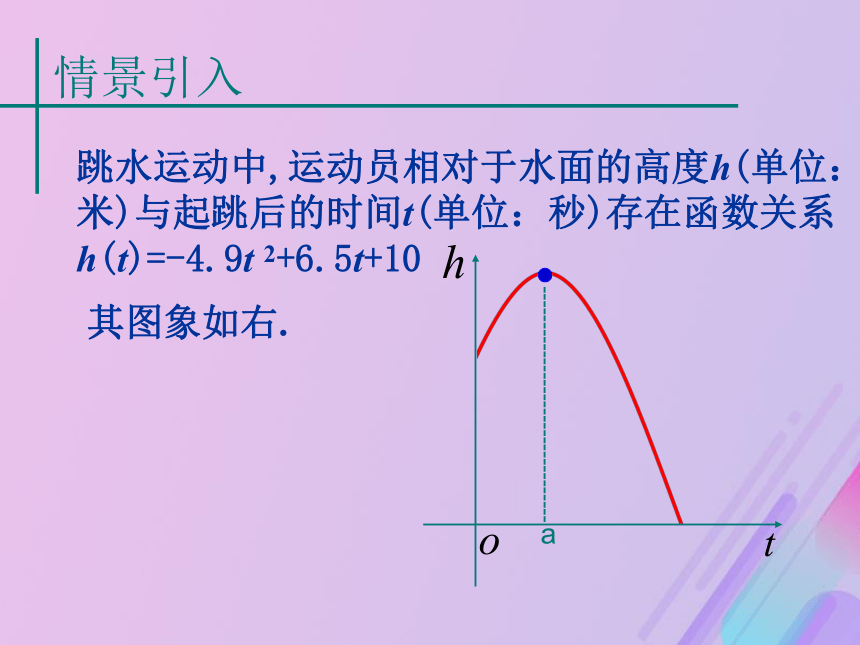
课件18张PPT。函数的极值与导数第三章 导数及其应用跳水运动中,运动员相对于水面的高度h(单位:米)与起跳后的时间t(单位:秒)存在函数关系
h(t)=-4.9t 2+6.5t+10其图象如右.---------------------------------a这就是本课要学习的内容:函数的极值与导数。1、理解极大值、极小值的概念。
2、能够运用判断极大值、极小值的方法求函数的极值。
3、掌握求可导函数的极值的步骤。重点:
1、了解函数在某点处取得极值的必要条件和充分条件。
2、会用导数求不超过三次的多项式函数的极大值和
极小值。
难点:
会用导数求不超过三次的多项式函数的极大值和极小值。
2、你能尝试概括出函数的极大值和极小值的
定义吗?
极值的概念:
函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函
数值都小,f′(a)=0,而且在点x=a附近的左侧f′(x)<0 ,右侧
f′(x)>0 .我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;
类似地,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0,而且在点x=b附近的左侧f′(x)>0 ,右侧f′(x)<0 .把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
极大值点、极小值点统称为极值点,极大值和极小值统称为极值。4、导数值为0的点一定是函数的极值点吗?导数值为0是函数在这点取极值的什么条件? (举例回答)但x=0不是函数的极值点导数为零的点是该点为极值点
的必要条件,而不是充分条件.可导函数在极值点处的导数值为0,
但导数值为0的点不一定是函数的极值点。5、你能通过例4归纳出求函数极值的步骤吗?
(例4后书面总结) 。
,:↗ ↘ 判断极值是极小值或极大值的方法是:3.方法归纳:求函数极值的步骤:当堂达标2.求函数 f(x)=3x-x3的极值。1、函数f(x)的定义域为R,导函数f′(x)的图象如图
所示,则函数f(x)( )
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点解:因为f(x)= 3x-x3,所以f′ (x)=3-3x2令f′ (x)=0,则x=-1或x=1↗ 参考答案:(2). f(x)=3x-x3当x=-1时,函数有极小值,极小值为-2。当x=1时,函数有极大值,极大值为2;(1). C总结·感悟1、了解导数值为0是函数在这点取得极值的必要条件,而非充分条件。
2、理解极大值、极小值的概念及判断方法。
3、掌握求可导函数的极值的步骤。本课结束
h(t)=-4.9t 2+6.5t+10其图象如右.---------------------------------a这就是本课要学习的内容:函数的极值与导数。1、理解极大值、极小值的概念。
2、能够运用判断极大值、极小值的方法求函数的极值。
3、掌握求可导函数的极值的步骤。重点:
1、了解函数在某点处取得极值的必要条件和充分条件。
2、会用导数求不超过三次的多项式函数的极大值和
极小值。
难点:
会用导数求不超过三次的多项式函数的极大值和极小值。
2、你能尝试概括出函数的极大值和极小值的
定义吗?
极值的概念:
函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函
数值都小,f′(a)=0,而且在点x=a附近的左侧f′(x)<0 ,右侧
f′(x)>0 .我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值;
类似地,函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0,而且在点x=b附近的左侧f′(x)>0 ,右侧f′(x)<0 .把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.
极大值点、极小值点统称为极值点,极大值和极小值统称为极值。4、导数值为0的点一定是函数的极值点吗?导数值为0是函数在这点取极值的什么条件? (举例回答)但x=0不是函数的极值点导数为零的点是该点为极值点
的必要条件,而不是充分条件.可导函数在极值点处的导数值为0,
但导数值为0的点不一定是函数的极值点。5、你能通过例4归纳出求函数极值的步骤吗?
(例4后书面总结) 。
,:↗ ↘ 判断极值是极小值或极大值的方法是:3.方法归纳:求函数极值的步骤:当堂达标2.求函数 f(x)=3x-x3的极值。1、函数f(x)的定义域为R,导函数f′(x)的图象如图
所示,则函数f(x)( )
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点解:因为f(x)= 3x-x3,所以f′ (x)=3-3x2令f′ (x)=0,则x=-1或x=1↗ 参考答案:(2). f(x)=3x-x3当x=-1时,函数有极小值,极小值为-2。当x=1时,函数有极大值,极大值为2;(1). C总结·感悟1、了解导数值为0是函数在这点取得极值的必要条件,而非充分条件。
2、理解极大值、极小值的概念及判断方法。
3、掌握求可导函数的极值的步骤。本课结束
