2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.3.2命题的四种形式课件(36张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第一章常用逻辑用语1.3.2命题的四种形式课件(36张) |  | |
| 格式 | zip | ||
| 文件大小 | 381.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:08:52 | ||
图片预览










文档简介
课件36张PPT。1.1.2
四种命题【自主预习】
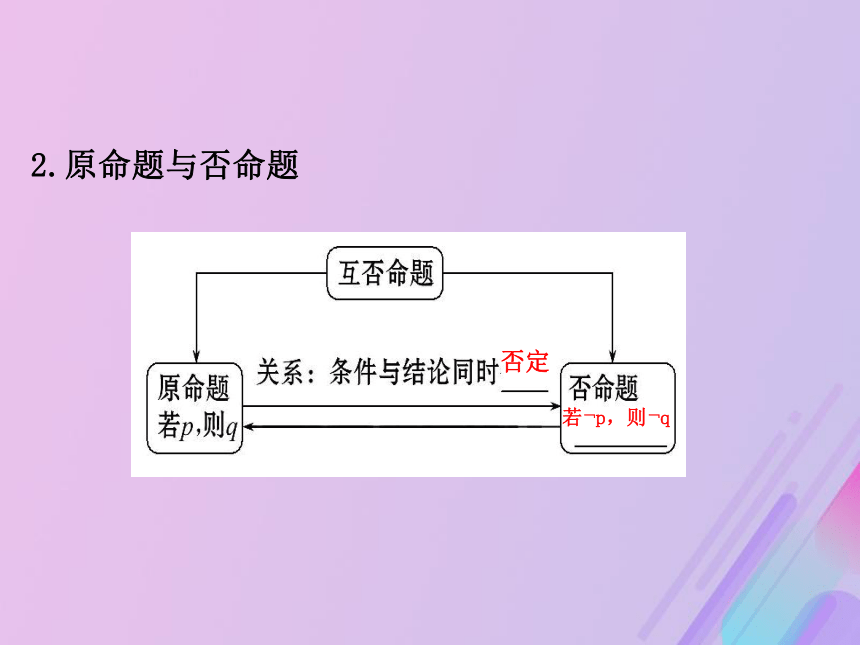
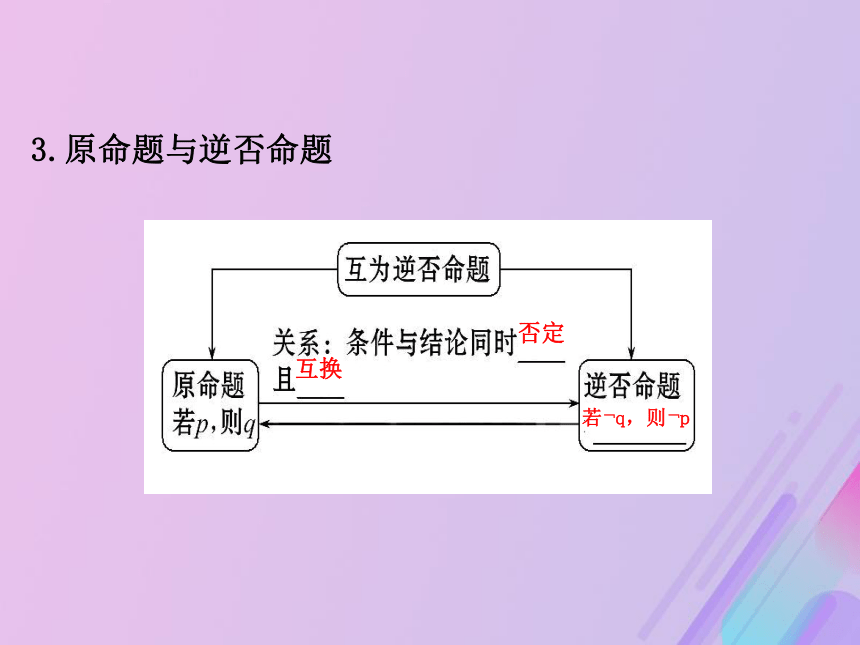
1.原命题与逆命题条件结论若q,则p2.原命题与否命题否定若﹁p,则﹁q3.原命题与逆否命题若﹁q,则﹁p否定互换【即时小测】
1.“若x2=1,则x=1”的否命题为 ( )
A.若x2≠1,则x=1 B.若x2=1,则x≠1
C.若x2≠1,则x≠1 D.若x≠1,则x2≠1
【解析】选C.否命题是对原命题的条件和结论分别否定,所以其否命题为“若x2≠1,则x≠1”.2.已知命题p:“若x≥a2+b2,则x≥2ab”,则下列说法正确的是 ( )
A.命题p的逆命题是“若xB.命题p的逆命题是“若x<2ab,则xC.命题p的否命题是“若xD.命题p的否命题是“若x≥a2+b2,则x<2ab”【解析】选C.命题p的逆命题是“若x≥2ab,则x≥a2+b2”,故A,B都错,命题p的否命题是:“若x探究点 四种命题的概念
1.四种命题中原命题是否是固定的?
提示:原命题不是固定的,任何一个命题都可以作为原命题,从而有另外的三种命题.2.由原命题写出逆命题、否命题、逆否命题的关键是什么?
提示:关键是分清楚原命题的条件和结论,然后按照逆命题、否命题、逆否命题的定义来写.【归纳总结】
四种命题的三个关注点
(1)写原命题的逆命题时,不要交换命题的前提条件.
(2)写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.(3)任何一个命题都包含条件和结论两部分,通过条件和结论的不同变换都可以得到这个命题的逆命题、否命题和逆否命题.因此任何一个命题都有逆命题、否命题和逆否命题.
易错警示:对条件或结论进行否定时易出现错误.如“大于”的否定应是“不大于,即≤”;“都是”的否定为“不都是”等.类型一 四种命题的概念
【典例】1.(2015·山东高考)设m∈R,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是 ( )
A.若方程x2+x-m=0有实根,则m>0
B.若方程x2+x-m=0有实根,则m≤0
C.若方程x2+x-m=0没有实根,则m>0
D.若方程x2+x-m=0没有实根,则m≤02.若命题p的逆命题是q,q的逆否命题是r,则命题r是命题p的 ( )
A.逆命题 B.否命题
C.逆否命题 D.无法确定【解题探究】
1.一个命题的逆否命题的条件和结论与原命题有什么关系?
提示:把原命题的条件和结论否定后再交换位置.
2.判断四种命题间关系的关键是什么?
提示:各个命题的条件和结论.【解析】1.选D.一个命题的逆否命题是将原命题的条件、结论加以否定,并且加以互换.
2.选B.设命题p为“若a,则b”,由题意得:
命题q:若b,则a
命题r:若?a,则?b
所以命题r是命题p的否命题.【延伸探究】
本例1中命题的逆命题和否命题是什么?
【解析】逆命题:若方程x2+x-m=0有实根,则m>0;
否命题:若m≤0,则方程x2+x-m=0没有实根.【方法技巧】四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.【拓展延伸】常见词语的否定【变式训练】1.命题“若α= ,则tanα=1”的逆否命题是 ( )
A.若α≠ ,则tanα=1
B.若α= ,则tanα≠1
C.若tanα≠1,则α≠
D.若tanα≠1,则α=【解析】选C.交换原命题的条件和结论并同时否定,即得原命题的逆否命题,所以应选C.2.设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是 ( )
A.若a≠-b,则|a|≠|b| B.若a=-b,则|a|≠|b|
C.若|a|≠|b|,则a≠-b D.若|a|=|b|,则a=-b
【解析】选D.交换原命题的条件和结论可以得到原命题的逆命题.类型二 四种命题真假的判断
【典例】1.有下列命题:①“若x2+y2=0,则x,y全是0”的否命题;②“全等三角形是相似三角形”的否命题;③“若m≥1,则mx2-2(m+1)x+m+3>0的解集是R”的逆命题;④“若a+7是无理数,则a是无理数”的逆否命题.其中为真命题的是 ( )
A.①②③ B.②③④ C.①③④ D.①④2.已知命题“若m-1【解题探究】
1.典例1①中如何否定“x,y全是0”?
提示:x,y不全是0.
2.典例2中逆命题为真的含义是什么?
提示:可以由1②否命题为“不全等的三角形不相似”,为假.
③逆命题为“若mx2-2(m+1)x+m+3>0的解集为“R”,则m≥1”.
因为当m=0时,解集不是R,所以应有 即m>1.
所以其逆命题是假命题.④逆否命题为“若a不是无理数,则a+7不是无理数”,显然当a是有理数时,a+7也是有理数,故逆否命题为真.
2.由已知得,若1 所以1≤m≤2.
答案:[1,2]【延伸探究】
本例2中的否命题是什么?
【解析】否命题为:若x≤m-1或x≥m+1,则x≤1或x≥2.【方法技巧】判断四种命题真假的方法
(1)要正确理解四种命题间的相互关系.
(2)正确利用相关知识进行判断推理.
(3)若由p经逻辑推理得出q,则命题“若p,则q”为真;确定“若p,则q”为假时,则只需举一个反例说明即可.【变式训练】命题“若a>b,则ac2>bc2(a,b,c∈R)”与
它的逆命题、否命题、逆否命题中,真命题的个数为
( )
A.0 B.2 C.3 D.4【解析】选B.原命题“若a>b,则ac2>bc2(a,b,c∈R)”为假命题;逆命题“若ac2>bc2,则a>b(a,b,c∈R)”为真命题;否命题“若a≤b,则ac2≤bc2(a,b,c∈R)”为真命题;逆否命题“若ac2≤bc2,则a≤b(a,b,c∈R)”为假命题.【补偿训练】(2016·海淀高二检测)命题“如果直线l垂直于平面α内的两条相交直线,则直线l垂直于平面α”的否命题是________;该否命题是________(填“真”或“假”)命题. 【解析】命题“如果直线l垂直于平面α内的两条相交直线,则直线l垂直于平面α”的否命题是:如果直线l不垂直于平面α内的两条相交直线,则直线l不垂直于平面α;
直线与平面垂直的充要条件是直线与平面内的所有直线都垂直,所以命题的否命题是真命题.答案:如果直线l不垂直于平面α内的两条相交直线,则直线l不垂直于平面α 真自我纠错 逆否命题的改写
【典例】(2016·荆州高二检测)命题:“a,b都是奇数,
则a+b是偶数”的逆否命题是_____________________,
是____(填“真”或“假”)命题.【失误案例】分析解题过程,找出错误之处,并写出正确答案.
提示:错误的根本原因是否定“都是”时出现错误,从而导致真假性判断错误,“都是”应否定为“不都是”.【解析】逆否命题:若a+b不是偶数,则a,b不都是奇数.是真命题.
答案:若a+b不是偶数,则a,b不都是奇数 真
四种命题【自主预习】
1.原命题与逆命题条件结论若q,则p2.原命题与否命题否定若﹁p,则﹁q3.原命题与逆否命题若﹁q,则﹁p否定互换【即时小测】
1.“若x2=1,则x=1”的否命题为 ( )
A.若x2≠1,则x=1 B.若x2=1,则x≠1
C.若x2≠1,则x≠1 D.若x≠1,则x2≠1
【解析】选C.否命题是对原命题的条件和结论分别否定,所以其否命题为“若x2≠1,则x≠1”.2.已知命题p:“若x≥a2+b2,则x≥2ab”,则下列说法正确的是 ( )
A.命题p的逆命题是“若x
1.四种命题中原命题是否是固定的?
提示:原命题不是固定的,任何一个命题都可以作为原命题,从而有另外的三种命题.2.由原命题写出逆命题、否命题、逆否命题的关键是什么?
提示:关键是分清楚原命题的条件和结论,然后按照逆命题、否命题、逆否命题的定义来写.【归纳总结】
四种命题的三个关注点
(1)写原命题的逆命题时,不要交换命题的前提条件.
(2)写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.(3)任何一个命题都包含条件和结论两部分,通过条件和结论的不同变换都可以得到这个命题的逆命题、否命题和逆否命题.因此任何一个命题都有逆命题、否命题和逆否命题.
易错警示:对条件或结论进行否定时易出现错误.如“大于”的否定应是“不大于,即≤”;“都是”的否定为“不都是”等.类型一 四种命题的概念
【典例】1.(2015·山东高考)设m∈R,命题“若m>0,则方程x2+x-m=0有实根”的逆否命题是 ( )
A.若方程x2+x-m=0有实根,则m>0
B.若方程x2+x-m=0有实根,则m≤0
C.若方程x2+x-m=0没有实根,则m>0
D.若方程x2+x-m=0没有实根,则m≤02.若命题p的逆命题是q,q的逆否命题是r,则命题r是命题p的 ( )
A.逆命题 B.否命题
C.逆否命题 D.无法确定【解题探究】
1.一个命题的逆否命题的条件和结论与原命题有什么关系?
提示:把原命题的条件和结论否定后再交换位置.
2.判断四种命题间关系的关键是什么?
提示:各个命题的条件和结论.【解析】1.选D.一个命题的逆否命题是将原命题的条件、结论加以否定,并且加以互换.
2.选B.设命题p为“若a,则b”,由题意得:
命题q:若b,则a
命题r:若?a,则?b
所以命题r是命题p的否命题.【延伸探究】
本例1中命题的逆命题和否命题是什么?
【解析】逆命题:若方程x2+x-m=0有实根,则m>0;
否命题:若m≤0,则方程x2+x-m=0没有实根.【方法技巧】四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.【拓展延伸】常见词语的否定【变式训练】1.命题“若α= ,则tanα=1”的逆否命题是 ( )
A.若α≠ ,则tanα=1
B.若α= ,则tanα≠1
C.若tanα≠1,则α≠
D.若tanα≠1,则α=【解析】选C.交换原命题的条件和结论并同时否定,即得原命题的逆否命题,所以应选C.2.设a,b是向量,命题“若a=-b,则|a|=|b|”的逆命题是 ( )
A.若a≠-b,则|a|≠|b| B.若a=-b,则|a|≠|b|
C.若|a|≠|b|,则a≠-b D.若|a|=|b|,则a=-b
【解析】选D.交换原命题的条件和结论可以得到原命题的逆命题.类型二 四种命题真假的判断
【典例】1.有下列命题:①“若x2+y2=0,则x,y全是0”的否命题;②“全等三角形是相似三角形”的否命题;③“若m≥1,则mx2-2(m+1)x+m+3>0的解集是R”的逆命题;④“若a+7是无理数,则a是无理数”的逆否命题.其中为真命题的是 ( )
A.①②③ B.②③④ C.①③④ D.①④2.已知命题“若m-1
1.典例1①中如何否定“x,y全是0”?
提示:x,y不全是0.
2.典例2中逆命题为真的含义是什么?
提示:可以由1
③逆命题为“若mx2-2(m+1)x+m+3>0的解集为“R”,则m≥1”.
因为当m=0时,解集不是R,所以应有 即m>1.
所以其逆命题是假命题.④逆否命题为“若a不是无理数,则a+7不是无理数”,显然当a是有理数时,a+7也是有理数,故逆否命题为真.
2.由已知得,若1
答案:[1,2]【延伸探究】
本例2中的否命题是什么?
【解析】否命题为:若x≤m-1或x≥m+1,则x≤1或x≥2.【方法技巧】判断四种命题真假的方法
(1)要正确理解四种命题间的相互关系.
(2)正确利用相关知识进行判断推理.
(3)若由p经逻辑推理得出q,则命题“若p,则q”为真;确定“若p,则q”为假时,则只需举一个反例说明即可.【变式训练】命题“若a>b,则ac2>bc2(a,b,c∈R)”与
它的逆命题、否命题、逆否命题中,真命题的个数为
( )
A.0 B.2 C.3 D.4【解析】选B.原命题“若a>b,则ac2>bc2(a,b,c∈R)”为假命题;逆命题“若ac2>bc2,则a>b(a,b,c∈R)”为真命题;否命题“若a≤b,则ac2≤bc2(a,b,c∈R)”为真命题;逆否命题“若ac2≤bc2,则a≤b(a,b,c∈R)”为假命题.【补偿训练】(2016·海淀高二检测)命题“如果直线l垂直于平面α内的两条相交直线,则直线l垂直于平面α”的否命题是________;该否命题是________(填“真”或“假”)命题. 【解析】命题“如果直线l垂直于平面α内的两条相交直线,则直线l垂直于平面α”的否命题是:如果直线l不垂直于平面α内的两条相交直线,则直线l不垂直于平面α;
直线与平面垂直的充要条件是直线与平面内的所有直线都垂直,所以命题的否命题是真命题.答案:如果直线l不垂直于平面α内的两条相交直线,则直线l不垂直于平面α 真自我纠错 逆否命题的改写
【典例】(2016·荆州高二检测)命题:“a,b都是奇数,
则a+b是偶数”的逆否命题是_____________________,
是____(填“真”或“假”)命题.【失误案例】分析解题过程,找出错误之处,并写出正确答案.
提示:错误的根本原因是否定“都是”时出现错误,从而导致真假性判断错误,“都是”应否定为“不都是”.【解析】逆否命题:若a+b不是偶数,则a,b不都是奇数.是真命题.
答案:若a+b不是偶数,则a,b不都是奇数 真
