2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件1新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.1.1曲线与方程的概念课件1新人教B版选修2_1(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 367.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:09:07 | ||
图片预览






文档简介
课件14张PPT。 曲线与方程一、复习回顾 在前面我们研究了直线和圆的方程.
1.经过点P(0,b)和斜率为k的直线L的方程
为____________
2.在直角坐标系中,平分第一、三象限的
直线方程是______________
3.圆心为C(a,b) ,半径为r的圆C的方程
为_______________________.x-y=0点的横坐标与纵坐标相等x=y(或x- y=0)第一、三象限角平分线含有关系:(2)以方程x-y=0的解为坐标的点都在 上曲线条件方程坐标系中,平分第一、三象限的直线方程是x-y=0二、思考(1)曲线上点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都在曲线上.
那么,这个方程叫做曲线的方程;
这条曲线叫做方程的曲线.曲线的方程—反映的是图形所满足的数量关系;
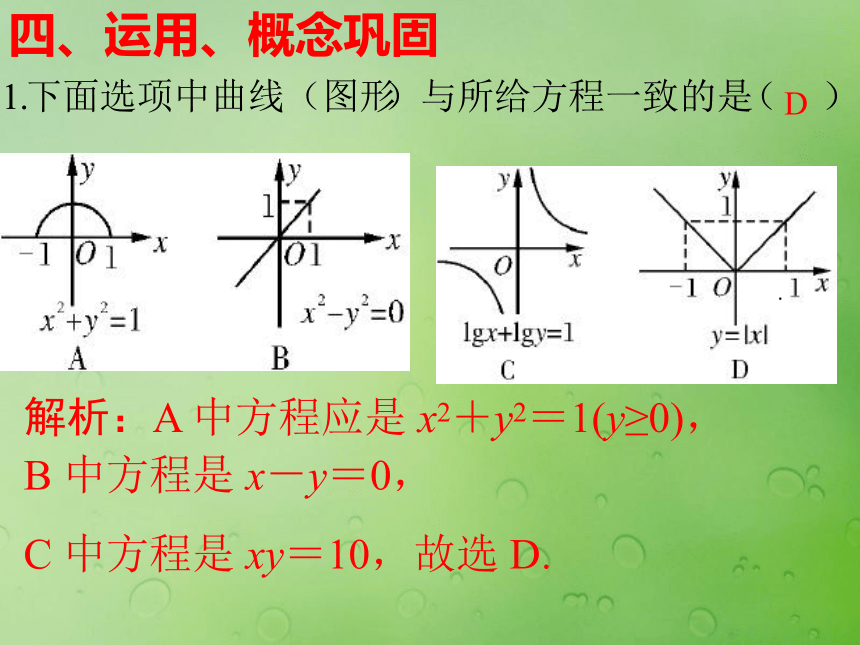
方程的曲线—反映的是数量关系所表示的图形.定义: 一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:说明:三、归纳、生成概念由曲线的方程的定义可知:如果曲线C的方程是 f(x,y)=0,那么点P0(x0 ,y0)在曲线C 上的 充要条件 是f(x0, y0)=0 解析:A 中方程应是 x2+y2=1(y≥0),
B 中方程是 x-y=0,
C 中方程是 xy=10,故选 D.
D.四、运用、概念巩固证明:(1)设M(x0,y0)是圆上任意一点.因为点M到坐标原点的距离等于2,所以
也就是xo2 +yo2 = 4.?
即 (x0,y0) 是方程x2 +y2 = 4的解.(2)设 (x0,y0) 是方程x2 +y2 = 4的解,那么x02 +y02 = 4
两边开方取算术根,得
即点M (x0,y0)到坐标原点的距离等于2,点M (x0,y0)是这个圆上的一点.由(1)(2)可知,x2+y2=4,是以原点为圆心,半径等于2的圆的方程.第一步,设 M (x0,y0)是曲线C上任一点,
证明(x0,y0)是f(x,y)=0的解;归纳:证明已知曲线的方程的方法和步骤:第二步,设(x0,y0)是 f(x,y)=0的解,
证明点 M (x0,y0)在曲线C上.求曲线的方程 我们已经建立了曲线的方程、方程的曲线的概念.利用这两个重要概念,就可以借助于坐标系,用坐标表示点,把曲线看成满足某种条件的点的集合或轨迹,用曲线上点的坐标(x,y)所满足的方程f(x,y)=0下面我们讨论求曲线方程的问题.由两点间的距离公式,点M所适合条件可表示为:将上式两边平方,整理得:
x+2y-7=0 解:(1)设M(x,y)是线段AB的垂直平分线上任意一点,也就是点M属于集合例题分析解:设则点代入圆方程得:即为所求M的轨迹方程3. 已知一条直线l和它上方的一个点F,点F到l的距离是2,一条曲线也在l的上方,它上面的每一点到F的距离减去到l的距离的差都是2,建立适当的坐标系,求这条曲线的方程.解:取直线l为x轴,过点F且垂直于直线l的直线为y轴,建立坐标系xOy,因为曲线在x轴的上方,所以y>0, 所以曲线的方程是 设点M(x,y)是曲线上任意一点,作MB⊥x轴,垂足是B,那么点M属于集合1、建立适当的直角坐标系,
求什么设什么,设动点的坐标为(x,y)
2、找关系(动点满足的几何等式)
3、列式(将几何等式代数化)
4、化简(化为标准的形式)
5、检验(除去不满足题意的点)五、课堂小结:
由上述例子可以看出,求曲线方程的步聚:
1.经过点P(0,b)和斜率为k的直线L的方程
为____________
2.在直角坐标系中,平分第一、三象限的
直线方程是______________
3.圆心为C(a,b) ,半径为r的圆C的方程
为_______________________.x-y=0点的横坐标与纵坐标相等x=y(或x- y=0)第一、三象限角平分线含有关系:(2)以方程x-y=0的解为坐标的点都在 上曲线条件方程坐标系中,平分第一、三象限的直线方程是x-y=0二、思考(1)曲线上点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都在曲线上.
那么,这个方程叫做曲线的方程;
这条曲线叫做方程的曲线.曲线的方程—反映的是图形所满足的数量关系;
方程的曲线—反映的是数量关系所表示的图形.定义: 一般地,在直角坐标系中,如果某曲线C(看作点的集合或适合某种条件的点的轨迹)上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系:说明:三、归纳、生成概念由曲线的方程的定义可知:如果曲线C的方程是 f(x,y)=0,那么点P0(x0 ,y0)在曲线C 上的 充要条件 是f(x0, y0)=0 解析:A 中方程应是 x2+y2=1(y≥0),
B 中方程是 x-y=0,
C 中方程是 xy=10,故选 D.
D.四、运用、概念巩固证明:(1)设M(x0,y0)是圆上任意一点.因为点M到坐标原点的距离等于2,所以
也就是xo2 +yo2 = 4.?
即 (x0,y0) 是方程x2 +y2 = 4的解.(2)设 (x0,y0) 是方程x2 +y2 = 4的解,那么x02 +y02 = 4
两边开方取算术根,得
即点M (x0,y0)到坐标原点的距离等于2,点M (x0,y0)是这个圆上的一点.由(1)(2)可知,x2+y2=4,是以原点为圆心,半径等于2的圆的方程.第一步,设 M (x0,y0)是曲线C上任一点,
证明(x0,y0)是f(x,y)=0的解;归纳:证明已知曲线的方程的方法和步骤:第二步,设(x0,y0)是 f(x,y)=0的解,
证明点 M (x0,y0)在曲线C上.求曲线的方程 我们已经建立了曲线的方程、方程的曲线的概念.利用这两个重要概念,就可以借助于坐标系,用坐标表示点,把曲线看成满足某种条件的点的集合或轨迹,用曲线上点的坐标(x,y)所满足的方程f(x,y)=0下面我们讨论求曲线方程的问题.由两点间的距离公式,点M所适合条件可表示为:将上式两边平方,整理得:
x+2y-7=0 解:(1)设M(x,y)是线段AB的垂直平分线上任意一点,也就是点M属于集合例题分析解:设则点代入圆方程得:即为所求M的轨迹方程3. 已知一条直线l和它上方的一个点F,点F到l的距离是2,一条曲线也在l的上方,它上面的每一点到F的距离减去到l的距离的差都是2,建立适当的坐标系,求这条曲线的方程.解:取直线l为x轴,过点F且垂直于直线l的直线为y轴,建立坐标系xOy,因为曲线在x轴的上方,所以y>0, 所以曲线的方程是 设点M(x,y)是曲线上任意一点,作MB⊥x轴,垂足是B,那么点M属于集合1、建立适当的直角坐标系,
求什么设什么,设动点的坐标为(x,y)
2、找关系(动点满足的几何等式)
3、列式(将几何等式代数化)
4、化简(化为标准的形式)
5、检验(除去不满足题意的点)五、课堂小结:
由上述例子可以看出,求曲线方程的步聚:
