2018年高中数学第二章圆锥曲线与方程2.1.2由曲线求它的方程、由方程研究曲线的性质课件1新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.1.2由曲线求它的方程、由方程研究曲线的性质课件1新人教B版选修2_1(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览





文档简介
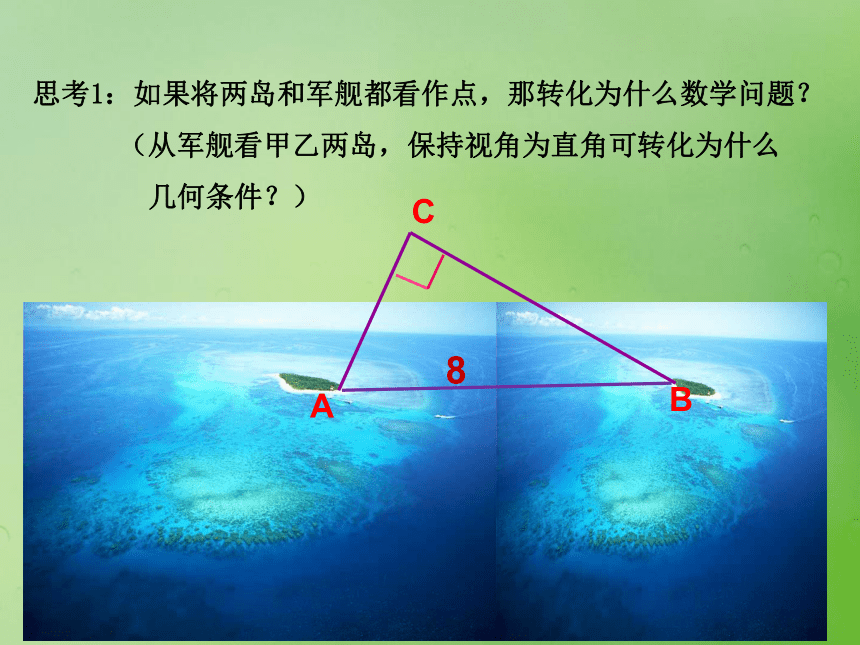
课件14张PPT。求曲线的方程引例:在美丽的南沙群岛中,甲岛与乙岛相距8海里,军舰在海上巡逻,巡逻过程中,从军舰上看甲乙两岛,保持视角为直角,你认为军舰巡逻的路线应是怎样的曲线,你能为它写出一个方程吗? 思考1:如果将两岛和军舰都看作点,那转化为什么数学问题?
(从军舰看甲乙两岛,保持视角为直角可转化为什么
几何条件?)CAB81.什么是曲线的方程和方程的曲线? 答:一般地,在直角坐标系中,如果某曲线C上的点与
一个二元方程 F(x,y)=0的实数解建立了如下的关系:(1)曲线 C 上的点的坐标都是方程 F(x,y)=0 的解,
(2)以方程F(x,y)=0 的解为坐标的点都是曲线C上的点,
那么方程 F(x,y)=0 叫做曲线 C 的方程;
曲线 C 叫做方程 F(x,y)=0 的曲线。知识回顾解析几何研究的主要问题
(1)根据已知条件,求出表示 ;
(2)通过曲线的方程,研究曲线的 .
自学导引3.曲线的方程性质1.
在数学中,通过建立曲线方程,然后用方程研究曲线的方法,叫做坐标法坐标法2.解析几何的定义 用 研究 的知识形成的学科叫解析几何坐标法几何图形题型一 直接法求曲线方程
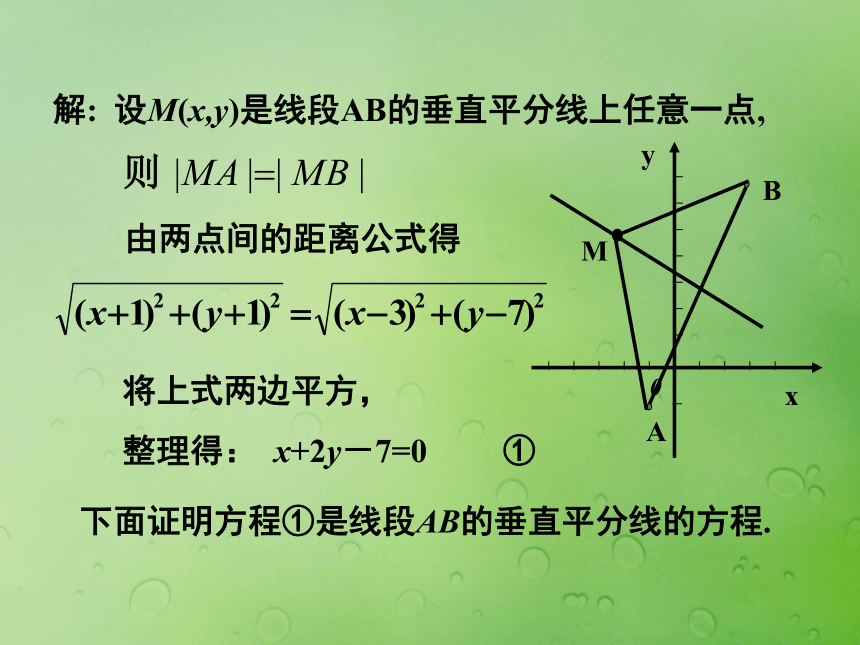
已知点A(-1,-1),点B(3,7),求线段AB
的垂直平分线的方程【例1】思路1:直接求AB的中点及垂直平分线的斜率,
由点斜式即可得解: 设M(x,y)是线段AB的垂直平分线上任意一点,由两点间的距离公式得将上式两边平方,
整理得: x+2y-7=0 ① 下面证明方程①是线段AB的垂直平分线的方程.(1)由求方程的过程可知,垂直平分线上每一点的坐标
都是方程①的解;点M1到A、B的距离分别是即点M1在线段AB的垂直平分线上.由(1)、(2)可知方程①是线段AB的垂直平分线的方程.变式1:已知等腰三角形底边的两个端点是A(-1, -1)
B(3,7) ,求第三个顶点M的轨迹方程.点M的轨迹方程为
x+2y-7=0(x≠1)分析:点M的轨迹为AB的垂直
平分线且不过点(1,3)1、建系(若已给出,本步可省)①建立的坐标系使方程尽可能简单;②尽可能多的使图形上的点(或已知点)落在坐标轴上;③充分利用图形本身的对称性。若曲线是轴对称图形,则可以选它的对称轴为坐标轴,
也可以选取曲线上的特殊点为坐标原点.5. 检验:验证以化简后的方程的解为坐标的点都在曲上.
(一般变为确定 x 、y的范围即可)检验方法:研究运动中的特殊情形或极端情形。(可不证明,但要检验是否产生增解或漏解.)CAB思考2:你觉得应如何建立直角坐标系?
思考3:由角C为直角你能联想到什么? 已知在直角三角形ABC中,角C为直角,斜边AB长为8,建立适当的坐标系,求点C的轨迹方程.分析1:利用M的坐标写出A、 B的
坐标, 再利用两直线垂直分析2:利用M的坐标写出A、 B的坐标,
再利用两直线垂直小结1、求曲线方程的一般步骤:建系设点;列几何式;坐标表示;化简方程;检验说明建系要适当检验要仔细,“多退少补”2、求轨迹方程几种常见方法
(直接法,定义法,待定系数法,相关点法,参数法)3、思想方法:坐标法(数形结合思想)
(从军舰看甲乙两岛,保持视角为直角可转化为什么
几何条件?)CAB81.什么是曲线的方程和方程的曲线? 答:一般地,在直角坐标系中,如果某曲线C上的点与
一个二元方程 F(x,y)=0的实数解建立了如下的关系:(1)曲线 C 上的点的坐标都是方程 F(x,y)=0 的解,
(2)以方程F(x,y)=0 的解为坐标的点都是曲线C上的点,
那么方程 F(x,y)=0 叫做曲线 C 的方程;
曲线 C 叫做方程 F(x,y)=0 的曲线。知识回顾解析几何研究的主要问题
(1)根据已知条件,求出表示 ;
(2)通过曲线的方程,研究曲线的 .
自学导引3.曲线的方程性质1.
在数学中,通过建立曲线方程,然后用方程研究曲线的方法,叫做坐标法坐标法2.解析几何的定义 用 研究 的知识形成的学科叫解析几何坐标法几何图形题型一 直接法求曲线方程
已知点A(-1,-1),点B(3,7),求线段AB
的垂直平分线的方程【例1】思路1:直接求AB的中点及垂直平分线的斜率,
由点斜式即可得解: 设M(x,y)是线段AB的垂直平分线上任意一点,由两点间的距离公式得将上式两边平方,
整理得: x+2y-7=0 ① 下面证明方程①是线段AB的垂直平分线的方程.(1)由求方程的过程可知,垂直平分线上每一点的坐标
都是方程①的解;点M1到A、B的距离分别是即点M1在线段AB的垂直平分线上.由(1)、(2)可知方程①是线段AB的垂直平分线的方程.变式1:已知等腰三角形底边的两个端点是A(-1, -1)
B(3,7) ,求第三个顶点M的轨迹方程.点M的轨迹方程为
x+2y-7=0(x≠1)分析:点M的轨迹为AB的垂直
平分线且不过点(1,3)1、建系(若已给出,本步可省)①建立的坐标系使方程尽可能简单;②尽可能多的使图形上的点(或已知点)落在坐标轴上;③充分利用图形本身的对称性。若曲线是轴对称图形,则可以选它的对称轴为坐标轴,
也可以选取曲线上的特殊点为坐标原点.5. 检验:验证以化简后的方程的解为坐标的点都在曲上.
(一般变为确定 x 、y的范围即可)检验方法:研究运动中的特殊情形或极端情形。(可不证明,但要检验是否产生增解或漏解.)CAB思考2:你觉得应如何建立直角坐标系?
思考3:由角C为直角你能联想到什么? 已知在直角三角形ABC中,角C为直角,斜边AB长为8,建立适当的坐标系,求点C的轨迹方程.分析1:利用M的坐标写出A、 B的
坐标, 再利用两直线垂直分析2:利用M的坐标写出A、 B的坐标,
再利用两直线垂直小结1、求曲线方程的一般步骤:建系设点;列几何式;坐标表示;化简方程;检验说明建系要适当检验要仔细,“多退少补”2、求轨迹方程几种常见方法
(直接法,定义法,待定系数法,相关点法,参数法)3、思想方法:坐标法(数形结合思想)
