2018年高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件2新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.1椭圆的标准方程课件2新人教B版选修2_1(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 374.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:11:03 | ||
图片预览





文档简介
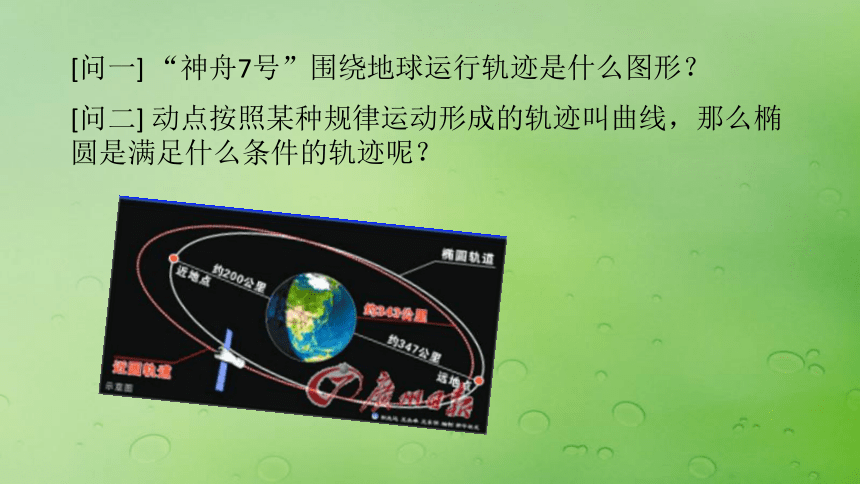
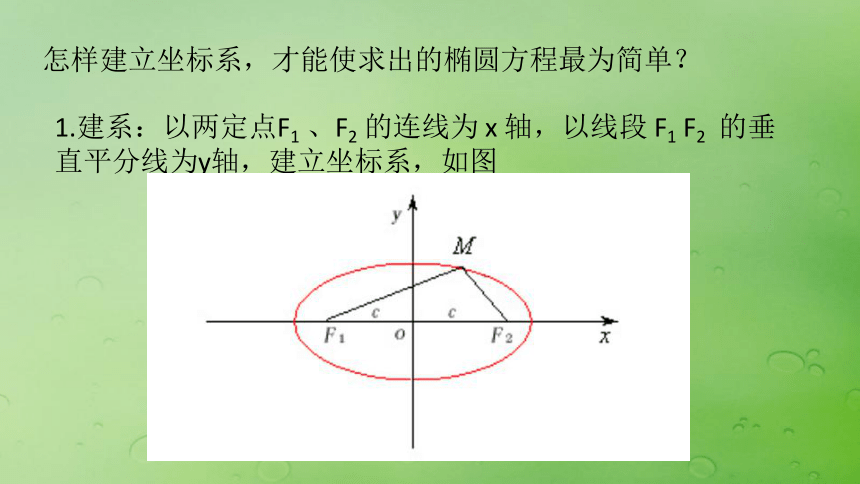
课件14张PPT。椭圆及其标准方程[问一] “神舟7号”围绕地球运行轨迹是什么图形?[问二] 动点按照某种规律运动形成的轨迹叫曲线,那么椭圆是满足什么条件的轨迹呢? 定义 平面内与两个定点F1 、F2 的距离的和等于常数(大于 |F1 F2 | )的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。①平面内(这是大前提);②任意一点到两个定点的距离的和等于常数;③常数大于 |F1 F2 |.1. 求曲线方程的一般步骤是什么?求曲线方程的一般步骤——建系、设点、写出点集、列出方程、化简方程、证明(可省略)2. 建立坐标系的一般原则有哪些?建系的一般原则为:使已知点的坐标和曲线的方程尽可能简单,即原点取在定点或定线段的中点,坐标轴取在定直线上或图形的对称轴上,充分利用图形的对称性.怎样建立坐标系,才能使求出的椭圆方程最为简单?1.建系:以两定点F1 、F2 的连线为 x 轴,以线段 F1 F2 的垂直平分线为y轴,建立坐标系,如图2.设点:
设M ( x , y ) 为椭圆上任意一点,| F1 F2 | = 2 c (c>0) ,则有F1(-c, 0)、F2 (c ,0). 又设 M与F1 和F2 的距离的和等于常数 2 a ( a > 0 ) .3.列出方程4.化简方程:
得到 (a 2 - c 2 ) x 2 + a 2 y 2 = a 2 (a 2 - c 2 ) 令a2-c2=b2令a2-c2=b2两边同除以a2b2得椭圆标准方程此时,椭圆的焦点在x轴上,F1(-c,0),F2(c,0),这里,c2=a2-b2 [问 五] 如果焦点F1 、F2 在 y 轴上,并且点O 与线段F1 F2 的中点重合,a、b、c 的意义同上,椭圆的方程形式又如何呢? 此时,椭圆的焦点在y轴上,F1(0,-c),F2(0,c),这里,c2=a2-b2例 题
1. 判定下列椭圆的焦点在哪个轴上,并指明 a2,b2 和焦点坐标.(1)(2)(1)焦点在x轴 a2=25 b2=16 F1(-3,0) F2(3,0)(2)焦点在y轴 a2=m2+1 b2=m2 F1(0,-1) F2(0,1)2.椭圆2x2+3y2=1焦点坐标为________________. F1(- ,0) F2( ,0)3.椭圆 的焦距是________,焦点坐标为_________;若AB是过左焦点F1的弦,则△F1AB的周长是__________. 2c=8 F1(0,-4) F2(0,4) 201.椭圆上一点P到焦点F1的距离等于6,则点P到另一个焦点F2的距离是__________.
2.动点P到定点F1(-5,0),F2(5,0)的距离的和是10,则动点P的轨迹为( )
(A)椭圆 (B) 线段F1F2 (C) 直线F1F2 (D)不能确定
3.简化方程:
4.椭圆mx2+ny2=-mn (m2. 椭圆的标准方程(注意焦点的位置与方程形式的关系)
3. 解析几何的基本思想 课后作业1. 课本习题 p36练习第 1 、2、3题
2. 课后探究题:将推导椭圆方程过程中得到的方程
变形为
后观察式子的几何意义,提出合理猜想。再见!!
设M ( x , y ) 为椭圆上任意一点,| F1 F2 | = 2 c (c>0) ,则有F1(-c, 0)、F2 (c ,0). 又设 M与F1 和F2 的距离的和等于常数 2 a ( a > 0 ) .3.列出方程4.化简方程:
得到 (a 2 - c 2 ) x 2 + a 2 y 2 = a 2 (a 2 - c 2 ) 令a2-c2=b2令a2-c2=b2两边同除以a2b2得椭圆标准方程此时,椭圆的焦点在x轴上,F1(-c,0),F2(c,0),这里,c2=a2-b2 [问 五] 如果焦点F1 、F2 在 y 轴上,并且点O 与线段F1 F2 的中点重合,a、b、c 的意义同上,椭圆的方程形式又如何呢? 此时,椭圆的焦点在y轴上,F1(0,-c),F2(0,c),这里,c2=a2-b2例 题
1. 判定下列椭圆的焦点在哪个轴上,并指明 a2,b2 和焦点坐标.(1)(2)(1)焦点在x轴 a2=25 b2=16 F1(-3,0) F2(3,0)(2)焦点在y轴 a2=m2+1 b2=m2 F1(0,-1) F2(0,1)2.椭圆2x2+3y2=1焦点坐标为________________. F1(- ,0) F2( ,0)3.椭圆 的焦距是________,焦点坐标为_________;若AB是过左焦点F1的弦,则△F1AB的周长是__________. 2c=8 F1(0,-4) F2(0,4) 201.椭圆上一点P到焦点F1的距离等于6,则点P到另一个焦点F2的距离是__________.
2.动点P到定点F1(-5,0),F2(5,0)的距离的和是10,则动点P的轨迹为( )
(A)椭圆 (B) 线段F1F2 (C) 直线F1F2 (D)不能确定
3.简化方程:
4.椭圆mx2+ny2=-mn (m
3. 解析几何的基本思想 课后作业1. 课本习题 p36练习第 1 、2、3题
2. 课后探究题:将推导椭圆方程过程中得到的方程
变形为
后观察式子的几何意义,提出合理猜想。再见!!
