2018年高中数学第二章圆锥曲线与方程2.4.1抛物线的标准方程课件3新人教B版选修2_1(17张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.4.1抛物线的标准方程课件3新人教B版选修2_1(17张) |
|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:12:27 | ||
图片预览




文档简介
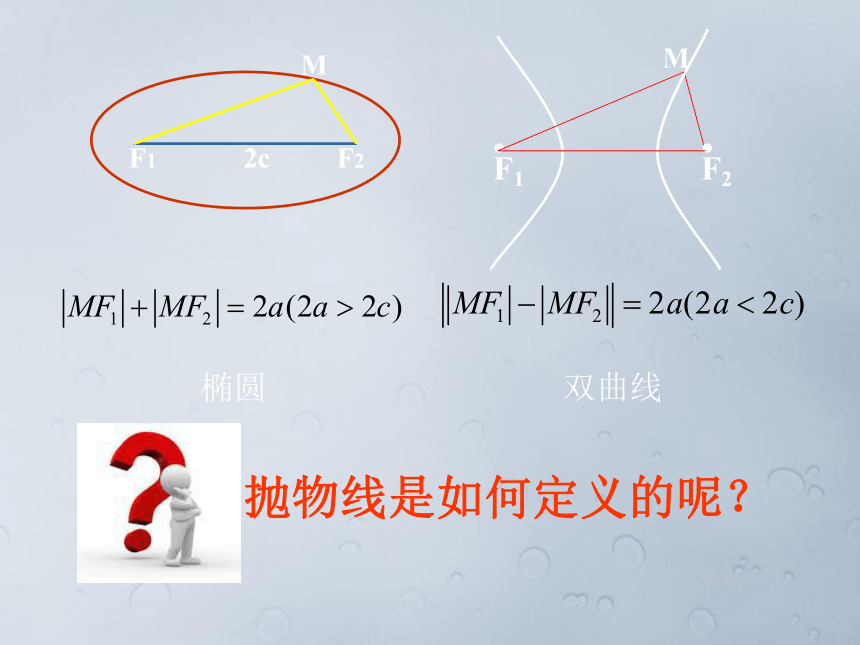
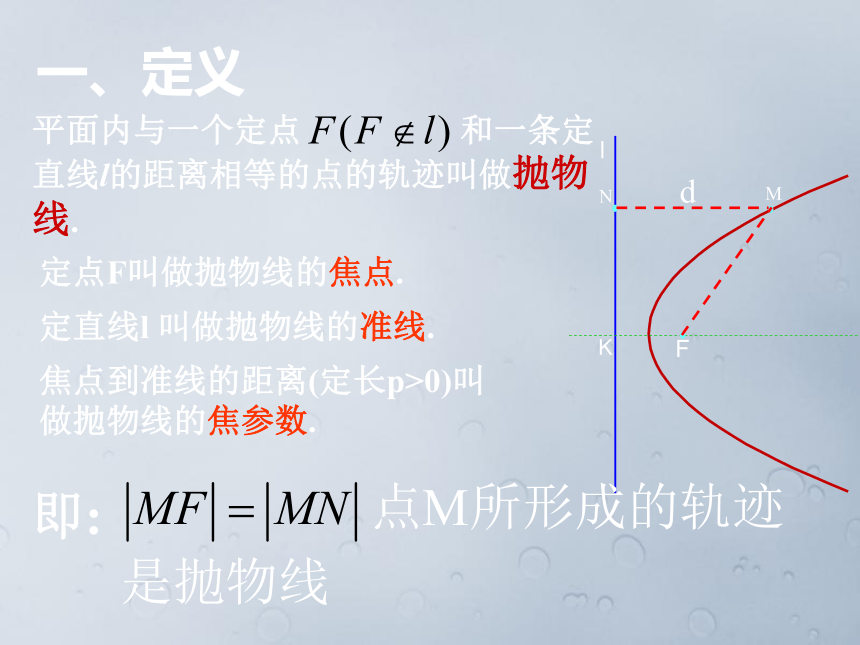
课件17张PPT。生活中存在着各种形式的抛物线抛物线及其标准方程抛物线是如何定义的呢?结论:抛物线上的点到定点F的距离与到定直线 的距离相等一、定义d平面内与一个定点 和一条定直线l的距离相等的点的轨迹叫做抛物 线.定点F叫做抛物线的焦点.定直线l 叫做抛物线的准线.焦点到准线的距离(定长p>0)叫做抛物线的焦参数.用坐标法求点的轨迹方程步骤建立适当的直角坐标系
设动点坐标
列关系式
化简
检验
二、标准方程如何建立直角
坐标系?想一想lFKMNx0y二、标准方程其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离lFKMNyx0例1 已知抛物线的焦点是F(3,0),写出它的标准方程和准线方程例2 已知抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,求抛物线的标准方程以及焦点坐标和准线方程练习1 求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y2 = ax (a>0)
(3)x= —y2 (4)2y2 - 6x =0 (5 , 0)x = - 5x = - 2(2 , 0)18注:必须把方程变成标准形式再进行解答练习2 写出下列抛物线的标准方程(1)焦点F (3,0)
(2)准线方程为 x=- —23练习3 已知点M与点F(4,0)的距离比它到直线 的距离小2,求点M的轨迹方程.
讨论:当焦点在x轴负半轴、y轴正半轴及 y轴负半轴时抛物线的标准方程的形式如何?焦点坐标、准线方程又是多少?小 结 :1、抛物线的定义2、抛物线的标准方程3、焦点坐标以及准线方程4、参数p的几何意义
设动点坐标
列关系式
化简
检验
二、标准方程如何建立直角
坐标系?想一想lFKMNx0y二、标准方程其中p为正常数,它的几何意义是
焦 点 到 准 线 的 距 离lFKMNyx0例1 已知抛物线的焦点是F(3,0),写出它的标准方程和准线方程例2 已知抛物线的焦点在x轴的正半轴上,焦点到准线的距离是3,求抛物线的标准方程以及焦点坐标和准线方程练习1 求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y2 = ax (a>0)
(3)x= —y2 (4)2y2 - 6x =0 (5 , 0)x = - 5x = - 2(2 , 0)18注:必须把方程变成标准形式再进行解答练习2 写出下列抛物线的标准方程(1)焦点F (3,0)
(2)准线方程为 x=- —23练习3 已知点M与点F(4,0)的距离比它到直线 的距离小2,求点M的轨迹方程.
讨论:当焦点在x轴负半轴、y轴正半轴及 y轴负半轴时抛物线的标准方程的形式如何?焦点坐标、准线方程又是多少?小 结 :1、抛物线的定义2、抛物线的标准方程3、焦点坐标以及准线方程4、参数p的几何意义
