2018年高中数学第三章空间向量与立体几何3.1.4空间向量的直角坐标运算课件2新人教B版选修2_1(21张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.1.4空间向量的直角坐标运算课件2新人教B版选修2_1(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 451.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览








文档简介
课件21张PPT。§3.1.4 空间向量的直角坐标运算空间向量基本定理 思 考:空间向量的基本定理是由什么类比
推广而得到的呢?在平面直角坐标系中如何用坐标表示
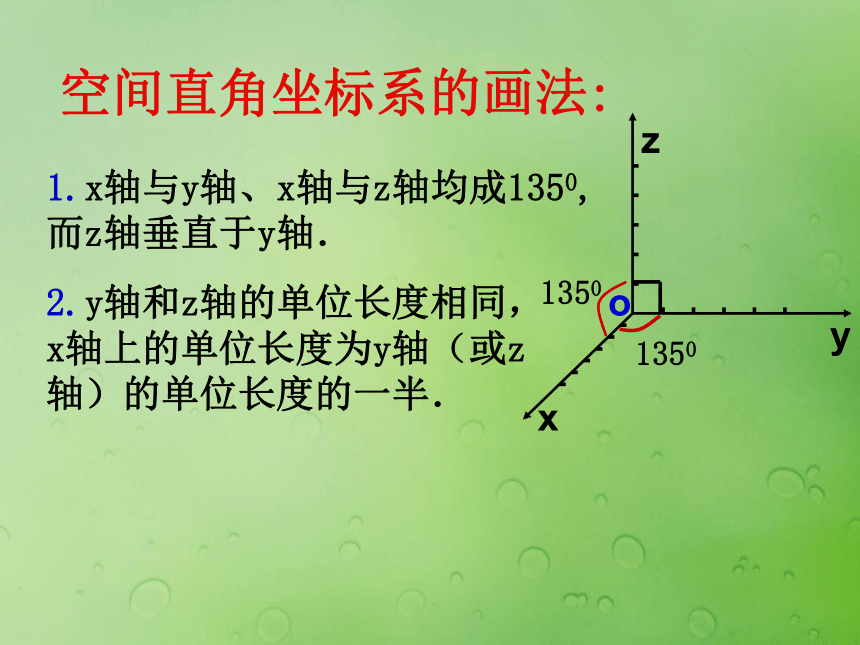
向量呢?思 考:一、空间直角坐标系空间直角坐标系的画法:o1.x轴与y轴、x轴与z轴均成1350,
而z轴垂直于y轴.2.y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半. 这三个互相垂直的单位向量构成空间向量的一个基底{i, j, k}这个基底叫做单位正交基底,单位向量i, j, k都叫做坐标向量. 在空间直角坐标系Oxyz中,已知任一向量a,根据空间向量分解定理,存在唯一数组(x,y,z),使分别为向量a在i,j,k方向上的分向量,思 考:平面向量用坐标表示后,平面向量
有哪些线性运算法则?如何类比推
广到空间呢?利用学过的知识,你能类比猜想出空间向量运算的坐标表示吗?动动脑,动动手,你会得到意想不到的收获例1
已知a=(1,-4,8),b=(3,10,-4),求a+b,
a·b,3a-2b. a+b=(1,-4,8)+ (3,10,-4)
=(1+3,-4+10,8-4)
=(4,6,4) a·b = (1,-4,8) · (3,10,-4)=3-40-32=-69 3a-2b =3 (1,-4,8)-2 (3,10,-4)
=(-3,-32,32)变式已知a+b=(1,-4,8),a-b=(3,10,-4),求3a-2b法一:
由a+b=(1,-4,8),a-b=(3,10,-4),
得2a=(a+b)+(a-b)=(4,6,4);
2b=(a+b)-(a-b)=(-2,-14,12);
即a=(2,3,2);b=(-1,-7,6);
所以3a-2b=(8,23,-6)法二:
设3a-2b=m(a+b)+n(a-b)
=(m+n)a+(m-n)b
则m+n=3,m-n=-2;
m=1/2,n=5/2;
所以3a-2b=1/2(a+b)+5/2(a-b)
=(8,23,-6)(-2,3,1)(2,-4,1)(4,-8,2)(10,1,8)(12,-3,9)变式训练,提高能力变1:已知空间四点A(-2,3,1),B(2,-5,3),C(10,0,10),
D(8,4,9),求证四边形ABCD是梯形。变式训练,提高能力 变2.已知空间四点A(-2,3,1),B(2,-5,3),C(10,n,10),
D(8,4,m),又四边形ABCD是梯形,且AB∥CD,
求实数m,n的值。 例3:已知向量a=(-2,2,0),b=(-2,0,2) ,求向量n
使n⊥a ,且n⊥b .已知A(1,0,1)、B(4,4,6)、C(2,2,3)、D(10,14,17),
且AD=xAB+yAC,则x+y=________.5已知a=(1,5,-1),b=(-2,3,5).
(1)若(ka+b)∥(a-3b),求k.
(2)若(ka+b)⊥(a-3b),求k.-1/3106/3已知a=(1,5,-1),b=(-2,3,5).
(1)若(ka+b)∥(a-3b),求k.
(2)若(ka+b)⊥(a-3b),求k.-1/3106/3回顾反思 总结提炼知识总结:
1.如何用坐标表示空间向量;
2.空间向量坐标运算法则;
方法提炼:
1.类比推广 2.数形结合
3.方程思想 4.整体思想
推广而得到的呢?在平面直角坐标系中如何用坐标表示
向量呢?思 考:一、空间直角坐标系空间直角坐标系的画法:o1.x轴与y轴、x轴与z轴均成1350,
而z轴垂直于y轴.2.y轴和z轴的单位长度相同,x轴上的单位长度为y轴(或z轴)的单位长度的一半. 这三个互相垂直的单位向量构成空间向量的一个基底{i, j, k}这个基底叫做单位正交基底,单位向量i, j, k都叫做坐标向量. 在空间直角坐标系Oxyz中,已知任一向量a,根据空间向量分解定理,存在唯一数组(x,y,z),使分别为向量a在i,j,k方向上的分向量,思 考:平面向量用坐标表示后,平面向量
有哪些线性运算法则?如何类比推
广到空间呢?利用学过的知识,你能类比猜想出空间向量运算的坐标表示吗?动动脑,动动手,你会得到意想不到的收获例1
已知a=(1,-4,8),b=(3,10,-4),求a+b,
a·b,3a-2b. a+b=(1,-4,8)+ (3,10,-4)
=(1+3,-4+10,8-4)
=(4,6,4) a·b = (1,-4,8) · (3,10,-4)=3-40-32=-69 3a-2b =3 (1,-4,8)-2 (3,10,-4)
=(-3,-32,32)变式已知a+b=(1,-4,8),a-b=(3,10,-4),求3a-2b法一:
由a+b=(1,-4,8),a-b=(3,10,-4),
得2a=(a+b)+(a-b)=(4,6,4);
2b=(a+b)-(a-b)=(-2,-14,12);
即a=(2,3,2);b=(-1,-7,6);
所以3a-2b=(8,23,-6)法二:
设3a-2b=m(a+b)+n(a-b)
=(m+n)a+(m-n)b
则m+n=3,m-n=-2;
m=1/2,n=5/2;
所以3a-2b=1/2(a+b)+5/2(a-b)
=(8,23,-6)(-2,3,1)(2,-4,1)(4,-8,2)(10,1,8)(12,-3,9)变式训练,提高能力变1:已知空间四点A(-2,3,1),B(2,-5,3),C(10,0,10),
D(8,4,9),求证四边形ABCD是梯形。变式训练,提高能力 变2.已知空间四点A(-2,3,1),B(2,-5,3),C(10,n,10),
D(8,4,m),又四边形ABCD是梯形,且AB∥CD,
求实数m,n的值。 例3:已知向量a=(-2,2,0),b=(-2,0,2) ,求向量n
使n⊥a ,且n⊥b .已知A(1,0,1)、B(4,4,6)、C(2,2,3)、D(10,14,17),
且AD=xAB+yAC,则x+y=________.5已知a=(1,5,-1),b=(-2,3,5).
(1)若(ka+b)∥(a-3b),求k.
(2)若(ka+b)⊥(a-3b),求k.-1/3106/3已知a=(1,5,-1),b=(-2,3,5).
(1)若(ka+b)∥(a-3b),求k.
(2)若(ka+b)⊥(a-3b),求k.-1/3106/3回顾反思 总结提炼知识总结:
1.如何用坐标表示空间向量;
2.空间向量坐标运算法则;
方法提炼:
1.类比推广 2.数形结合
3.方程思想 4.整体思想
