2018年高中数学第三章空间向量与立体几何3.2.1直线的方向向量与直线的向量方程课件新人教B版选修2_1(30张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2.1直线的方向向量与直线的向量方程课件新人教B版选修2_1(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 959.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:13:58 | ||
图片预览




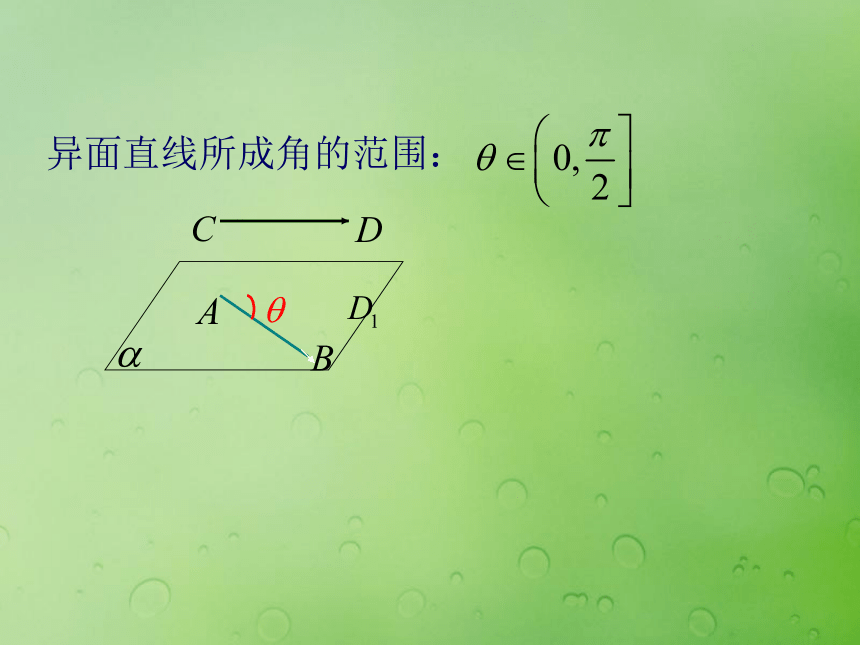



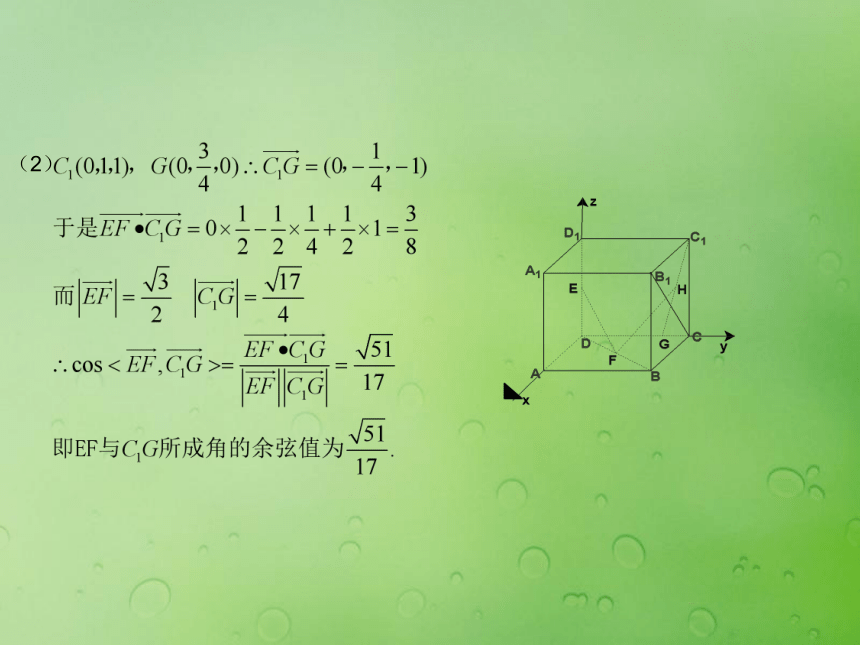


文档简介
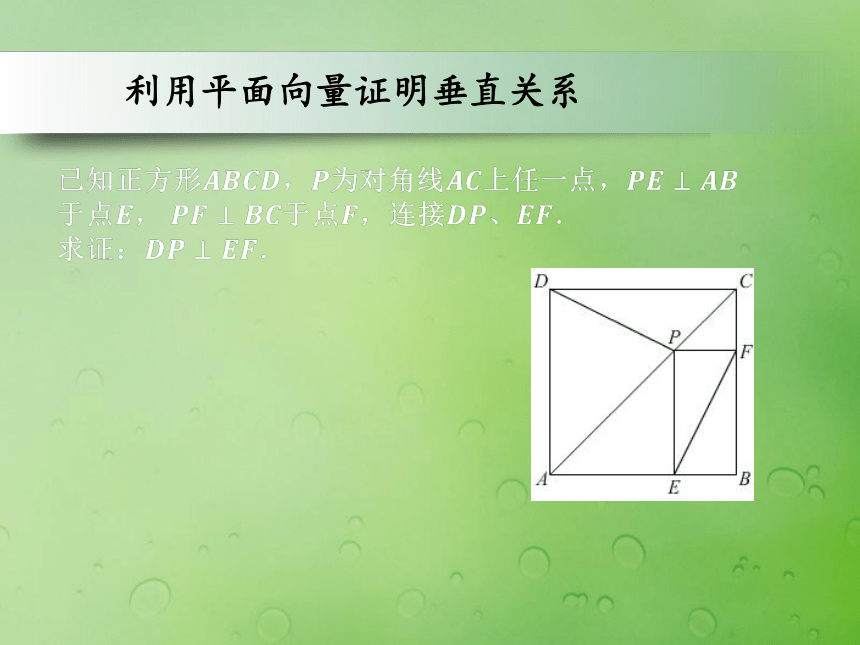
课件30张PPT。3.2.1直线的方向向量与直线的向量方程 用向量证明两条直线垂直和求两直线夹角?利用平面向量证明垂直关系教学目标1.掌握利用向量法证明两条直线垂直和求两条异面直线所成角的重要方法;
2.通过本节课的学习,体会向量法在处理立体几何问题中的重要作用;
3.提高分析与推理能力和空间想象能力.2.什么是直线的方向向量?直线的方向用一个与该直线平行的非零向量来表示,该向量称为这条直线的一个方向向量。 一、复习回顾 已知两条异面直线a,b,经过空间任一点O作直线m//a,n//b;我们把m与n所成的锐角(或直角)叫做异面直线a与b所成的角。3、什么是异面直线及其夹角?夹角范围呢? 不同在任何平面的直线叫做异面直线异面直线所成角的范围: 二、探究新知小组讨论?我们用向量的方法也可以求空间两条直线的夹角和证明空间两条直线垂直(当夹角为90°时)设直线 和 的方向向量分别为 和 ,则设两条直线所成角为θ,则三、典例分析(2)坐标法求异面直线所成的角步骤:1.利用图形中的垂直关系建立空间直角坐标系
2.准确的标出各相关点坐标,并求出各向量的坐标
3.利用向量的数量积公式求出异面直线成角
备注:此法相对简单,关键是建系、找点;务必充分利用题设中的垂直条件(线面垂直、面面垂直)和准确理解图形。方法感悟其他建系方法?返回例2 已知三棱锥O-ABC(如图),OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M,N分别是棱OA,BC的中点,求异面直线MN与AC所成角的余弦。向量法求异面直线所成的角步骤:1.用基底来表示两条异面直线上的向量
2.找出这些基底的长度及相互之间的夹角
3.利用向量数量积公式求出夹角
注意:异面直线所成的角与向量的夹角不同
方法感悟四、课堂检测BB参考图形参考图形返回题目返回题目3、如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,求直线AM与CN所成的角的余弦值.求异面直线所成的角,可以先建立空间直角坐标系,求出直线AM与NC的方向向量的坐标形式,再利用向量的夹角公式计算即可. 课堂小结1.用空间向量证明空间的垂直关系及求异面直线所成的角;
2. 方法:
(1)坐标法:用向量计算或证明几何问题时,可以先建立直角坐标系,然后把向量、点坐标化,借助向量的直角坐标运算法则进行计算或证明;
(2)向量法:用基底表示向量,进行运算
收获:2.用向量方法研究几何问题,需要用向量的观点看问题,将几何问题化归为向量问题来解决.它既是一种数学思想,也是一种数学能力.其中合理设置向量,并建立向量关系,是解决问题的关键.
2.通过本节课的学习,体会向量法在处理立体几何问题中的重要作用;
3.提高分析与推理能力和空间想象能力.2.什么是直线的方向向量?直线的方向用一个与该直线平行的非零向量来表示,该向量称为这条直线的一个方向向量。 一、复习回顾 已知两条异面直线a,b,经过空间任一点O作直线m//a,n//b;我们把m与n所成的锐角(或直角)叫做异面直线a与b所成的角。3、什么是异面直线及其夹角?夹角范围呢? 不同在任何平面的直线叫做异面直线异面直线所成角的范围: 二、探究新知小组讨论?我们用向量的方法也可以求空间两条直线的夹角和证明空间两条直线垂直(当夹角为90°时)设直线 和 的方向向量分别为 和 ,则设两条直线所成角为θ,则三、典例分析(2)坐标法求异面直线所成的角步骤:1.利用图形中的垂直关系建立空间直角坐标系
2.准确的标出各相关点坐标,并求出各向量的坐标
3.利用向量的数量积公式求出异面直线成角
备注:此法相对简单,关键是建系、找点;务必充分利用题设中的垂直条件(线面垂直、面面垂直)和准确理解图形。方法感悟其他建系方法?返回例2 已知三棱锥O-ABC(如图),OA=4,OB=5,OC=3,∠AOB=∠BOC=60°,∠COA=90°,M,N分别是棱OA,BC的中点,求异面直线MN与AC所成角的余弦。向量法求异面直线所成的角步骤:1.用基底来表示两条异面直线上的向量
2.找出这些基底的长度及相互之间的夹角
3.利用向量数量积公式求出夹角
注意:异面直线所成的角与向量的夹角不同
方法感悟四、课堂检测BB参考图形参考图形返回题目返回题目3、如图,在棱长为1的正方体ABCD-A1B1C1D1中,M、N分别为A1B1和BB1的中点,求直线AM与CN所成的角的余弦值.求异面直线所成的角,可以先建立空间直角坐标系,求出直线AM与NC的方向向量的坐标形式,再利用向量的夹角公式计算即可. 课堂小结1.用空间向量证明空间的垂直关系及求异面直线所成的角;
2. 方法:
(1)坐标法:用向量计算或证明几何问题时,可以先建立直角坐标系,然后把向量、点坐标化,借助向量的直角坐标运算法则进行计算或证明;
(2)向量法:用基底表示向量,进行运算
收获:2.用向量方法研究几何问题,需要用向量的观点看问题,将几何问题化归为向量问题来解决.它既是一种数学思想,也是一种数学能力.其中合理设置向量,并建立向量关系,是解决问题的关键.
