2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件1新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件1新人教B版选修2_1(14张) |

|
|
| 格式 | zip | ||
| 文件大小 | 761.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览





文档简介
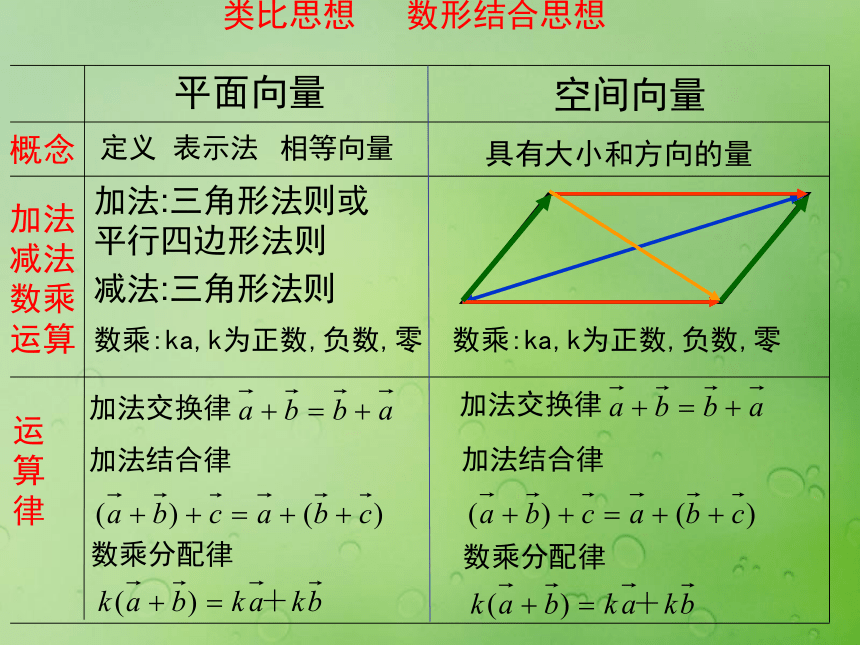
课件14张PPT。空间向量复习 空间向量的引入为代数方法处理立体几何问题提供了一种重要的工具和方法,解题时,可用定量的计算代替定性的分析,从而回避了一些严谨的推理论证,是立体几何的一类重要的问题,也是高考的热点之一。引入:平面向量概念加法
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
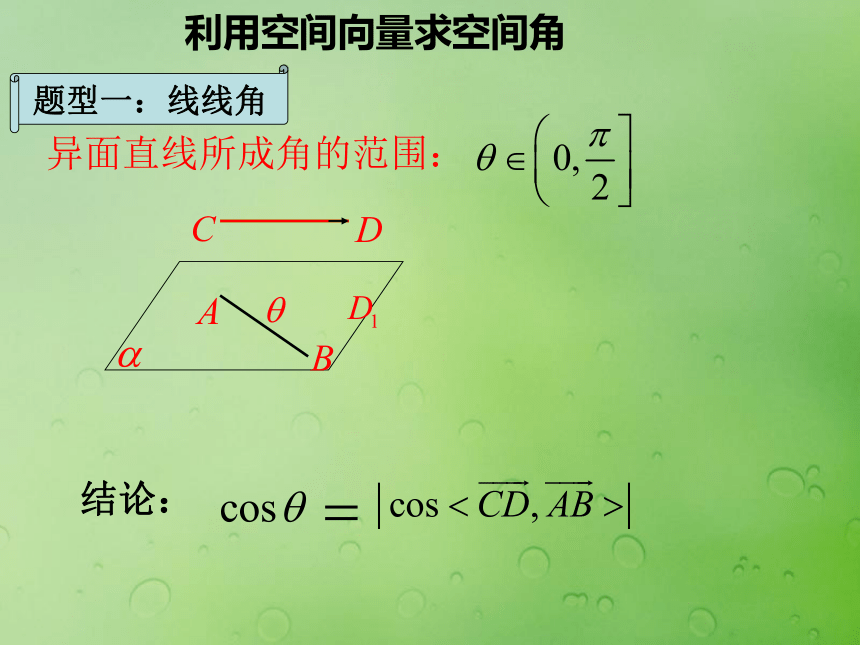
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律类比思想 数形结合思想数乘:ka,k为正数,负数,零前置作业反馈立体几何中的向量方法二、怎样求平面法向量?异面直线所成角的范围: 结论:利用空间向量求空间角题型二:线面角直线与平面所成角的范围: 直线AB与平面α所成的角θ可看成是向量与平面α的法向量所成的锐角的余角,所以有 二面角的范围:关键:观察二面角的范围1、用空间向量解决立体几何问题的“三步曲”。 (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题; (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)
(进行向量运算)(回到图形问题)
各抒己见 百家争鸣链接高考2018强化作业: 在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为AA1上一点.(1)若D为AA1的中点,求证:平面B1CD⊥平面B1C1D;
(2)若二面角B1-DC-C1的大小为60°,求AD的长 请同学们认真完成课后强化作业
减法
数乘
运算运
算
律定义表示法相等向量减法:三角形法则加法:三角形法则或
平行四边形法则空间向量具有大小和方向的量数乘:ka,k为正数,负数,零加法交换律加法结合律数乘分配律类比思想 数形结合思想数乘:ka,k为正数,负数,零前置作业反馈立体几何中的向量方法二、怎样求平面法向量?异面直线所成角的范围: 结论:利用空间向量求空间角题型二:线面角直线与平面所成角的范围: 直线AB与平面α所成的角θ可看成是向量与平面α的法向量所成的锐角的余角,所以有 二面角的范围:关键:观察二面角的范围1、用空间向量解决立体几何问题的“三步曲”。 (1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题; (2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;(3)把向量的运算结果“翻译”成相应的几何意义。(化为向量问题)
(进行向量运算)(回到图形问题)
各抒己见 百家争鸣链接高考2018强化作业: 在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2,D为AA1上一点.(1)若D为AA1的中点,求证:平面B1CD⊥平面B1C1D;
(2)若二面角B1-DC-C1的大小为60°,求AD的长 请同学们认真完成课后强化作业
