2018年高中数学第一章常用逻辑用语1.2.1“且”与“或”课件1新人教B版选修2_1(20张)
文档属性
| 名称 | 2018年高中数学第一章常用逻辑用语1.2.1“且”与“或”课件1新人教B版选修2_1(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 250.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 11:15:33 | ||
图片预览








文档简介
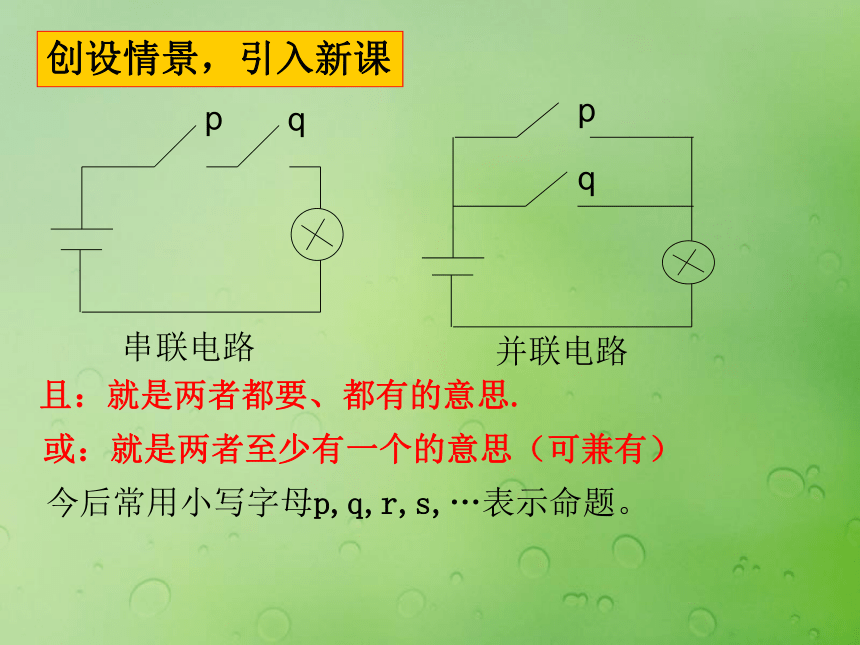
课件20张PPT。§1.2基本逻辑联结词创设情景,引入新课且:就是两者都要、都有的意思.或:就是两者至少有一个的意思(可兼有)今后常用小写字母p,q,r,s,…表示命题。 1.2.1 “且 ”与“或”下列命题中,命题间有什么关系? (1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除;问题1:命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题. 一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q” 1. “且 ”问题2
思考:命题 p∧q的真假如何确定?
观察下列各组命题,命题p∧q的真假与p、q的真假有什么联系? P:12能被3整除;
q:12能被4整除;
p∧q:12能被3整除且能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∧q:等腰三角形两边相等且三条中线相等. P:6是奇数;
q:6是质数;
p∧q:6是奇数且是质数.填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 两个命题中有一个命题是假命题时,p∧q是 .一句话概括:
全真才真,一假则假. 真命题假命题命题p∧q的真假判断方法:假假假真探究:逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢? 对“且”的理解,可联想到集合中“交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思活动探究例1:将下列命题用“且”联结成新命题,并判断他们的真假:
(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
(2)p:菱形的对角线互相垂直,
q:菱形的对角线互相平分;
(3)p:35是15的倍数,q:35是7的倍数. (3) p∧q : 35是15的倍数且是7的倍数.
∵ p是假命题, ∴ p∧q是假命题. (1)p∧q:平行四边形的对角线互相平分且相等.∵q是假命题,∴p∧q是假命题.(2)p∧q :菱形的对角线互相垂直且平分.
∵p、q都是真命题, ∴ p∧q是真命题.例题分析解: 有些命题如含有“……和……”、
“……与……”、“既……,又…..”等词的命题能用“且”改写成“p∧q”的形式,例2:用逻辑联结词“且”改写下列命题,并判断它们的真假.
(1)1既是奇数,又是质数;
(2)2和3都是质数. 解:(1) 1是奇数且1是质数 , 假命题
(2) 2是质数且3是质数,真命题2. 或下列命题中,命题 间有什么关系? (1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.1.问题命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题. 一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.思考:命题 p∨q的真假如何确定?
观察下列三组命题,命题p∨q的真假与p、q 的真假有什么联系? P:27是7的倍数;
q:27是9的倍数;
p∨q :27是7的倍数或是9的倍数.P:等腰梯形对角线垂直;
q:等腰梯形对角线平分;
p∨q:等腰梯形对角线垂直或平分.P:三边对应成比例的两个三角形相似;
q:三角对应相等的两个三角形相似;
p∨q:三边对应成比例或三角对应相等的两 个三角形相似. 一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.一句话概括:
一真即真, 全假才假. 一真假命题p∨q的真假判断方法:假真真真探究:逻辑联结词“或”的含义与集合中学过的哪个概念的意义相同呢? 对“或”的理解,可联想到集合中“并集”的概念.A∪B={x︱x∈A或x∈B}中的“或”,它是指
“x∈A”、“x∈B”中至少一个是成立的,即x∈A且
x B;也可以x A且x∈B;也可以x∈A且x∈B.活动探究例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等. 解:(1)p:2=2 ;q:2<2
∵ p是真命题,∴p∨q是真命题.(3)p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等.
∵命题p、q都是假命题, ∴ p∨q是假命题.(2)p:集合A是A∩B的子集;q:集合A是A∪B的子集
∵q是真命题, ∴p∨q是真命题.例题分析 如果p∧q为真命题,那么p∨q一定是真命题吗?反之,如果p∨q为真命题,那么p∧q一定是真命题吗?总结思考1.命题“方程 的解是 ”中,使用逻辑词的情况是( )
A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C. 使用了逻辑联结词“且”
D. 使用了逻辑联结词“或”与“且”B练习2.在下列命题中
(1)命题“不等式 没有实数解”;
(2)命题“-1是偶数或奇数”;
(3)命题“ 既属于集合 ,也属于集合 ”;
(4)命题“ ”
其中,真命题为_____________.(2)(4)3. 命题p:“不等式 的解集为
”;命题q:“不等式 的解集为 ”,则 ( )
A.p真q假
B.p假q真
C.命题“p且q”为真
D.命题“p或q”为假 D 4.在一次模拟射击游戏中,小李连续射击了两次,设命题p:“第一次射击中靶”,命题q:“第二次射击中靶”,试用,p、q及逻辑联结词“或”“且” 表示下列命题:
(1)两次射击均中靶;
(2)两次射击至少有一次中靶.p∧qp∨q5.设命题p:实数x满足 ,
命题q:实数x满足 ,
若p且q为真,则实数 x的取值
范围为 . (1)掌握逻辑联结词“且、或”的含义
(2)正确应用逻辑联结词“且、或”解决问题
(3)掌握真值表并会应用真值表解决问题
自主总结
(2)12能被4整除;
(3)12能被3整除且能被4整除;问题1:命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题. 一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q” 1. “且 ”问题2
思考:命题 p∧q的真假如何确定?
观察下列各组命题,命题p∧q的真假与p、q的真假有什么联系? P:12能被3整除;
q:12能被4整除;
p∧q:12能被3整除且能被4整除;P:等腰三角形两腰相等;
q:等腰三角形三条中线相等;
p∧q:等腰三角形两边相等且三条中线相等. P:6是奇数;
q:6是质数;
p∧q:6是奇数且是质数.填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 两个命题中有一个命题是假命题时,p∧q是 .一句话概括:
全真才真,一假则假. 真命题假命题命题p∧q的真假判断方法:假假假真探究:逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢? 对“且”的理解,可联想到集合中“交集”的概念.
A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思活动探究例1:将下列命题用“且”联结成新命题,并判断他们的真假:
(1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
(2)p:菱形的对角线互相垂直,
q:菱形的对角线互相平分;
(3)p:35是15的倍数,q:35是7的倍数. (3) p∧q : 35是15的倍数且是7的倍数.
∵ p是假命题, ∴ p∧q是假命题. (1)p∧q:平行四边形的对角线互相平分且相等.∵q是假命题,∴p∧q是假命题.(2)p∧q :菱形的对角线互相垂直且平分.
∵p、q都是真命题, ∴ p∧q是真命题.例题分析解: 有些命题如含有“……和……”、
“……与……”、“既……,又…..”等词的命题能用“且”改写成“p∧q”的形式,例2:用逻辑联结词“且”改写下列命题,并判断它们的真假.
(1)1既是奇数,又是质数;
(2)2和3都是质数. 解:(1) 1是奇数且1是质数 , 假命题
(2) 2是质数且3是质数,真命题2. 或下列命题中,命题 间有什么关系? (1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.1.问题命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题. 一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.思考:命题 p∨q的真假如何确定?
观察下列三组命题,命题p∨q的真假与p、q 的真假有什么联系? P:27是7的倍数;
q:27是9的倍数;
p∨q :27是7的倍数或是9的倍数.P:等腰梯形对角线垂直;
q:等腰梯形对角线平分;
p∨q:等腰梯形对角线垂直或平分.P:三边对应成比例的两个三角形相似;
q:三角对应相等的两个三角形相似;
p∨q:三边对应成比例或三角对应相等的两 个三角形相似. 一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.一句话概括:
一真即真, 全假才假. 一真假命题p∨q的真假判断方法:假真真真探究:逻辑联结词“或”的含义与集合中学过的哪个概念的意义相同呢? 对“或”的理解,可联想到集合中“并集”的概念.A∪B={x︱x∈A或x∈B}中的“或”,它是指
“x∈A”、“x∈B”中至少一个是成立的,即x∈A且
x B;也可以x A且x∈B;也可以x∈A且x∈B.活动探究例3:判断下列命题的真假:
(1)2≤2;
(2)集合A是A∩B的子集或是A∪B的子集;
(3)周长相等的两个三角形全等或面积相等的两个三角形全等. 解:(1)p:2=2 ;q:2<2
∵ p是真命题,∴p∨q是真命题.(3)p:周长相等的两个三角形全等;
q:面积相等的两个三角形全等.
∵命题p、q都是假命题, ∴ p∨q是假命题.(2)p:集合A是A∩B的子集;q:集合A是A∪B的子集
∵q是真命题, ∴p∨q是真命题.例题分析 如果p∧q为真命题,那么p∨q一定是真命题吗?反之,如果p∨q为真命题,那么p∧q一定是真命题吗?总结思考1.命题“方程 的解是 ”中,使用逻辑词的情况是( )
A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C. 使用了逻辑联结词“且”
D. 使用了逻辑联结词“或”与“且”B练习2.在下列命题中
(1)命题“不等式 没有实数解”;
(2)命题“-1是偶数或奇数”;
(3)命题“ 既属于集合 ,也属于集合 ”;
(4)命题“ ”
其中,真命题为_____________.(2)(4)3. 命题p:“不等式 的解集为
”;命题q:“不等式 的解集为 ”,则 ( )
A.p真q假
B.p假q真
C.命题“p且q”为真
D.命题“p或q”为假 D 4.在一次模拟射击游戏中,小李连续射击了两次,设命题p:“第一次射击中靶”,命题q:“第二次射击中靶”,试用,p、q及逻辑联结词“或”“且” 表示下列命题:
(1)两次射击均中靶;
(2)两次射击至少有一次中靶.p∧qp∨q5.设命题p:实数x满足 ,
命题q:实数x满足 ,
若p且q为真,则实数 x的取值
范围为 . (1)掌握逻辑联结词“且、或”的含义
(2)正确应用逻辑联结词“且、或”解决问题
(3)掌握真值表并会应用真值表解决问题
自主总结
