2018年高中数学第1章立体几何初步1.2.3直线与平面的位置关系课件10苏教版必修2(20张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.3直线与平面的位置关系课件10苏教版必修2(20张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 21:52:28 | ||
图片预览







文档简介
(共20张PPT)
苏州虎丘塔
比萨斜塔
伽利略实验
历史悠久250
年
倾斜不倒的意大利精神
860
860
如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。斜线上一点与斜足间的线段叫做这个点到平面的斜线段。
P
A
斜足
斜线
斜线
斜足
射影
垂足
垂线
(1) 一个平面的斜线和它在平面内的射影所成的锐角,叫做斜线和平面所成的角.
定义:
(1)(2)
一条直线垂直于平面,它们所成的角是直角.
一条直线在平面内,或与平面平行,它们所成的角是0°的角.
(2)规定:
练习1.一条直线和平面所成角为θ,那么θ的取值范围是( )
A.0°<θ<90°B.0°≤θ≤90°
C.0°≤θ<90°D.0°≤θ≤180°
【解析】由线面角的定义知B正确.
变式:平面的斜线与平面所成的角的取值范围是
提炼:直线与平面所成的角的取值范围是
B
练习2.过平面外一点作与平面所成角为30°的直线有多少条?
【解析】由圆锥母线与圆锥底面所成角相等知,这样的直线有无数条.
射影结论:由平面外一点向该平面作到平面的斜线段,斜线段等则射影等,射影等则斜线段等
概念辨析,理解新知
A1
B1
C1
D1
A
B
C
D
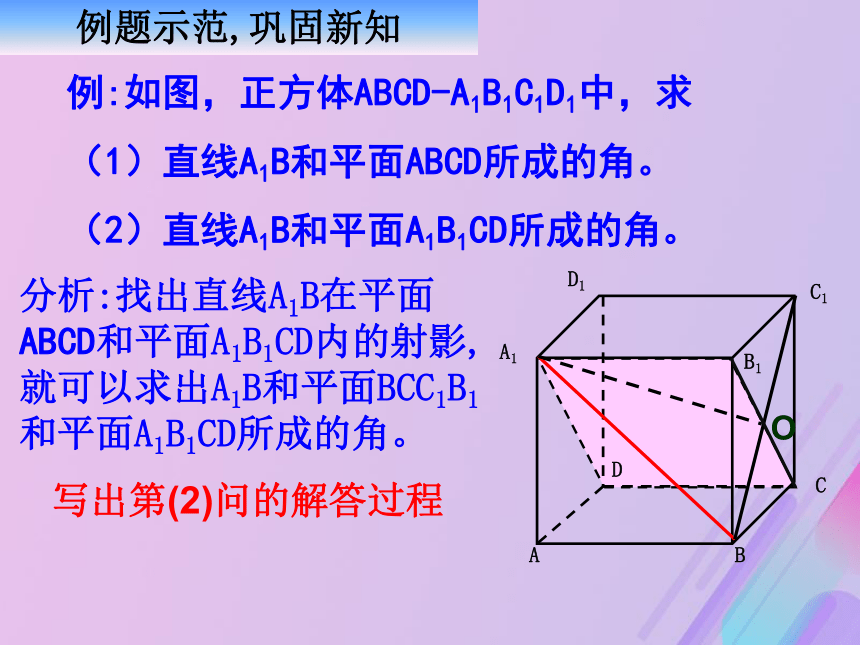
例:如图,正方体ABCD-A1B1C1D1中,求
(1)直线A1B和平面ABCD所成的角。
(2)直线A1B和平面A1B1CD所成的角。
O
例题示范,巩固新知
分析:找出直线A1B在平面 ABCD和平面A1B1CD内的射影,就可以求出A1B和平面BCC1B1和平面A1B1CD所成的角。
写出第(2)问的解答过程
(1)找或作直线在平面内的射影;
关键是找“双足”
—斜足、垂足
(2)利用定义指明线面所成角
线面角
线线角
(3)求线面所成角
一般求解直角三角形
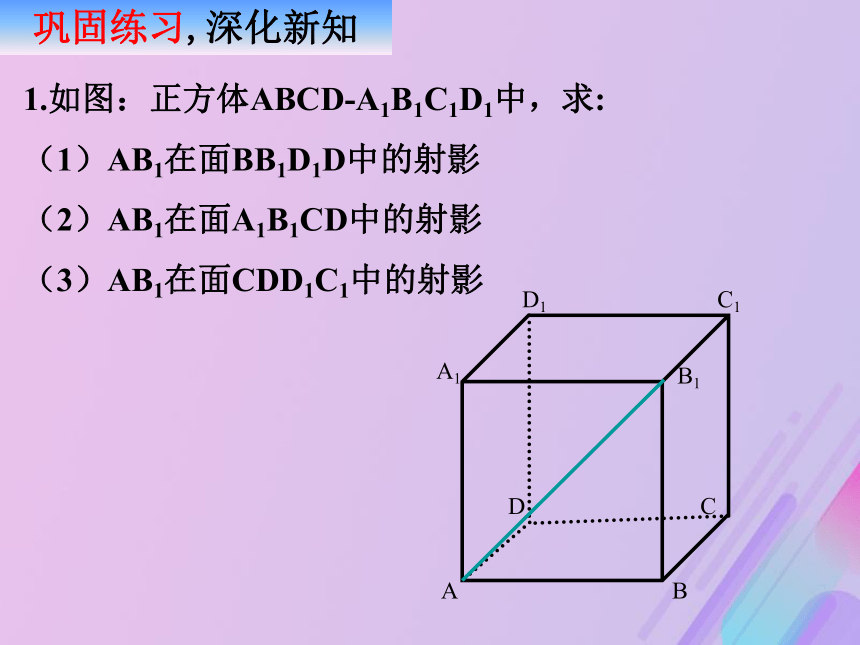
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
巩固练习,深化新知
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
O
线段B1O
巩固练习
巩固练习,深化新知
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
E
线段B1E
巩固练习
巩固练习,深化新知
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
线段C1D
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
0o
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
90o
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
45o
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
E
30o
巩固练习
巩固练习,深化新知
(1)找或作直线在平面内的射影;
线面角
线线角
关键是找“双足”
—斜足、垂足
(3)求线面所成角
一般求解直角三角形
归纳小结,升华新知
(2)利用定义指明线面所成角
(1)识角用角;(2)作角求角
空间问题
平面问题
4.数学思想方法:转化的思想
1.如图,在正方体AC1中,E是棱CC1的中点,
求BE与平面AA1C1C所成角的正弦值.
拓展练习,活化新知
2、 如图,AB⊥BC,AB⊥CD,AB=2,AC与平面BCD所成的角为30°,∠CBD=45°,求直线AC与平面ABD所成角的正弦值.
c
B
A
D
E
思考:直线 与平面 成角 ,若直线 在 内的射影与 内的直线 成角 ,则 与 所成的角是
苏州虎丘塔
比萨斜塔
伽利略实验
历史悠久250
年
倾斜不倒的意大利精神
860
860
如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。斜线上一点与斜足间的线段叫做这个点到平面的斜线段。
P
A
斜足
斜线
斜线
斜足
射影
垂足
垂线
(1) 一个平面的斜线和它在平面内的射影所成的锐角,叫做斜线和平面所成的角.
定义:
(1)(2)
一条直线垂直于平面,它们所成的角是直角.
一条直线在平面内,或与平面平行,它们所成的角是0°的角.
(2)规定:
练习1.一条直线和平面所成角为θ,那么θ的取值范围是( )
A.0°<θ<90°B.0°≤θ≤90°
C.0°≤θ<90°D.0°≤θ≤180°
【解析】由线面角的定义知B正确.
变式:平面的斜线与平面所成的角的取值范围是
提炼:直线与平面所成的角的取值范围是
B
练习2.过平面外一点作与平面所成角为30°的直线有多少条?
【解析】由圆锥母线与圆锥底面所成角相等知,这样的直线有无数条.
射影结论:由平面外一点向该平面作到平面的斜线段,斜线段等则射影等,射影等则斜线段等
概念辨析,理解新知
A1
B1
C1
D1
A
B
C
D
例:如图,正方体ABCD-A1B1C1D1中,求
(1)直线A1B和平面ABCD所成的角。
(2)直线A1B和平面A1B1CD所成的角。
O
例题示范,巩固新知
分析:找出直线A1B在平面 ABCD和平面A1B1CD内的射影,就可以求出A1B和平面BCC1B1和平面A1B1CD所成的角。
写出第(2)问的解答过程
(1)找或作直线在平面内的射影;
关键是找“双足”
—斜足、垂足
(2)利用定义指明线面所成角
线面角
线线角
(3)求线面所成角
一般求解直角三角形
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
巩固练习,深化新知
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
O
线段B1O
巩固练习
巩固练习,深化新知
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
E
线段B1E
巩固练习
巩固练习,深化新知
1.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影
A1
D1
C1
B1
A
D
C
B
线段C1D
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
0o
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
90o
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
45o
巩固练习
巩固练习,深化新知
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角
A1
D1
C1
B1
A
D
C
B
E
30o
巩固练习
巩固练习,深化新知
(1)找或作直线在平面内的射影;
线面角
线线角
关键是找“双足”
—斜足、垂足
(3)求线面所成角
一般求解直角三角形
归纳小结,升华新知
(2)利用定义指明线面所成角
(1)识角用角;(2)作角求角
空间问题
平面问题
4.数学思想方法:转化的思想
1.如图,在正方体AC1中,E是棱CC1的中点,
求BE与平面AA1C1C所成角的正弦值.
拓展练习,活化新知
2、 如图,AB⊥BC,AB⊥CD,AB=2,AC与平面BCD所成的角为30°,∠CBD=45°,求直线AC与平面ABD所成角的正弦值.
c
B
A
D
E
思考:直线 与平面 成角 ,若直线 在 内的射影与 内的直线 成角 ,则 与 所成的角是
