2018年高中数学第1章立体几何初步1.2.4平面与平面的位置关系课件8苏教版必修2(20张)
文档属性
| 名称 | 2018年高中数学第1章立体几何初步1.2.4平面与平面的位置关系课件8苏教版必修2(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 386.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览





文档简介
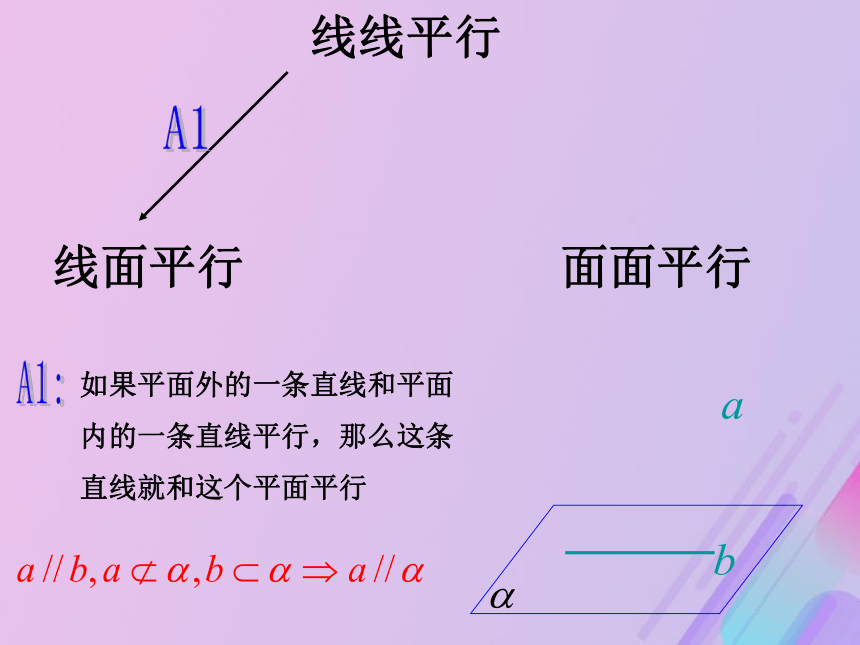
课件20张PPT。空间中的平行关系一、空间中的平行关系线线平行线面平行面面平行A1:如果平面外的一条直线和平面
内的一条直线平行,那么这条
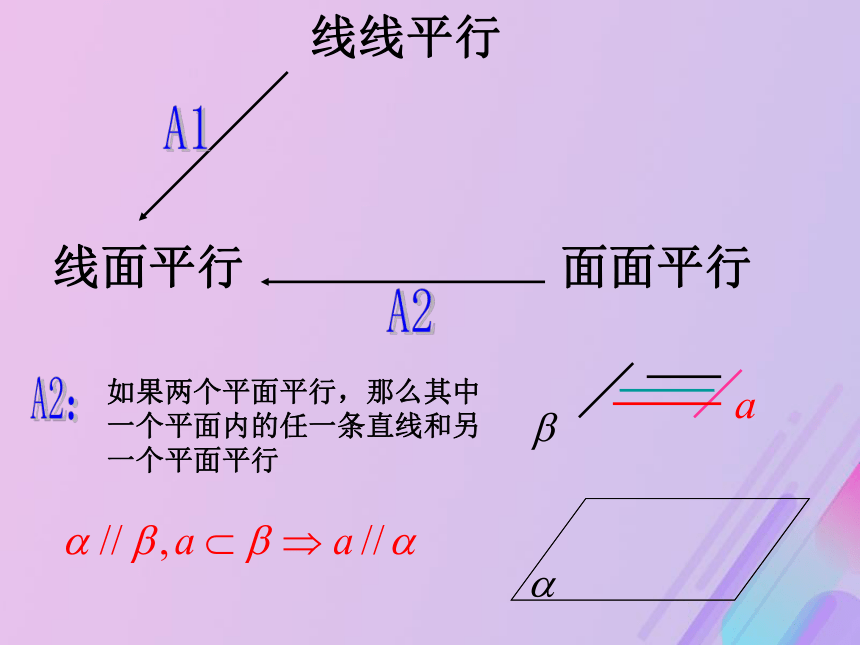
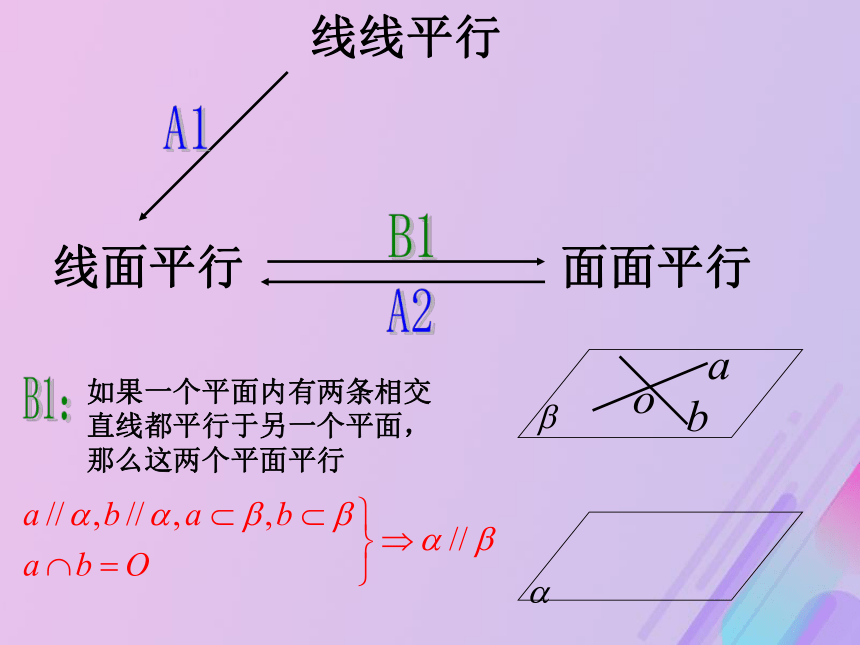
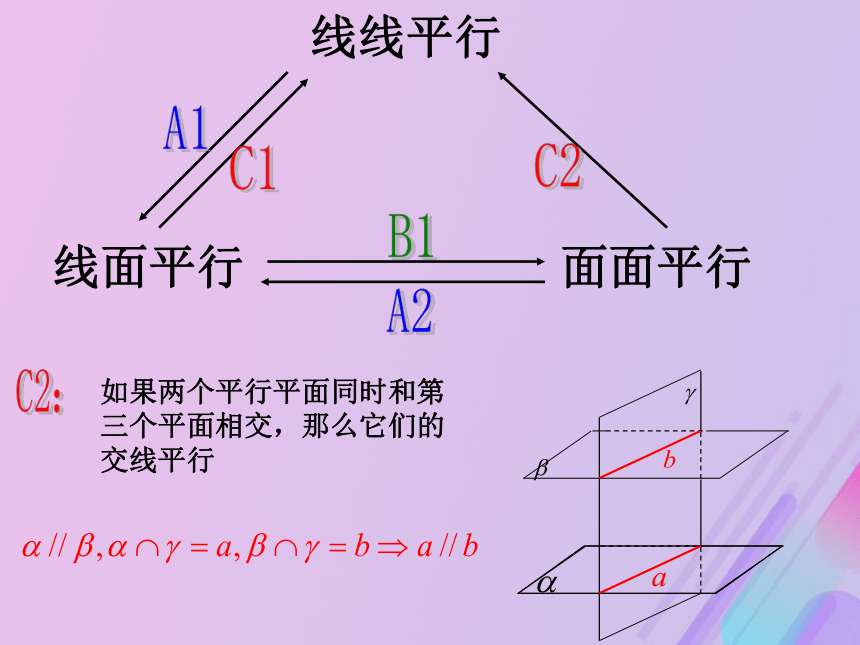
直线就和这个平面平行线线平行线面平行面面平行A1A2:如果两个平面平行,那么其中一个平面内的任一条直线和另一个平面平行线线平行线面平行面面平行A1A2B1:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行线线平行线面平行面面平行A1A2B1C1:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行线线平行线面平行面面平行A1A2C1B1C2:如果两个平行平面同时和第三个平面相交,那么它们的交线平行线线平行线面平行面面平行A1A2C2C1B11、在下面六个命题中:
(1)两条平行线中有一条平行于一个平面,则另一条也平行于这个平面
(2)一条直线平行于平面中的一条直线,则这条直线平行于该平面
(3)一条直线平行于平面中的无数条直线,则这条直线平行于该平面
(4)一条直线与一个平面平行,则这条直线和平面内的所有直线都平行
(5)一条直线与一个平面平行,则这条直线和平面内的无数条直线都平行
(6)过平面外一点只有一条直线和这个平面平行
正确命题的个数为( )二、基础练习√×××××12. 已知a、b、c表示不同的直线,α、β、γ表示不 同的平面,则下列四个命题:
①若a⊥c,b⊥c,则a∥b;
②若c⊥α,c⊥β,则α∥β;
③若a⊥b,b⊥α,且a α,则a∥α;
④若α⊥γ,β⊥γ,则α∥β.
其中真命题的个数为( )个 2×√√×三、典型例题HGABCEDMNFQP【解题回顾】证明线面平行的常用方法是:
(1)证明直线平行于平面内的一条直线;
(2)证明直线所在的平面与已知平面平行.PQE【解题回顾】证明面面平行时,由判定定理要证面面平行只要证线面平行.
如果直接证得一平面内有两相交直线分别平行于另一平面内的两相交直线后就说两面平行,则有失严谨.四、归纳小结线线平行线面平行面面平行
内的一条直线平行,那么这条
直线就和这个平面平行线线平行线面平行面面平行A1A2:如果两个平面平行,那么其中一个平面内的任一条直线和另一个平面平行线线平行线面平行面面平行A1A2B1:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行线线平行线面平行面面平行A1A2B1C1:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行线线平行线面平行面面平行A1A2C1B1C2:如果两个平行平面同时和第三个平面相交,那么它们的交线平行线线平行线面平行面面平行A1A2C2C1B11、在下面六个命题中:
(1)两条平行线中有一条平行于一个平面,则另一条也平行于这个平面
(2)一条直线平行于平面中的一条直线,则这条直线平行于该平面
(3)一条直线平行于平面中的无数条直线,则这条直线平行于该平面
(4)一条直线与一个平面平行,则这条直线和平面内的所有直线都平行
(5)一条直线与一个平面平行,则这条直线和平面内的无数条直线都平行
(6)过平面外一点只有一条直线和这个平面平行
正确命题的个数为( )二、基础练习√×××××12. 已知a、b、c表示不同的直线,α、β、γ表示不 同的平面,则下列四个命题:
①若a⊥c,b⊥c,则a∥b;
②若c⊥α,c⊥β,则α∥β;
③若a⊥b,b⊥α,且a α,则a∥α;
④若α⊥γ,β⊥γ,则α∥β.
其中真命题的个数为( )个 2×√√×三、典型例题HGABCEDMNFQP【解题回顾】证明线面平行的常用方法是:
(1)证明直线平行于平面内的一条直线;
(2)证明直线所在的平面与已知平面平行.PQE【解题回顾】证明面面平行时,由判定定理要证面面平行只要证线面平行.
如果直接证得一平面内有两相交直线分别平行于另一平面内的两相交直线后就说两面平行,则有失严谨.四、归纳小结线线平行线面平行面面平行
