2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件7苏教版必修2(21张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.1直线的斜率课件7苏教版必修2(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 665.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 21:45:20 | ||
图片预览






文档简介
课件21张PPT。直线的斜率和倾斜角复习引入一次函数y=kx+b的图象有什么特征?问题1:一次函数y=kx+b的图象是一条直线.答:直线上的点与一次函数y=kx+b有什么关系?问题2:以一次函数y=kx+b对应的二元一次方程
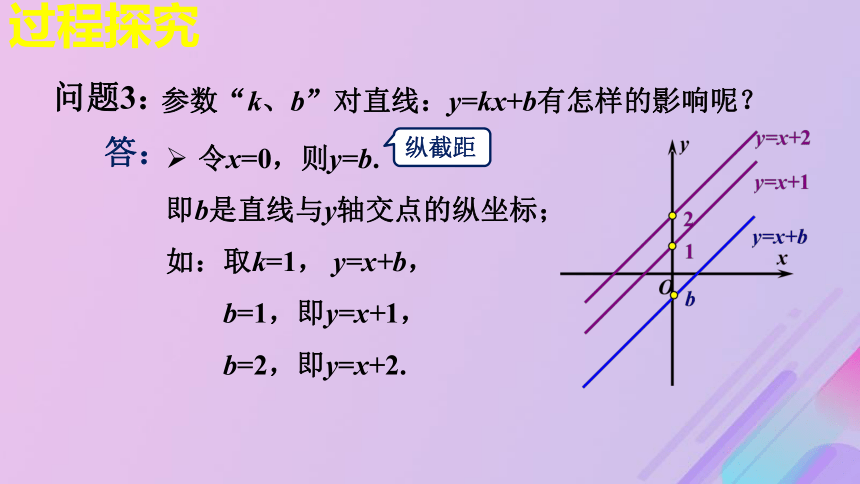
kx+b?y=0的解为坐标的点在直线上.答:过程探究参数“k、b”对直线:y=kx+b有怎样的影响呢?令x=0,则y=b.
即b是直线与y轴交点的纵坐标;
如:取k=1, y=x+b,
b=1,即y=x+1,
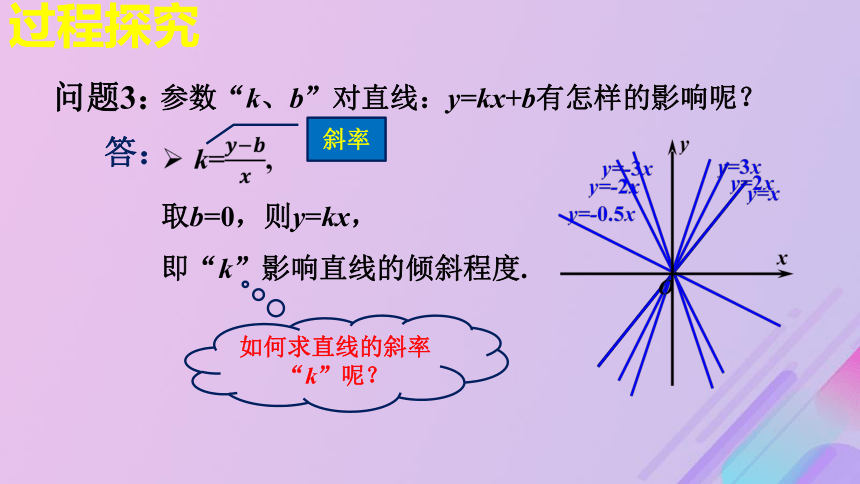
b=2,即y=x+2. 答:纵截距问题3:过程探究?取b=0,则y=kx,
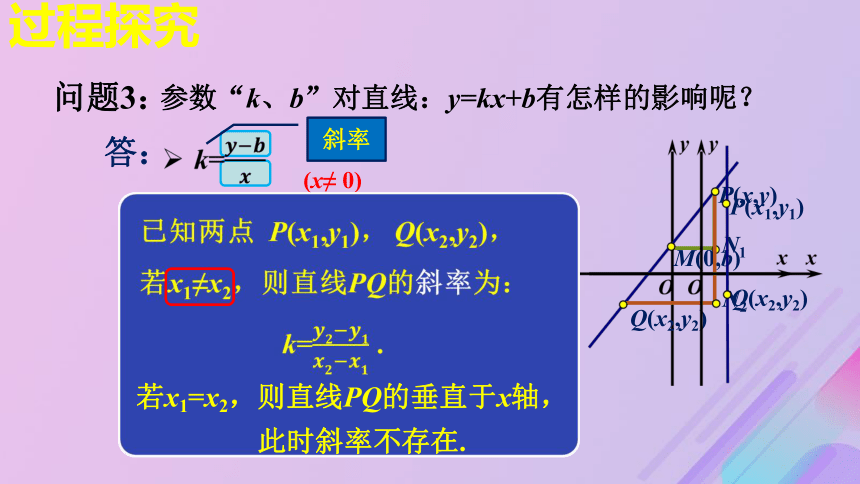
即“k”影响直线的倾斜程度.斜率参数“k、b”对直线:y=kx+b有怎样的影响呢?答:问题3:如何求直线的斜率“k”呢?过程探究M(0,b)N1N2?斜率参数“k、b”对直线:y=kx+b有怎样的影响呢?答:问题3:P(x,y)Q(x2,y2)?(x≠ x2)(x≠ 0)P(x1,y1)Q(x2,y2)纵坐标的增量横坐标的增量若x1=x2,则直线PQ的垂直于x轴,
此时斜率不存在.斜率公式公式的特点:(1)与两点的顺序无关;(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示(3)当x1=x2时,公式不适用,此时直线与x轴垂直思考:斜率的范围是什么?Rl2l1l3过程探究如图,直线l1, l2, l3都经过点P(3, 2),又l1, l2, l3分别经过点Q1(-2, -1), Q2(4, -2), Q3(-3, 2),试计算直线l1, l2, l3的斜率.设直线l1, l2, l3的斜率分别为: k1, k2, k3,
则例1解析:P(3, 2 )Q1(-2, -1)Q2(4, -2)Q3(-3, 2),?直线的斜率可正,可负,还可为零.解后
反思你能从例1中看到当斜率分别是正数,负数,零时,直线的位置有什么特点吗?●●●合作探究(1)当直线的斜率为正值时,直线呈上升趋势( )(2)当直线的斜率为负值时,直线呈下降趋势( )(3)当斜率为0时,直线与 轴平行或重合。( )建构数学直线的倾斜方向与直线斜率关系为:k>0k<0k=0k不存在直线呈上升趋势直线呈下降趋势直线与x轴平行或重合直线垂直于 x轴过程探究k =0k >0k <0斜率不存在?高
度 宽度高
度 宽度倾斜角过程探究 在平面直角坐标系中,对于与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.
规定:与x轴平行或重合的直线的倾斜角为0.倾斜角的定义:①与x轴相交的直线;
②绕交点按逆时针方向旋转;
③最小正角;
④规定:与x轴平行或重合的直线倾斜角为0?;
⑤{? |0?≤?<180?}. 直线的倾斜角和直线的斜率一样,也是刻画直线倾斜程度的量,但直线的倾斜角侧重于直观形象,直线的斜率则侧重于数量关系.
任何直线都有倾斜角,但不是任何直线都有斜率.数学建构直线的倾斜角思考:斜率与倾斜角有
什么关系呢?过程探究k =0k >0k <0斜率不存在Q(x2,y2)P(x1,y1)??N?=tan??=tan??Q(x2,y2)P(x1,y1)N??特别地,??=0? k =0.当直线的斜率为正时,直线的倾斜角为锐角 当直线的倾斜角为α(α≠90°)时: k =tanα我们规定:
1、
2、当α为钝角时: 观察下图,计算l1 ,l2 ,l3 的斜率: (1)(2)当0°<α<90°时, k>0且k随α的增大而增大。 当 90°<α<180 ° 时,k<0且k随α的增大而增大。 当直线的倾斜角为α(α≠90°)时: k=tanα过程探究直线过点P(?3,1),Q(?5,3),求直线PQ的倾斜角??.?例2解析:k=tan??求斜率 例3:已知A、B两点的坐标分别为(-1,1),(2,2),直线l经过点P(0,-2),且直线与线段AB相交,求直线l的斜率的取值范围ABP2-3课堂竞技场数学实践已知三点A(-3,-3),B(-1,1),C(2,7),求KAB,KBCKAB=2KBC=2如果KAB=KBC,那么A、B、C三点有怎样的关系?A、B、C三点共线如果三点A(1,1)、B(3,5)、C(-1,a)在一条直线上,
求a的值(a=-3)小结:
1.斜率;
2.倾斜角.
kx+b?y=0的解为坐标的点在直线上.答:过程探究参数“k、b”对直线:y=kx+b有怎样的影响呢?令x=0,则y=b.
即b是直线与y轴交点的纵坐标;
如:取k=1, y=x+b,
b=1,即y=x+1,
b=2,即y=x+2. 答:纵截距问题3:过程探究?取b=0,则y=kx,
即“k”影响直线的倾斜程度.斜率参数“k、b”对直线:y=kx+b有怎样的影响呢?答:问题3:如何求直线的斜率“k”呢?过程探究M(0,b)N1N2?斜率参数“k、b”对直线:y=kx+b有怎样的影响呢?答:问题3:P(x,y)Q(x2,y2)?(x≠ x2)(x≠ 0)P(x1,y1)Q(x2,y2)纵坐标的增量横坐标的增量若x1=x2,则直线PQ的垂直于x轴,
此时斜率不存在.斜率公式公式的特点:(1)与两点的顺序无关;(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示(3)当x1=x2时,公式不适用,此时直线与x轴垂直思考:斜率的范围是什么?Rl2l1l3过程探究如图,直线l1, l2, l3都经过点P(3, 2),又l1, l2, l3分别经过点Q1(-2, -1), Q2(4, -2), Q3(-3, 2),试计算直线l1, l2, l3的斜率.设直线l1, l2, l3的斜率分别为: k1, k2, k3,
则例1解析:P(3, 2 )Q1(-2, -1)Q2(4, -2)Q3(-3, 2),?直线的斜率可正,可负,还可为零.解后
反思你能从例1中看到当斜率分别是正数,负数,零时,直线的位置有什么特点吗?●●●合作探究(1)当直线的斜率为正值时,直线呈上升趋势( )(2)当直线的斜率为负值时,直线呈下降趋势( )(3)当斜率为0时,直线与 轴平行或重合。( )建构数学直线的倾斜方向与直线斜率关系为:k>0k<0k=0k不存在直线呈上升趋势直线呈下降趋势直线与x轴平行或重合直线垂直于 x轴过程探究k =0k >0k <0斜率不存在?高
度 宽度高
度 宽度倾斜角过程探究 在平面直角坐标系中,对于与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到和直线重合时所转过的最小正角称为这条直线的倾斜角.
规定:与x轴平行或重合的直线的倾斜角为0.倾斜角的定义:①与x轴相交的直线;
②绕交点按逆时针方向旋转;
③最小正角;
④规定:与x轴平行或重合的直线倾斜角为0?;
⑤{? |0?≤?<180?}. 直线的倾斜角和直线的斜率一样,也是刻画直线倾斜程度的量,但直线的倾斜角侧重于直观形象,直线的斜率则侧重于数量关系.
任何直线都有倾斜角,但不是任何直线都有斜率.数学建构直线的倾斜角思考:斜率与倾斜角有
什么关系呢?过程探究k =0k >0k <0斜率不存在Q(x2,y2)P(x1,y1)??N?=tan??=tan??Q(x2,y2)P(x1,y1)N??特别地,??=0? k =0.当直线的斜率为正时,直线的倾斜角为锐角 当直线的倾斜角为α(α≠90°)时: k =tanα我们规定:
1、
2、当α为钝角时: 观察下图,计算l1 ,l2 ,l3 的斜率: (1)(2)当0°<α<90°时, k>0且k随α的增大而增大。 当 90°<α<180 ° 时,k<0且k随α的增大而增大。 当直线的倾斜角为α(α≠90°)时: k=tanα过程探究直线过点P(?3,1),Q(?5,3),求直线PQ的倾斜角??.?例2解析:k=tan??求斜率 例3:已知A、B两点的坐标分别为(-1,1),(2,2),直线l经过点P(0,-2),且直线与线段AB相交,求直线l的斜率的取值范围ABP2-3课堂竞技场数学实践已知三点A(-3,-3),B(-1,1),C(2,7),求KAB,KBCKAB=2KBC=2如果KAB=KBC,那么A、B、C三点有怎样的关系?A、B、C三点共线如果三点A(1,1)、B(3,5)、C(-1,a)在一条直线上,
求a的值(a=-3)小结:
1.斜率;
2.倾斜角.
