2018年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件8苏教版必修2(21张)
文档属性
| 名称 | 2018年高中数学第2章平面解析几何初步2.1.6点到直线的距离课件8苏教版必修2(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 269.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 21:38:07 | ||
图片预览



文档简介
课件21张PPT。点到直线的距离本节导言 本节课研究的问题是
——点到直线的距离如何作出?
——点到直线的垂线段长度
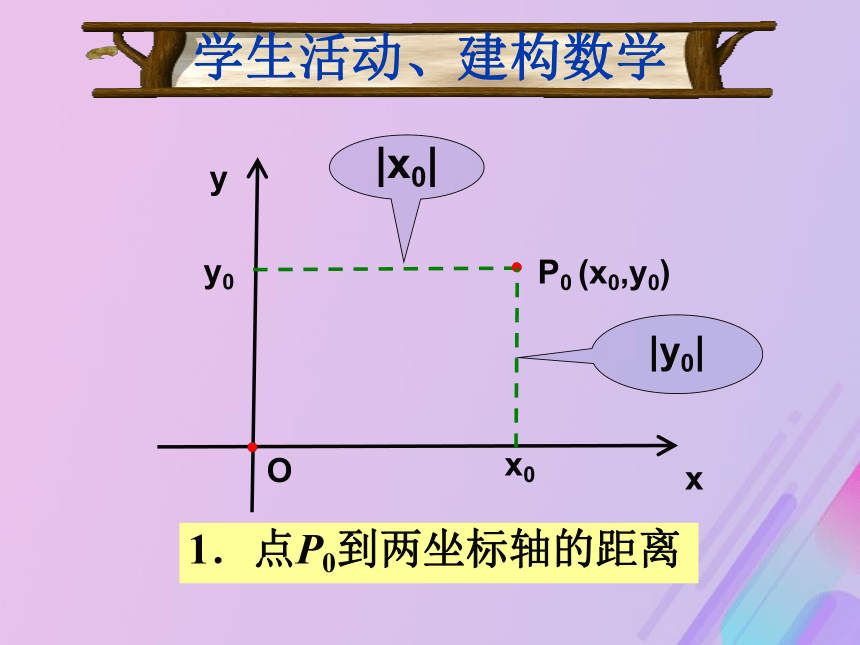
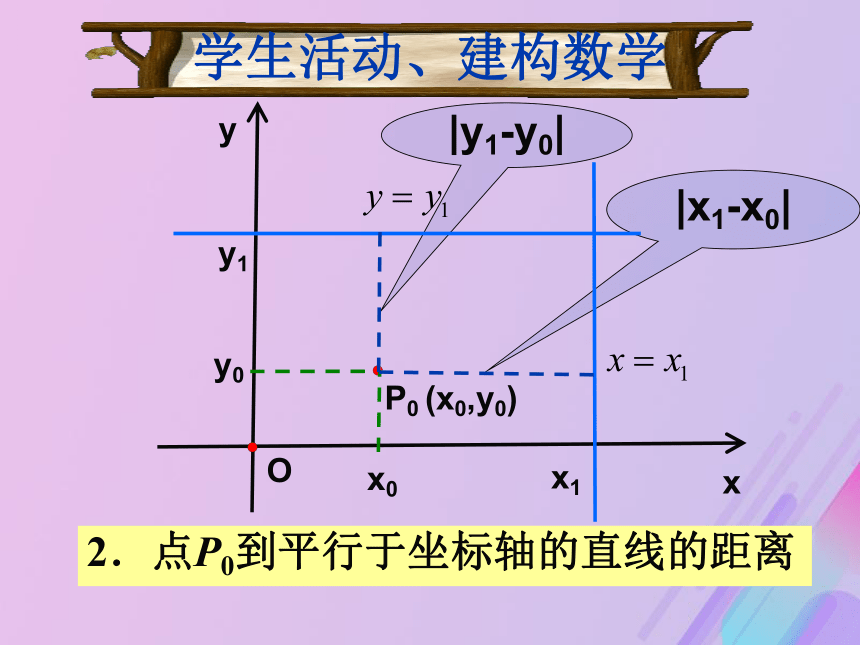
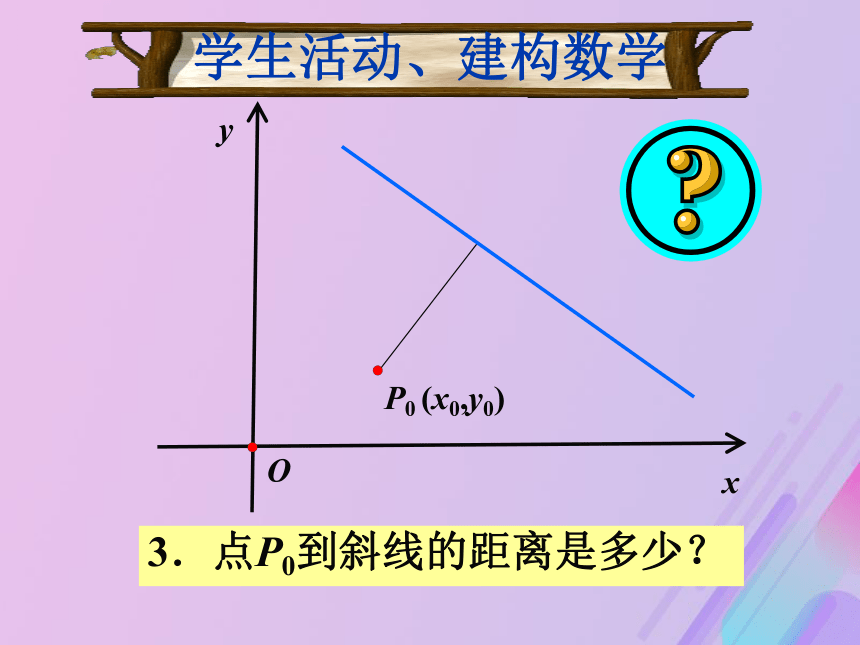
——在坐标平面内,如何用点的坐标和直线的参数来表示点到直线的距离? xyP0 (x0,y0)O|y0||x0|x0y0学生活动、建构数学1.点P0到两坐标轴的距离 xyP0 (x0,y0)O|x1-x0||y1-y0|x0y0y1x1学生活动、建构数学2.点P0到平行于坐标轴的直线的距离 xyP0 (x0,y0)O学生活动、建构数学3.点P0到斜线的距离是多少? 探究:已知平行四边形ABCD的顶点坐标为A(?1,3),B(3,?2),C(6,?1),D(2,4),如何计算它的面积?
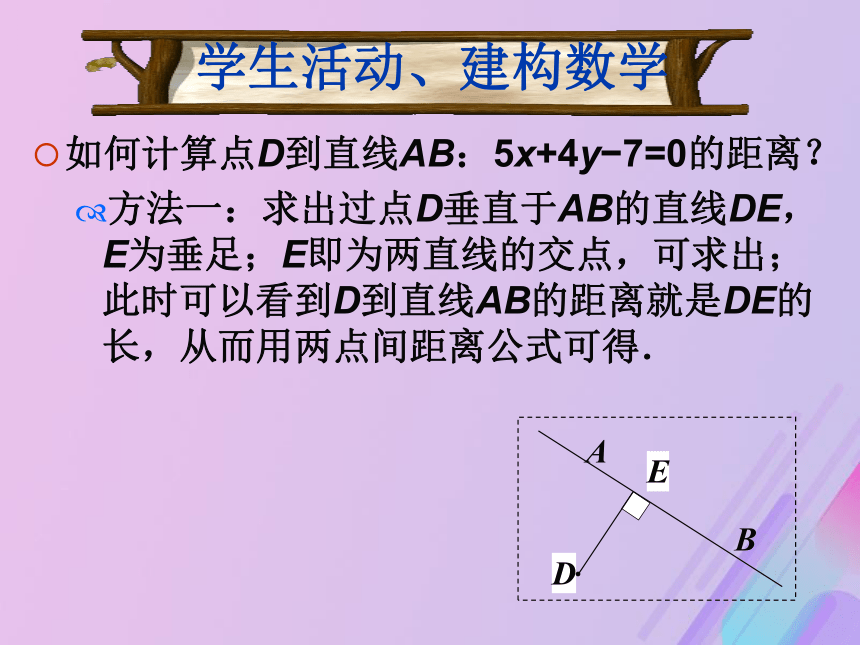
在前面我们已经研究过两点间的距离公式,所以能够求出平行四边形的一边长来,但是现在的问题是我们还需要求出这边上的高,即点到直线的距离. 问题情境 学生活动、建构数学如何计算点D到直线AB:5x+4y?7=0的距离?
方法一:求出过点D垂直于AB的直线DE,E为垂足;E即为两直线的交点,可求出;此时可以看到D到直线AB的距离就是DE的长,从而用两点间距离公式可得. ED学生活动、建构数学如何计算点D到直线AB:5x+4y?7=0的距离?
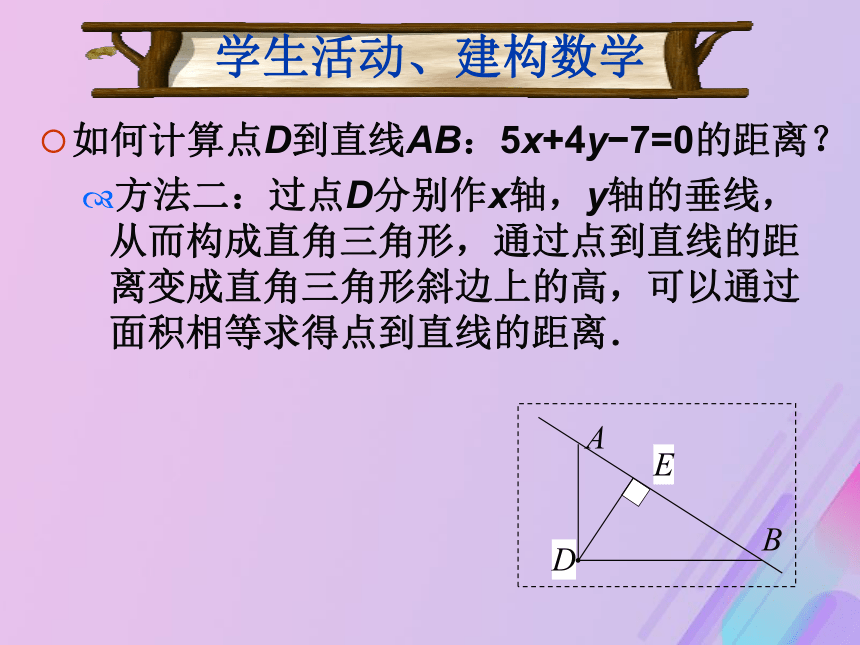
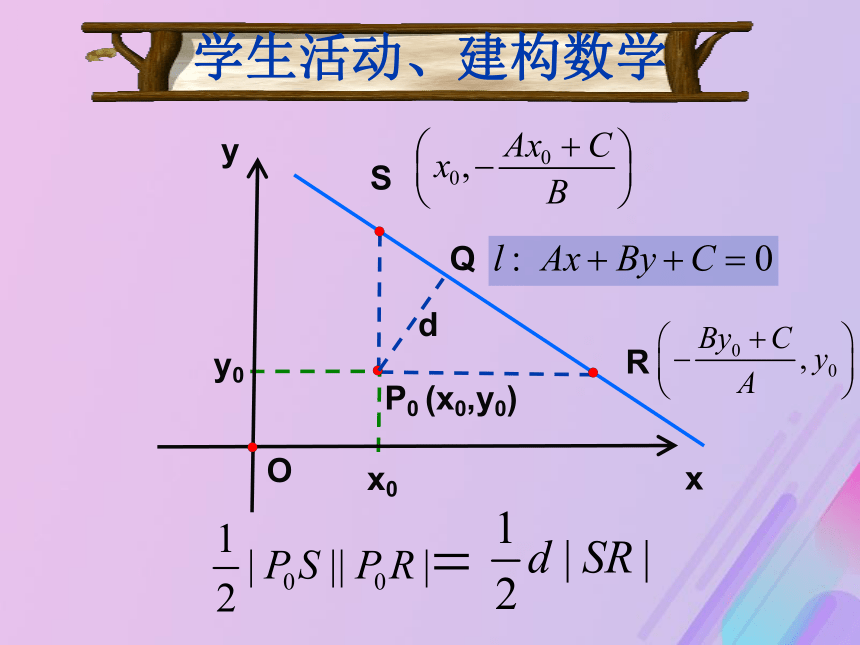
方法二:过点D分别作x轴,y轴的垂线,从而构成直角三角形,通过点到直线的距离变成直角三角形斜边上的高,可以通过面积相等求得点到直线的距离. ABEDxyP0 (x0,y0)Ox0y0SRQd学生活动、建构数学xyP0 (x0,y0)OSRQd数学理论数学运用(例1)求点P(?1,2)到下列直线的距离:
(1)2x+y?10=0;
(2)3x=2. 数学运用(课内练习)
1.若点(4, 0)到直线4x-3y+a=0的距离为3,则a的取值为________.
2. 动点P在直线x+y-4=0上,O为原点,则OP的最小值为_______.
3. 点P在直线3x+y-5=0上,点P到直线x-y-1=0的距离为,则点P的坐标是______________. 数学运用(例2)求两条平行线x+3y?4=0与2x+6y?9=0之间的距离. 数学运用(思考)一般地,已知两条平行直线 l1:Ax+By+C1=0,l2:Ax+By+C2=0(C1≠C2) 怎样求直线l1和l2之间的距离? 数学理论一般地,已知两条平行直线 l1:Ax+By+C1=0,l2:Ax+By+C2=0(C1≠C2) 怎样求直线l1和l2之间的距离?
记两直线间的距离为d,则数学运用(练习)记两直线间的距离为d,则
下列平行线间的距离是多少?
(1)2x?y=0,2x?y+5=0;
(2)x+2y?3=0,2x+4y?5=0.
数学运用(例3)建立适当的直角坐标系, 证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.
(1)课本P93 练习1;
(2)课本P93 练习2. 数学运用(课内练习)回顾反思
两条直线平行的等价条件是什么?
——斜率相等.课后作业
课本P84练习
1.(1)(3); 5.; 10.(1)谢谢合作!
——点到直线的距离如何作出?
——点到直线的垂线段长度
——在坐标平面内,如何用点的坐标和直线的参数来表示点到直线的距离? xyP0 (x0,y0)O|y0||x0|x0y0学生活动、建构数学1.点P0到两坐标轴的距离 xyP0 (x0,y0)O|x1-x0||y1-y0|x0y0y1x1学生活动、建构数学2.点P0到平行于坐标轴的直线的距离 xyP0 (x0,y0)O学生活动、建构数学3.点P0到斜线的距离是多少? 探究:已知平行四边形ABCD的顶点坐标为A(?1,3),B(3,?2),C(6,?1),D(2,4),如何计算它的面积?
在前面我们已经研究过两点间的距离公式,所以能够求出平行四边形的一边长来,但是现在的问题是我们还需要求出这边上的高,即点到直线的距离. 问题情境 学生活动、建构数学如何计算点D到直线AB:5x+4y?7=0的距离?
方法一:求出过点D垂直于AB的直线DE,E为垂足;E即为两直线的交点,可求出;此时可以看到D到直线AB的距离就是DE的长,从而用两点间距离公式可得. ED学生活动、建构数学如何计算点D到直线AB:5x+4y?7=0的距离?
方法二:过点D分别作x轴,y轴的垂线,从而构成直角三角形,通过点到直线的距离变成直角三角形斜边上的高,可以通过面积相等求得点到直线的距离. ABEDxyP0 (x0,y0)Ox0y0SRQd学生活动、建构数学xyP0 (x0,y0)OSRQd数学理论数学运用(例1)求点P(?1,2)到下列直线的距离:
(1)2x+y?10=0;
(2)3x=2. 数学运用(课内练习)
1.若点(4, 0)到直线4x-3y+a=0的距离为3,则a的取值为________.
2. 动点P在直线x+y-4=0上,O为原点,则OP的最小值为_______.
3. 点P在直线3x+y-5=0上,点P到直线x-y-1=0的距离为,则点P的坐标是______________. 数学运用(例2)求两条平行线x+3y?4=0与2x+6y?9=0之间的距离. 数学运用(思考)一般地,已知两条平行直线 l1:Ax+By+C1=0,l2:Ax+By+C2=0(C1≠C2) 怎样求直线l1和l2之间的距离? 数学理论一般地,已知两条平行直线 l1:Ax+By+C1=0,l2:Ax+By+C2=0(C1≠C2) 怎样求直线l1和l2之间的距离?
记两直线间的距离为d,则数学运用(练习)记两直线间的距离为d,则
下列平行线间的距离是多少?
(1)2x?y=0,2x?y+5=0;
(2)x+2y?3=0,2x+4y?5=0.
数学运用(例3)建立适当的直角坐标系, 证明:等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高.
(1)课本P93 练习1;
(2)课本P93 练习2. 数学运用(课内练习)回顾反思
两条直线平行的等价条件是什么?
——斜率相等.课后作业
课本P84练习
1.(1)(3); 5.; 10.(1)谢谢合作!
