2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(18张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.1利用导数判断函数的单调性课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 21:28:55 | ||
图片预览





文档简介
课件18张PPT。利用导数判断函数的单调性 ★ 创设情境 ★ 创设情境如何判断函数的单调性呢?★
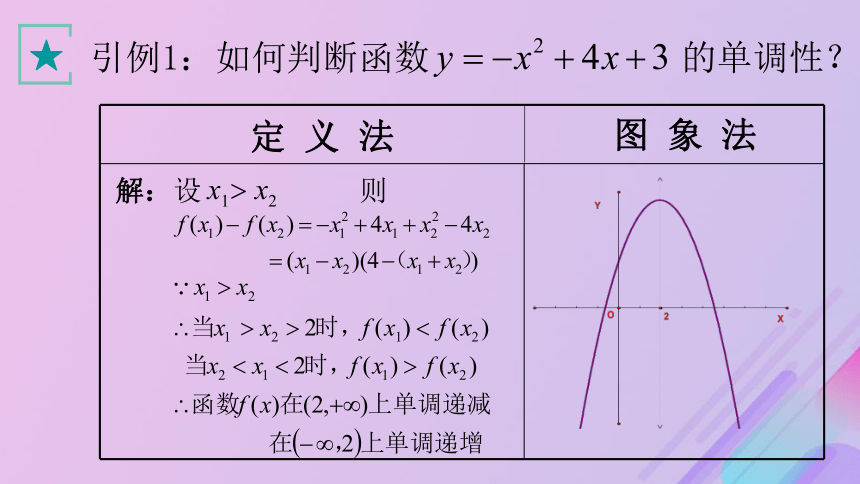
引例1:如何判断函数 的单调性?
解:设 则 定 义 法 图 象 法 ★
引例2:如何判断函数 的单调性?
小组讨论利用导数判断函数的单调性学习目标借助于函数的图象了解函数的单调性与导数的关系会判断具体函数在给定区间上的单调性;会求具体函数的单调区间.培养学生的观察能力、归纳能力,增强数形结合的思维意识. ★ 新课引入1.在x=1的左侧函数图象呈现什么趋势?3.结合导数的几何意义,你可以得到什么结论?4.在x=1的右边时,同时回答上述问题2.在x=1的左侧函数图象上的各点切线的倾斜角为 (锐角/钝角)?他的斜率有什么特征?下降K<0f'(x)<0 ★ 探求新知在(-∞,0)上:K<0,即f'(x)<0,单调递减
在(0,+∞)上:K<0,即f'(x)<0,单调递减
函数的单调性和导数有什么关系呢? ★ 获取新知 利用导数判断函数单调性的法则: ★ 获取新知
1.如果在 内, ,则 在此区间是增函数,
为 的单调递增区间
2.如果在 内, ,则 在此区间是减函数,
为 的单调递减区间利用导数判断函数单调性的法则:★
引例2:如何判断函数 的单调性?
★ 尝试练习 求函数 的单调区间 ★ 归纳总结利用导数判断函数单调性的步骤是什么?
(1)求函数的定义域
(2)求函数的导数
(3)令f'(x)>0以及f'(x)<0,求自变量x的取值
范围,即函数的单调区间★ 本课小结 ★ 当堂检测1、确定函数 的单调性 2、 的单调减区间为( )A . B. 和
C . D.增区间: 减区间: A ★ 作业1.必做题:课本P27 A 2题 B 3题 2. 探究题:判断函数 在区间
的单调性谢 谢
引例1:如何判断函数 的单调性?
解:设 则 定 义 法 图 象 法 ★
引例2:如何判断函数 的单调性?
小组讨论利用导数判断函数的单调性学习目标借助于函数的图象了解函数的单调性与导数的关系会判断具体函数在给定区间上的单调性;会求具体函数的单调区间.培养学生的观察能力、归纳能力,增强数形结合的思维意识. ★ 新课引入1.在x=1的左侧函数图象呈现什么趋势?3.结合导数的几何意义,你可以得到什么结论?4.在x=1的右边时,同时回答上述问题2.在x=1的左侧函数图象上的各点切线的倾斜角为 (锐角/钝角)?他的斜率有什么特征?下降K<0f'(x)<0 ★ 探求新知在(-∞,0)上:K<0,即f'(x)<0,单调递减
在(0,+∞)上:K<0,即f'(x)<0,单调递减
函数的单调性和导数有什么关系呢? ★ 获取新知 利用导数判断函数单调性的法则: ★ 获取新知
1.如果在 内, ,则 在此区间是增函数,
为 的单调递增区间
2.如果在 内, ,则 在此区间是减函数,
为 的单调递减区间利用导数判断函数单调性的法则:★
引例2:如何判断函数 的单调性?
★ 尝试练习 求函数 的单调区间 ★ 归纳总结利用导数判断函数单调性的步骤是什么?
(1)求函数的定义域
(2)求函数的导数
(3)令f'(x)>0以及f'(x)<0,求自变量x的取值
范围,即函数的单调区间★ 本课小结 ★ 当堂检测1、确定函数 的单调性 2、 的单调减区间为( )A . B. 和
C . D.增区间: 减区间: A ★ 作业1.必做题:课本P27 A 2题 B 3题 2. 探究题:判断函数 在区间
的单调性谢 谢
