2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(20张)
文档属性
| 名称 | 2018年高中数学新人教B版选修1-1课件:第三章导数及其应用3.3.2利用导数研究函数的极值课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 547.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览








文档简介
课件20张PPT。3.3.2 函数的极值与导数冲浪运动模拟:在某个区间(a,b)内,
如果f ?(x)>0,那么函数y=f (x)在这个区间内________;
如果f ?(x)<0,那么函数y=f (x)在这个区间内________.单调递增单调递减温故而知新函数的导数和函数单调性的关系是什么?(1)当t=a时,h 最大,那么h?(a)是多少?(2)此点附近的图象有什么特点?(3)导数的符号有什么变化规律?观察跳水运动中高度随时间变化的函数图像,回答问题:t>at0单调递增单调递减h?(a)=0思考3.3.2 函数的极值与导数 (3)在点 a 附近, y=f(x)的导数的符号有什么规律?
(1)函数y=f(x) 在 a 点的函数值与它附近的函数值有什么关系?(2)函数y=f(x) 在 a 点的的导数值是多少? (图一)问题:bbb-+00+-极值的概念(1)函数y=f(x) 在点x=a的函数值比它附近的函数值都小,f′(a)=0;且在点x=a附近的左侧f′(a)<0,右侧f′(a) >0极值的定义:(2)函数y=f(x) 在点x=b的函数值比它附近的函数值都大,f′(b)=0;且在点x=b附近的左侧f′(b)>0,右侧f′(b)<0
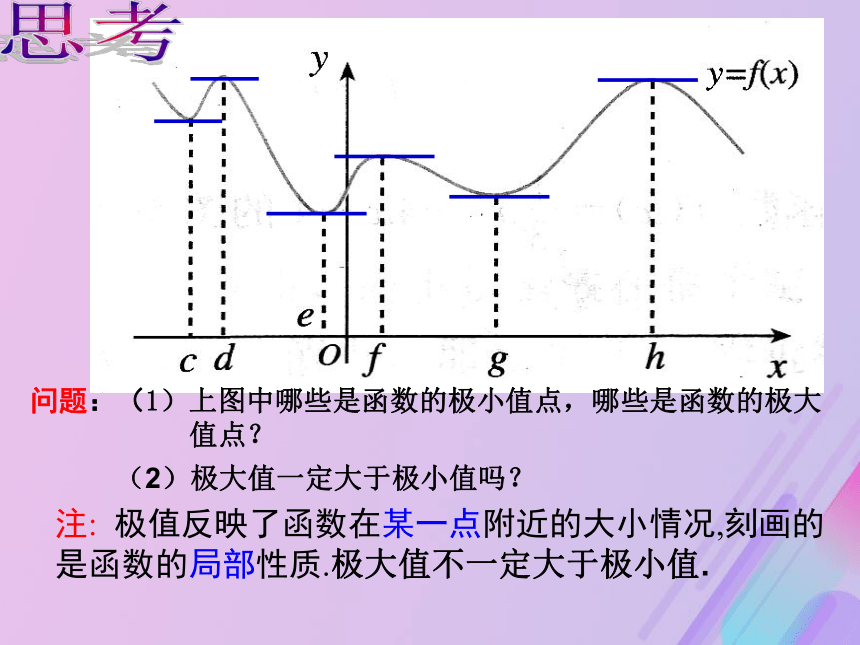
我们把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.请你在归纳上述问题的基础上,给出函数极值的概念我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.极小值点、极大值点统称极值点,极大值和极小值统称为极值.注: 极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性质.极大值不一定大于极小值.
问题:(1)上图中哪些是函数的极小值点,哪些是函数的极大
值点?(2)极大值一定大于极小值吗?思考解方程f ?(x)=0.(1)如果在x0附近的左侧f ?(x)>0,右侧f ?(x)<0,那么f (x0)是极大值;(2)如果在x0附近的左侧f ?(x)<0,右侧f ?(x)>0,那么f (x0)是极小值.1、如何求函数的极值点?2、若函数y=f(x)在xo处取得极值,如何知道xo是极大值点还是极小值点?求函数极值的方法当f ?(x0)=0时
如图是导函数 的图象,试找出函数 的极值点,并指出哪些是极大值点,哪些是极小值点?答:x2,x4是函数y=f(x)的极值点,其中x2是函数y=f(x)的极大值点,x4是函数y=f(x)的极小值点。1、函数在极值点处的导数值有什么特征? 2、导数值为0的点是否一定是极值点? 函数在一点的导数值为0是其在这点取极值的 条件.思考f’(0)=0必要条件,而非充分例1求函数f(x)极值的步骤:(2)求导数f '(x);(3)求方程f ’(x)=0的根; (4)把定义域划分为部分区间,并列成表格检查f ’(x)在方程根左右的符号——
如果左正右负(+ ~ -),
那么f(x)在这个根处取得极大值如果左负右正(- ~ +),
那么f(x)在这个根处取得极小值;(1) 确定函数的定义域;跟踪训练求下列函数的极值2、求极值的步骤:
(1)确定函数的定义域
(2)求导数f'(x)
(3)求方程f'(x) =0的全部解
(4)检查f'(x)在f'(x) =0的根左.右两边值的符号,如果左正右负
(或左负右正),那么f(x)在这个根取得极大值或极小值
1、函数的极值课堂小结2. 求函数f(x)=6-12x+x3的极值:1、如图是y=f(x)导函数y=f′(x)的图象,在标记的点中,在哪一点处
(1)导函数y=f′(x)有极大值?
(2)导函数y=f′(x)有极小值?
(3)函数y=f(x)有极大值?
(4)函数y=f(x)有极小值?
自我检测x1,x4x3x2x5因此当x=-2时,f(x)有极大值,并且极大值为22;
当x=2时,f(x)有极小值,并且极小值为-10.
解:∵f(x)=6-12x+x3(x∈R)∴f′(x)=-12+3x2令f′(x)=0, 得x=2,或x=-2.列表如下:本节内容结束例1解得x=2, 或 x=-2.讨论:(1)当f ?(x)>0,即x>2,或x<-2时;
(2)当f ?(x)<0,即-2
如果f ?(x)>0,那么函数y=f (x)在这个区间内________;
如果f ?(x)<0,那么函数y=f (x)在这个区间内________.单调递增单调递减温故而知新函数的导数和函数单调性的关系是什么?(1)当t=a时,h 最大,那么h?(a)是多少?(2)此点附近的图象有什么特点?(3)导数的符号有什么变化规律?观察跳水运动中高度随时间变化的函数图像,回答问题:t>at
(1)函数y=f(x) 在 a 点的函数值与它附近的函数值有什么关系?(2)函数y=f(x) 在 a 点的的导数值是多少? (图一)问题:bbb-+00+-极值的概念(1)函数y=f(x) 在点x=a的函数值比它附近的函数值都小,f′(a)=0;且在点x=a附近的左侧f′(a)<0,右侧f′(a) >0极值的定义:(2)函数y=f(x) 在点x=b的函数值比它附近的函数值都大,f′(b)=0;且在点x=b附近的左侧f′(b)>0,右侧f′(b)<0
我们把点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.请你在归纳上述问题的基础上,给出函数极值的概念我们把点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.极小值点、极大值点统称极值点,极大值和极小值统称为极值.注: 极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性质.极大值不一定大于极小值.
问题:(1)上图中哪些是函数的极小值点,哪些是函数的极大
值点?(2)极大值一定大于极小值吗?思考解方程f ?(x)=0.(1)如果在x0附近的左侧f ?(x)>0,右侧f ?(x)<0,那么f (x0)是极大值;(2)如果在x0附近的左侧f ?(x)<0,右侧f ?(x)>0,那么f (x0)是极小值.1、如何求函数的极值点?2、若函数y=f(x)在xo处取得极值,如何知道xo是极大值点还是极小值点?求函数极值的方法当f ?(x0)=0时
如图是导函数 的图象,试找出函数 的极值点,并指出哪些是极大值点,哪些是极小值点?答:x2,x4是函数y=f(x)的极值点,其中x2是函数y=f(x)的极大值点,x4是函数y=f(x)的极小值点。1、函数在极值点处的导数值有什么特征? 2、导数值为0的点是否一定是极值点? 函数在一点的导数值为0是其在这点取极值的 条件.思考f’(0)=0必要条件,而非充分例1求函数f(x)极值的步骤:(2)求导数f '(x);(3)求方程f ’(x)=0的根; (4)把定义域划分为部分区间,并列成表格检查f ’(x)在方程根左右的符号——
如果左正右负(+ ~ -),
那么f(x)在这个根处取得极大值如果左负右正(- ~ +),
那么f(x)在这个根处取得极小值;(1) 确定函数的定义域;跟踪训练求下列函数的极值2、求极值的步骤:
(1)确定函数的定义域
(2)求导数f'(x)
(3)求方程f'(x) =0的全部解
(4)检查f'(x)在f'(x) =0的根左.右两边值的符号,如果左正右负
(或左负右正),那么f(x)在这个根取得极大值或极小值
1、函数的极值课堂小结2. 求函数f(x)=6-12x+x3的极值:1、如图是y=f(x)导函数y=f′(x)的图象,在标记的点中,在哪一点处
(1)导函数y=f′(x)有极大值?
(2)导函数y=f′(x)有极小值?
(3)函数y=f(x)有极大值?
(4)函数y=f(x)有极小值?
自我检测x1,x4x3x2x5因此当x=-2时,f(x)有极大值,并且极大值为22;
当x=2时,f(x)有极小值,并且极小值为-10.
解:∵f(x)=6-12x+x3(x∈R)∴f′(x)=-12+3x2令f′(x)=0, 得x=2,或x=-2.列表如下:本节内容结束例1解得x=2, 或 x=-2.讨论:(1)当f ?(x)>0,即x>2,或x<-2时;
(2)当f ?(x)<0,即-2
