2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件3新人教B版选修2_1(19张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.2.2椭圆的几何性质课件3新人教B版选修2_1(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 558.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览



文档简介
课件19张PPT。椭圆的简单几何性质(1)12复习回顾:1.椭圆的定义:平面内与两定点F1、F2的距离和等于常数(大于|F1F2 |)的点的轨迹叫做椭圆.2.椭圆的标准方程是:3.椭圆中a,b,c的关系是:3新知探究:椭圆的简单几何性质4一、椭圆的范围:
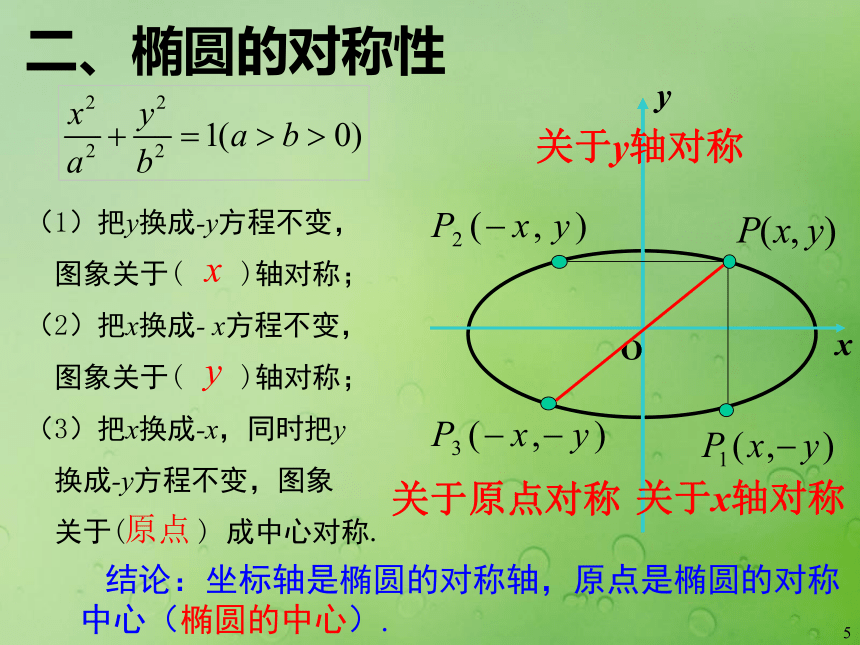
结论:椭圆落在直线 围成的矩形框中 椭圆 的简单几何性质x新知探究:5关于x轴对称关于y轴对称关于原点对称二、椭圆的对称性(1)把y换成-y方程不变,
图象关于( )轴对称;
(2)把x换成- x方程不变,
图象关于( )轴对称;
(3)把x换成-x,同时把y
换成-y方程不变,图象
关于( ) 成中心对称.
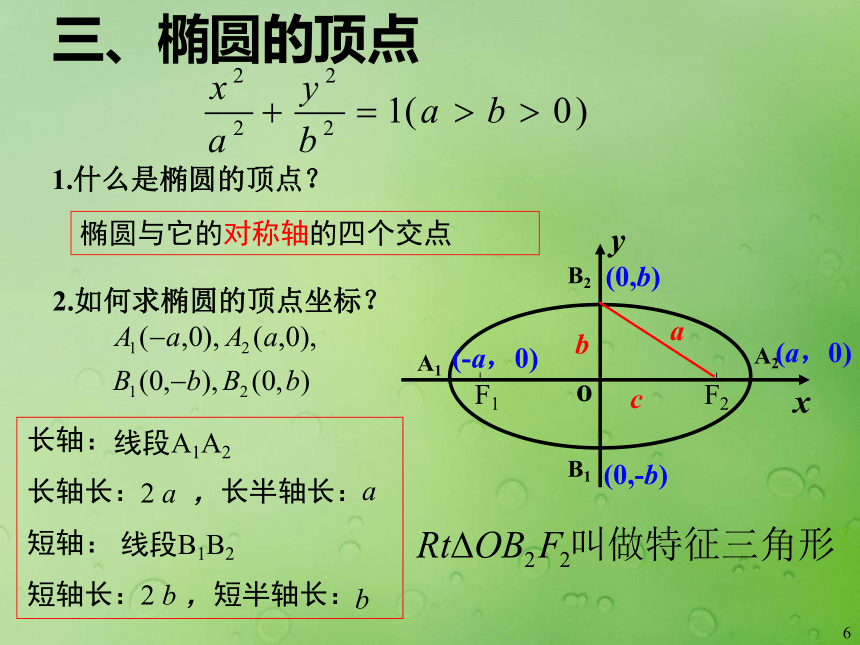
xy原点 结论:坐标轴是椭圆的对称轴,原点是椭圆的对称中心(椭圆的中心).6三、椭圆的顶点1.什么是椭圆的顶点?长轴:
长轴长: ,长半轴长:
短轴:
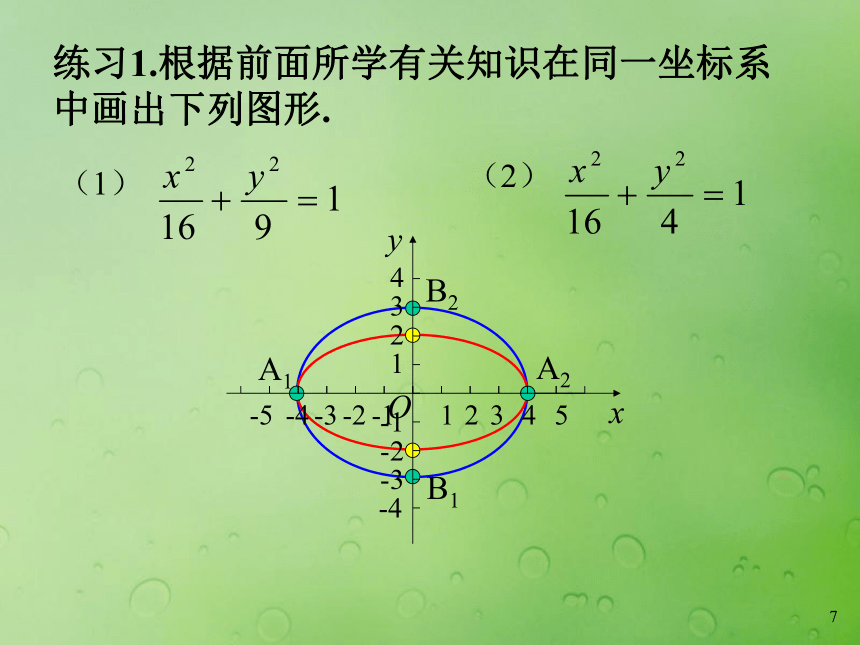
短轴长: ,短半轴长:x椭圆与它的对称轴的四个交点2.如何求椭圆的顶点坐标?bca线段A1A22 a线段B1B22 bba7练习1.根据前面所学有关知识在同一坐标系
中画出下列图形.(1)(2)A1 B1 A2 B2 问题1:椭圆有些比较“扁”,有些比较“圆”,
用什么刻画椭圆“扁”的程度呢?8a保持不变时, b就越小,此时椭圆就越扁b就越大,此时椭圆就越圆9问题2:能用 的大小刻画椭圆的扁平程度吗?a(合作探究)10四、椭圆的离心率x刻画椭圆扁平程度的量2.为什么定义 为离心率呢?1.什么是离心率?11[1]离心率的取值范围:[2]离心率对椭圆形状的影响: 此时椭圆就越扁 2)e 越接近 0,c 就越接近 0,此时椭圆就越圆结论:离心率越大,椭圆越扁;离心率越小,椭圆越圆.因为 a > c > 0,所以0 < e < 1
1)e 越接近 1,c 就越接近 a,
12关于x轴、y轴成轴对称;
关于原点成中心对称.长半轴长为a,
短半轴长为b焦距为2c关于x轴、y轴成轴对称;
关于原点成中心对称.长半轴长为a,
短半轴长为b焦距为2c
关于x轴、y轴成轴对称;关于原点成中心对称.
长半轴长为a,短半轴长为b
.
焦距为2c
13 例1.已知椭圆方程为分析:椭圆方程转化为标准方程为:
a=5 b=4 c=3108614求椭圆的标准方程时, 应: 先定位(焦点), 再定量(a、b) 变式:若椭圆方程为15知识巩固:例2.中心在原点,焦点在坐标轴上,离心率
为 且过(2,0),求椭圆的标准方程 .16当焦点位置不确定时,要讨论,此时有两个解!(2)已知点P在以坐标轴为对称轴的椭圆上, 点P 到两焦点的距离分别为 和 ,过P 作长轴的垂线恰好经过椭圆的一个焦点.求椭圆的标准方程时, 应: 先定位(焦点), 再定量(a、b)小结:1.椭圆的基本要素:172.数学思想方法:
(1)基本量:a、b、c、e(共四个量)(2)基本点:顶点、焦点、中心(共七个点)(3)基本线:对称轴(共两条线)(1)数与形的结合,用代数的方法解决几何问题;
(2)分类讨论的数学思想 .
{1}基本量:a、b、c、e、(共四个量){2}基本点:顶点、焦点、中心(共七个点){3}基本线:对称轴(共两条线)请考虑:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)F1F2椭圆的基本要素:18191.椭圆以坐标轴为对称轴,离心率 ,长轴长为6,则椭圆的方程 为( )C目标测试: 2. 若椭圆的一个焦点与短轴的
两端点构成一个正三角形, 则
椭圆的离心率 e =_____.
结论:椭圆落在直线 围成的矩形框中 椭圆 的简单几何性质x新知探究:5关于x轴对称关于y轴对称关于原点对称二、椭圆的对称性(1)把y换成-y方程不变,
图象关于( )轴对称;
(2)把x换成- x方程不变,
图象关于( )轴对称;
(3)把x换成-x,同时把y
换成-y方程不变,图象
关于( ) 成中心对称.
xy原点 结论:坐标轴是椭圆的对称轴,原点是椭圆的对称中心(椭圆的中心).6三、椭圆的顶点1.什么是椭圆的顶点?长轴:
长轴长: ,长半轴长:
短轴:
短轴长: ,短半轴长:x椭圆与它的对称轴的四个交点2.如何求椭圆的顶点坐标?bca线段A1A22 a线段B1B22 bba7练习1.根据前面所学有关知识在同一坐标系
中画出下列图形.(1)(2)A1 B1 A2 B2 问题1:椭圆有些比较“扁”,有些比较“圆”,
用什么刻画椭圆“扁”的程度呢?8a保持不变时, b就越小,此时椭圆就越扁b就越大,此时椭圆就越圆9问题2:能用 的大小刻画椭圆的扁平程度吗?a(合作探究)10四、椭圆的离心率x刻画椭圆扁平程度的量2.为什么定义 为离心率呢?1.什么是离心率?11[1]离心率的取值范围:[2]离心率对椭圆形状的影响: 此时椭圆就越扁 2)e 越接近 0,c 就越接近 0,此时椭圆就越圆结论:离心率越大,椭圆越扁;离心率越小,椭圆越圆.因为 a > c > 0,所以0 < e < 1
1)e 越接近 1,c 就越接近 a,
12关于x轴、y轴成轴对称;
关于原点成中心对称.长半轴长为a,
短半轴长为b焦距为2c关于x轴、y轴成轴对称;
关于原点成中心对称.长半轴长为a,
短半轴长为b焦距为2c
关于x轴、y轴成轴对称;关于原点成中心对称.
长半轴长为a,短半轴长为b
.
焦距为2c
13 例1.已知椭圆方程为分析:椭圆方程转化为标准方程为:
a=5 b=4 c=3108614求椭圆的标准方程时, 应: 先定位(焦点), 再定量(a、b) 变式:若椭圆方程为15知识巩固:例2.中心在原点,焦点在坐标轴上,离心率
为 且过(2,0),求椭圆的标准方程 .16当焦点位置不确定时,要讨论,此时有两个解!(2)已知点P在以坐标轴为对称轴的椭圆上, 点P 到两焦点的距离分别为 和 ,过P 作长轴的垂线恰好经过椭圆的一个焦点.求椭圆的标准方程时, 应: 先定位(焦点), 再定量(a、b)小结:1.椭圆的基本要素:172.数学思想方法:
(1)基本量:a、b、c、e(共四个量)(2)基本点:顶点、焦点、中心(共七个点)(3)基本线:对称轴(共两条线)(1)数与形的结合,用代数的方法解决几何问题;
(2)分类讨论的数学思想 .
{1}基本量:a、b、c、e、(共四个量){2}基本点:顶点、焦点、中心(共七个点){3}基本线:对称轴(共两条线)请考虑:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)F1F2椭圆的基本要素:18191.椭圆以坐标轴为对称轴,离心率 ,长轴长为6,则椭圆的方程 为( )C目标测试: 2. 若椭圆的一个焦点与短轴的
两端点构成一个正三角形, 则
椭圆的离心率 e =_____.
