2018年高中数学第二章圆锥曲线与方程2.3.1双曲线的标准方程课件3新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.3.1双曲线的标准方程课件3新人教B版选修2_1(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 811.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:30:59 | ||
图片预览





文档简介
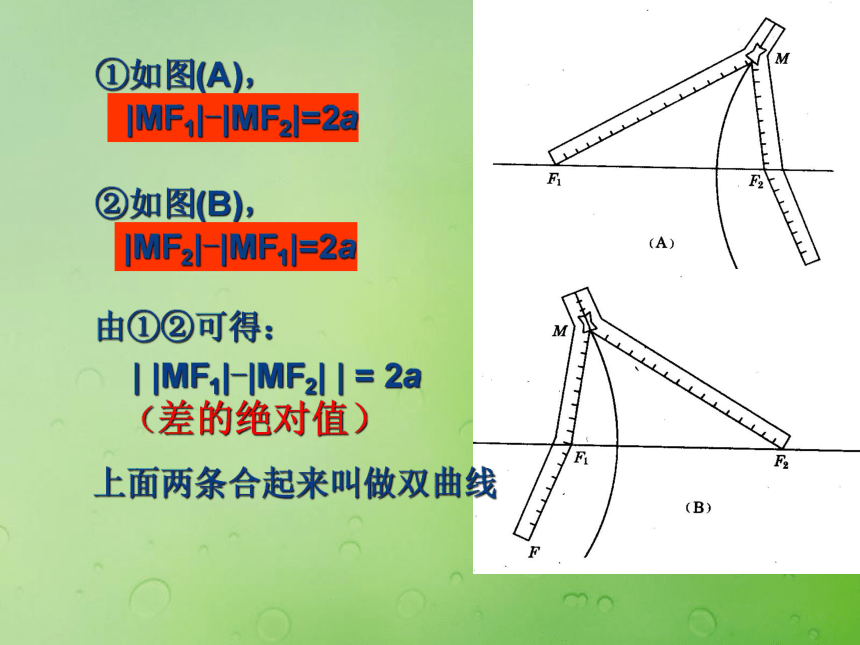
课件14张PPT。2.3.1 双曲线的标准方程问题1:椭圆的定义是什么?平面内与两个定点F1F2的距离的和等于常数(大于|F1F2| )的点的轨迹叫做椭圆。问题2:椭圆的标准方程是怎样的? , , 关系如何?问题3:如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?复习引入①如图(A), |MF1|-|MF2|=2a②如图(B),|MF2|-|MF1|=2a上面两条合起来叫做双曲线由①②可得: | |MF1|-|MF2| | = 2a
(差的绝对值)平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|,且不等于0)的点的轨迹叫做双曲线。这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距。通常情况下,我们把|F1F2|记为2c(c>0); 常数记为2a(a>0).问题2:
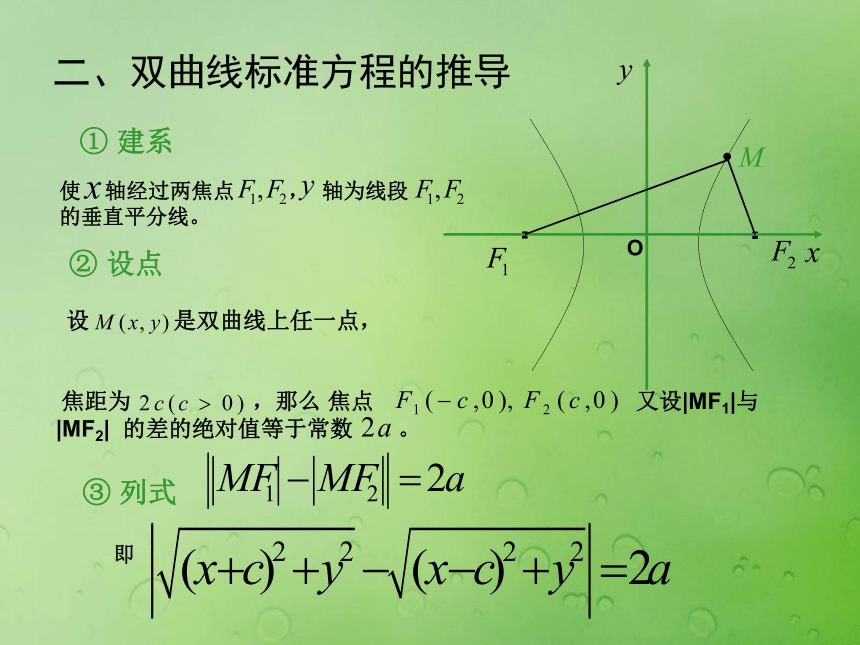
定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?问题1:定义中为什么强调距离差的绝对值为常数?一、双曲线的定义①若2a=2c,则轨迹是什么?②若2a>2c,则轨迹是什么?③若2a=0,则轨迹是什么?此时轨迹为以F1或F2为端点的两条射线此时轨迹不存在此时轨迹为线段F1F2的垂直平分线F1F2F1F2分3种情况来看:二、双曲线标准方程的推导① 建系使 轴经过两焦点 , 轴为线段 的垂直平分线。② 设点设 是双曲线上任一点, 焦距为 ,那么 焦点 又设|MF1|与|MF2| 的差的绝对值等于常数 。③ 列式即将上述方程化为: 移项两边平方后整理得: 两边再平方后整理得: 由双曲线定义知: 即:设 代入上式整理得: 两边同时除以 得:④化简这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在x轴上,焦点是 F1(-c,0),F2(c,0).其中c2=a2+b2.类比椭圆的标准方程,请思考焦点在y轴上的双曲线的标准方程是什么?其中c2=a2+b2.这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在y轴上,焦点是 F1(0,-c),F2(0,c).三.双曲线两种标准方程的比较① 方程用“-”号连接。② 分母是 但 大小不定。③ 。 ④如果 的系数是正的,则焦点在 轴上;如果 的系数是正的,则焦点在 轴上。F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2四、双曲线与椭圆之间的区别与联系||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)例题解:因为双曲线的焦点在x轴上,所以设它的标准方程为因此,双曲线的标准方程为方法总结:
求标准方程要做到先定型,后定量。两条射线轨迹不存在例1、已知双曲线的焦点 F1(-5,0), F2(5,0),双曲线上一点P到焦点的距离差的绝对值等于8,求双曲线的标准方程。1.若|PF1|-|PF2|=8呢?2.若||PF1|-|PF2||=10呢?3.若||PF1|-|PF2||=12呢?所以2c=10,2a=8。即a=4,c=5那么b2=c2-a2=25-16=9根据已知条件,|F1F2|=10. ||PF1|-|PF2||=8,归纳小结双曲线的定义双曲线的标准方程布置作业
54页习题2.2 A组1、2题。谢谢!题后反思(1)先把非标准方程化成标准方程,再判断焦点所在的坐标轴。(2) 是否表示双曲线? 表示焦点在 轴上的双曲线;表示焦点在 轴上的双曲线。答案: 。
(差的绝对值)平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于|F1F2|,且不等于0)的点的轨迹叫做双曲线。这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距。通常情况下,我们把|F1F2|记为2c(c>0); 常数记为2a(a>0).问题2:
定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?问题1:定义中为什么强调距离差的绝对值为常数?一、双曲线的定义①若2a=2c,则轨迹是什么?②若2a>2c,则轨迹是什么?③若2a=0,则轨迹是什么?此时轨迹为以F1或F2为端点的两条射线此时轨迹不存在此时轨迹为线段F1F2的垂直平分线F1F2F1F2分3种情况来看:二、双曲线标准方程的推导① 建系使 轴经过两焦点 , 轴为线段 的垂直平分线。② 设点设 是双曲线上任一点, 焦距为 ,那么 焦点 又设|MF1|与|MF2| 的差的绝对值等于常数 。③ 列式即将上述方程化为: 移项两边平方后整理得: 两边再平方后整理得: 由双曲线定义知: 即:设 代入上式整理得: 两边同时除以 得:④化简这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在x轴上,焦点是 F1(-c,0),F2(c,0).其中c2=a2+b2.类比椭圆的标准方程,请思考焦点在y轴上的双曲线的标准方程是什么?其中c2=a2+b2.这个方程叫做双曲线的标准方程 ,它所表示的双曲线的焦点在y轴上,焦点是 F1(0,-c),F2(0,c).三.双曲线两种标准方程的比较① 方程用“-”号连接。② 分母是 但 大小不定。③ 。 ④如果 的系数是正的,则焦点在 轴上;如果 的系数是正的,则焦点在 轴上。F(±c,0)F(±c,0)a>0,b>0,但a不一定大于b,c2=a2+b2a>b>0,a2=b2+c2四、双曲线与椭圆之间的区别与联系||MF1|-|MF2||=2a |MF1|+|MF2|=2a F(0,±c)F(0,±c)例题解:因为双曲线的焦点在x轴上,所以设它的标准方程为因此,双曲线的标准方程为方法总结:
求标准方程要做到先定型,后定量。两条射线轨迹不存在例1、已知双曲线的焦点 F1(-5,0), F2(5,0),双曲线上一点P到焦点的距离差的绝对值等于8,求双曲线的标准方程。1.若|PF1|-|PF2|=8呢?2.若||PF1|-|PF2||=10呢?3.若||PF1|-|PF2||=12呢?所以2c=10,2a=8。即a=4,c=5那么b2=c2-a2=25-16=9根据已知条件,|F1F2|=10. ||PF1|-|PF2||=8,归纳小结双曲线的定义双曲线的标准方程布置作业
54页习题2.2 A组1、2题。谢谢!题后反思(1)先把非标准方程化成标准方程,再判断焦点所在的坐标轴。(2) 是否表示双曲线? 表示焦点在 轴上的双曲线;表示焦点在 轴上的双曲线。答案: 。
