2018年高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质课件4新人教B版选修2_1(14张)
文档属性
| 名称 | 2018年高中数学第二章圆锥曲线与方程2.3.2双曲线的几何性质课件4新人教B版选修2_1(14张) |  | |
| 格式 | zip | ||
| 文件大小 | 442.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:31:55 | ||
图片预览


文档简介
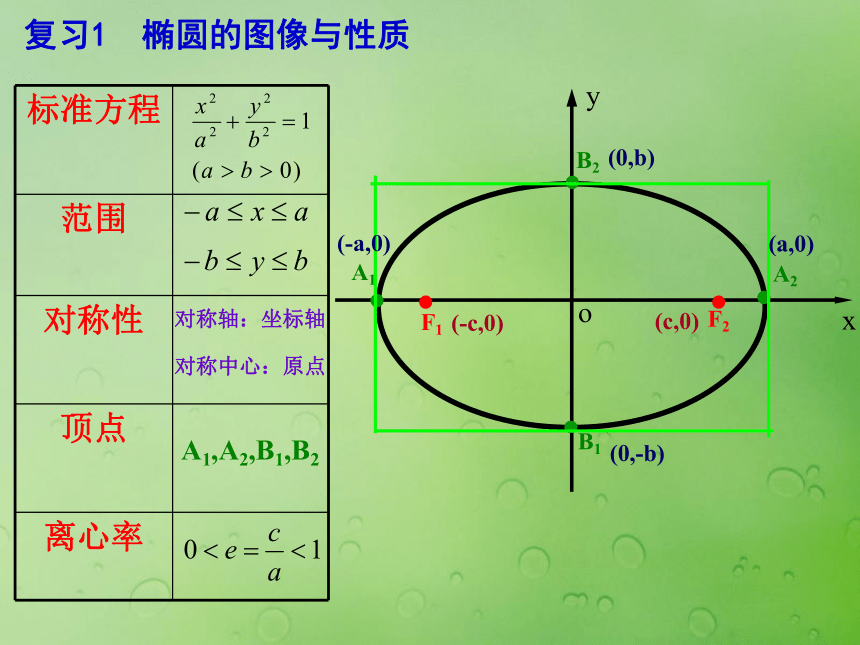
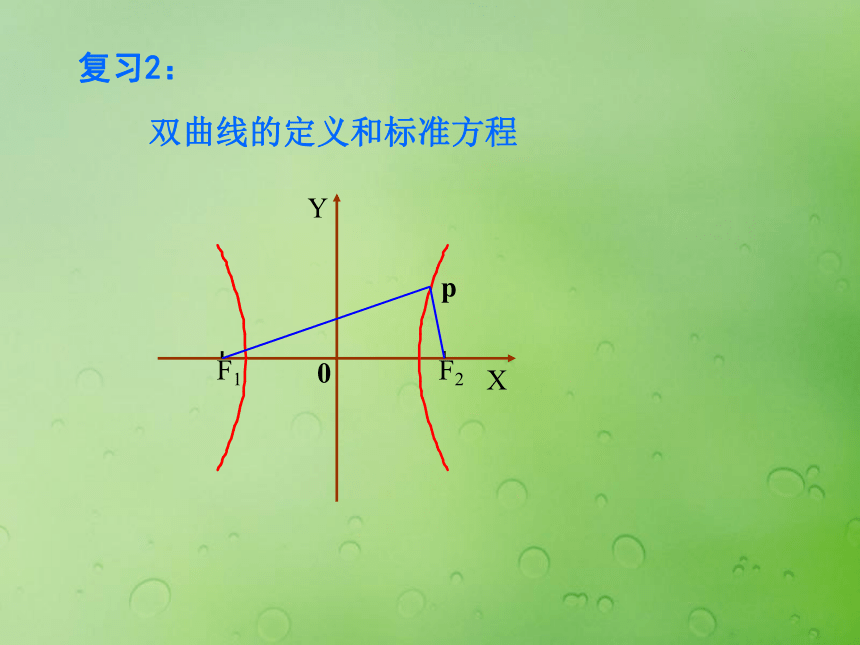
课件14张PPT。oyxA1A2B2B1复习1 椭圆的图像与性质对称轴:坐标轴对称中心:原点A1,A2,B1,B2(-a,0)(a,0)(0,-b)(0,b)复习2:双曲线的定义和标准方程 2、对称性 一、研究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都对称.x轴、y轴是双曲线的对称轴,原点是对称中心,
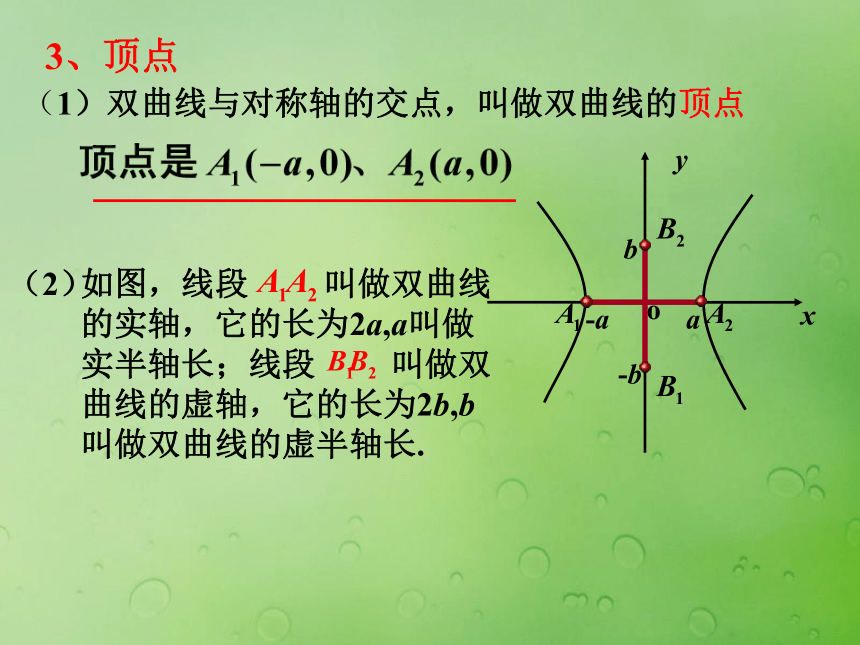
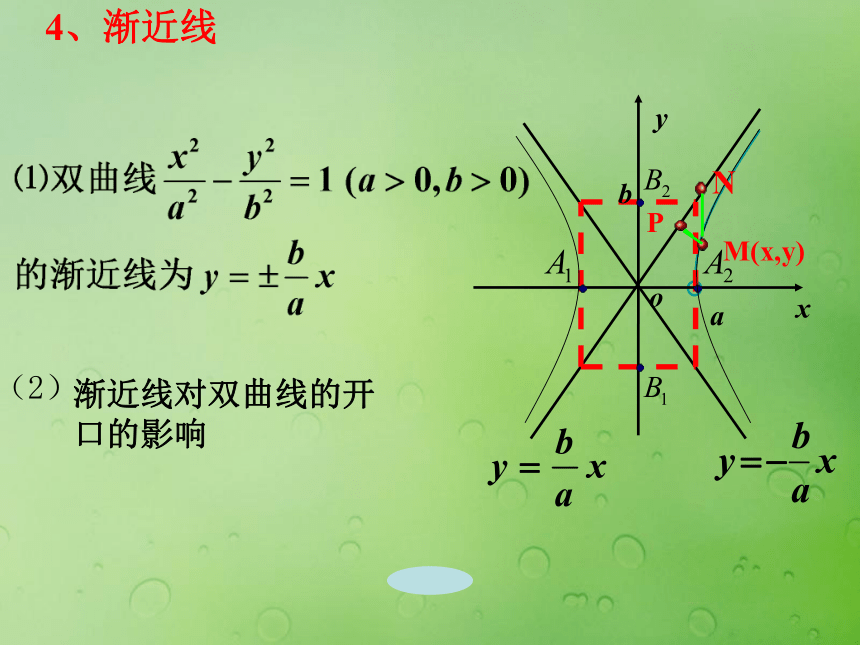
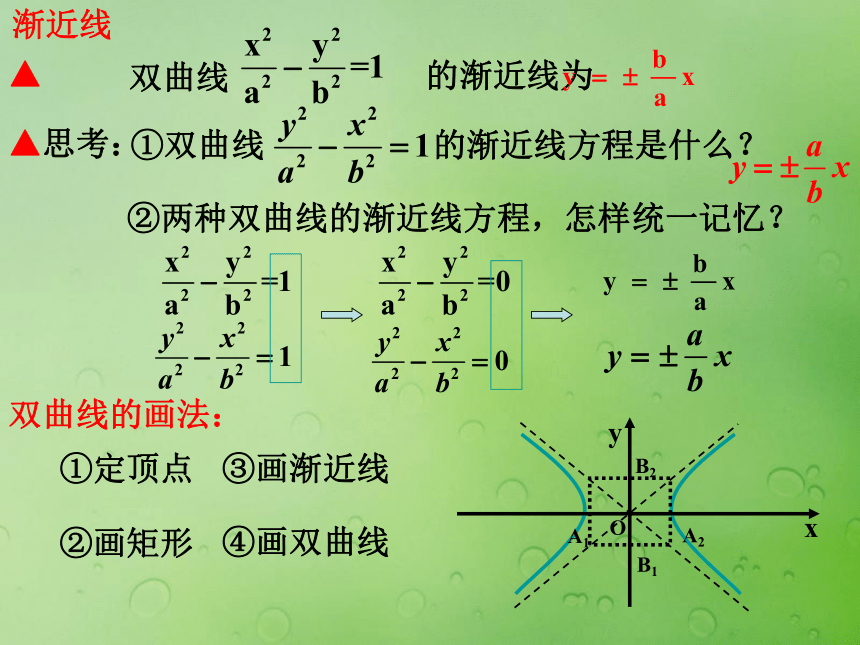
又叫做双曲线的中心.(-x,-y)(-x,y)(x,y)(x,-y)3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点4、渐近线渐近线对双曲线的开口的影响(2)M(x,y)▲思考:▲ 渐近线②两种双曲线的渐近线方程,怎样统一记忆? 的渐近线为双曲线①双曲线 的渐近线方程是什么? 双曲线的画法:①定顶点②画矩形③画渐近线④画双曲线5、离心率e是表示双曲线开口大小的一个量,e 越大开口越大(动画演示)c>a>0e >1(±a , 0 )(±c , 0 )( 0, ±a )( 0, ±c )x 轴、y 轴、原点( 原点是双曲线的中心 )| x | ≥ a| y | ≥ a 【例1】已知求双曲线的焦点在x轴上,中心在原点,如果焦距为8,实轴长6,求双曲线的标准方程和离心率.热点探究一:由双曲线的几何性质求其方程变式训练:已知双曲线一焦点坐标为(5,0),一渐近线方程为3x-4y=0,求此双曲线的标准方程和离心率.【例2】求双曲线 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.热点探究二:由双曲线的方程研究其几何性质变式训练:在例2中,如果把双曲线的方程换为 呢?课堂小结:
通过本节课的学习,
你有哪些收获?ab关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)B1(0,-b),B2(0,b)F1(-c,0) F2(c,0)关于x轴、y轴、原点对称A1(- a,0),A2(a,0)实轴长2a,虚轴长2b椭圆的几何性质双曲线的几何性质 类比祝同学们学习进步
又叫做双曲线的中心.(-x,-y)(-x,y)(x,y)(x,-y)3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点4、渐近线渐近线对双曲线的开口的影响(2)M(x,y)▲思考:▲ 渐近线②两种双曲线的渐近线方程,怎样统一记忆? 的渐近线为双曲线①双曲线 的渐近线方程是什么? 双曲线的画法:①定顶点②画矩形③画渐近线④画双曲线5、离心率e是表示双曲线开口大小的一个量,e 越大开口越大(动画演示)c>a>0e >1(±a , 0 )(±c , 0 )( 0, ±a )( 0, ±c )x 轴、y 轴、原点( 原点是双曲线的中心 )| x | ≥ a| y | ≥ a 【例1】已知求双曲线的焦点在x轴上,中心在原点,如果焦距为8,实轴长6,求双曲线的标准方程和离心率.热点探究一:由双曲线的几何性质求其方程变式训练:已知双曲线一焦点坐标为(5,0),一渐近线方程为3x-4y=0,求此双曲线的标准方程和离心率.【例2】求双曲线 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.热点探究二:由双曲线的方程研究其几何性质变式训练:在例2中,如果把双曲线的方程换为 呢?课堂小结:
通过本节课的学习,
你有哪些收获?ab关于x轴、y轴、原点对称图形方程范围对称性顶点离心率A1(- a,0),A2(a,0)B1(0,-b),B2(0,b)F1(-c,0) F2(c,0)关于x轴、y轴、原点对称A1(- a,0),A2(a,0)实轴长2a,虚轴长2b椭圆的几何性质双曲线的几何性质 类比祝同学们学习进步
