2018年高中数学第三章空间向量与立体几何3.1.3两个向量的数量积课件2新人教B版选修2_1(23张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.1.3两个向量的数量积课件2新人教B版选修2_1(23张) |  | |
| 格式 | zip | ||
| 文件大小 | 843.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:36:06 | ||
图片预览








文档简介
课件23张PPT。两个向量的数量积教学过程几个概念
1、 两个向量的夹角的定义夹
角
的
顶
点
为
两
个
向
量
的
起
点
空间 (1)异面直线的定义
的两条直线叫做异面直线.
(2)两条异面直线所成的角
把异面直线 ,这时两条直线的夹角( )叫做两条异面直线所成的角.如果所成的角是直角,则称两条异面直线 .不同在任何一平面内平移到一个平面内锐角或直角互相垂直2、异面直线所成的角的范围:(0°,90°]
3、两个向量的数量积注意:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
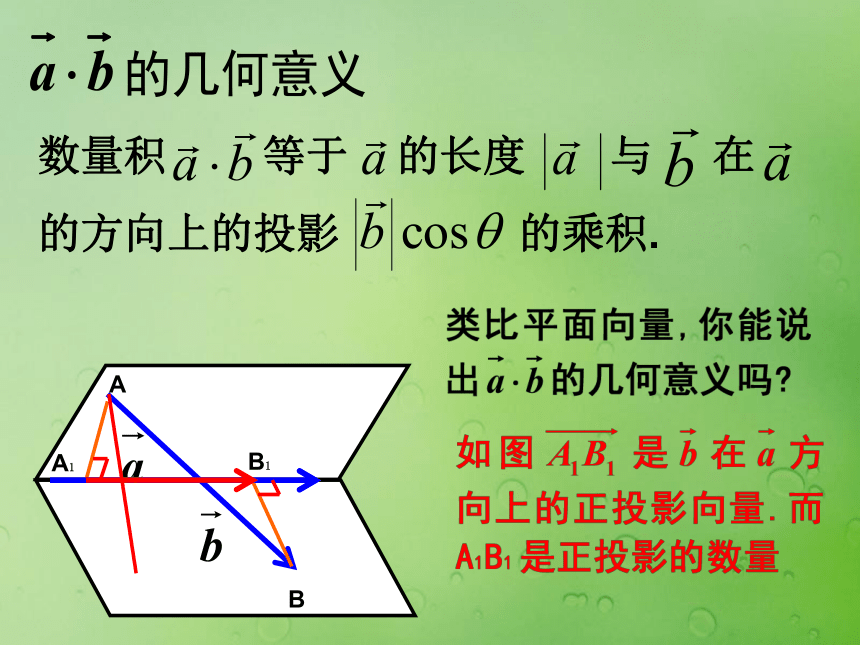
A1B1BA数量积 等于 的长度 与 在
的方向上的投影 的乘积.不一定为锐角不一定为钝角练习: 空间向量的数量积性质 注意:①性质2)是证明两向量垂直的依据;
②性质3)是求向量的长度(模)的依据;
(3)性质4是求两个向量夹角的依据;对于非零向量 ,有:空间向量数量积的运算律 向量数量积的运算适合乘法结合律吗?
即(a?b)c=a(b·c)吗?注意:1、数量积不满足结合律即?2、数量积不能约分3、向量没有除法?
向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立。课堂练习③提示:1.下图中异面直线AB与C'A'的夹角多大?同
的夹角有什么关系?依据是什么?
的夹角呢?合作学习一 异面直线所成的角结论:异面直线的夹角与它们上面两个向量的夹角有什么关系?相等或互补互补相等2.已知平面α⊥平面β,
点A,B在 内,并且它们在 上的正射影分别为A',B';
点C,D在 内,并且它们在 上的正射影分别为C',D',
求证: 合作学习二 两个向量的数量积1.已知正四面体ABCD的每条棱长都等于a,点E,F,G分别是棱AB,AD,DC的中点,求下列向量的数量积:
知识迁移 数量积的应用解:数量积的应用(一)求线段长度和两点距离数量积的应用(二)证垂直例3. 如图所示,在正方体ABCD-A1B1C1D1中,
求异面直线BA1与AC所成的角. 数量积的应用(三) 求角[解题感悟]
求异面直线所成的角的关键是求异面直线上两向量的数量积,而要求两向量的数量积,必须把所求向量用空间的一组基向量来表示.空间向量数量积的定义空间向量数量积的性质空间向量数量积的运用空间向量的夹角小结谢谢指导
1、 两个向量的夹角的定义夹
角
的
顶
点
为
两
个
向
量
的
起
点
空间 (1)异面直线的定义
的两条直线叫做异面直线.
(2)两条异面直线所成的角
把异面直线 ,这时两条直线的夹角( )叫做两条异面直线所成的角.如果所成的角是直角,则称两条异面直线 .不同在任何一平面内平移到一个平面内锐角或直角互相垂直2、异面直线所成的角的范围:(0°,90°]
3、两个向量的数量积注意:
①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于零。
A1B1BA数量积 等于 的长度 与 在
的方向上的投影 的乘积.不一定为锐角不一定为钝角练习: 空间向量的数量积性质 注意:①性质2)是证明两向量垂直的依据;
②性质3)是求向量的长度(模)的依据;
(3)性质4是求两个向量夹角的依据;对于非零向量 ,有:空间向量数量积的运算律 向量数量积的运算适合乘法结合律吗?
即(a?b)c=a(b·c)吗?注意:1、数量积不满足结合律即?2、数量积不能约分3、向量没有除法?
向量的数量积运算类似于多项式运算,平方差公式、完全平方公式、十字相乘等均成立。课堂练习③提示:1.下图中异面直线AB与C'A'的夹角多大?同
的夹角有什么关系?依据是什么?
的夹角呢?合作学习一 异面直线所成的角结论:异面直线的夹角与它们上面两个向量的夹角有什么关系?相等或互补互补相等2.已知平面α⊥平面β,
点A,B在 内,并且它们在 上的正射影分别为A',B';
点C,D在 内,并且它们在 上的正射影分别为C',D',
求证: 合作学习二 两个向量的数量积1.已知正四面体ABCD的每条棱长都等于a,点E,F,G分别是棱AB,AD,DC的中点,求下列向量的数量积:
知识迁移 数量积的应用解:数量积的应用(一)求线段长度和两点距离数量积的应用(二)证垂直例3. 如图所示,在正方体ABCD-A1B1C1D1中,
求异面直线BA1与AC所成的角. 数量积的应用(三) 求角[解题感悟]
求异面直线所成的角的关键是求异面直线上两向量的数量积,而要求两向量的数量积,必须把所求向量用空间的一组基向量来表示.空间向量数量积的定义空间向量数量积的性质空间向量数量积的运用空间向量的夹角小结谢谢指导
