2018年高中数学第三章空间向量与立体几何3.2.3直线与平面的夹角课件2新人教B版选修2_1(20张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2.3直线与平面的夹角课件2新人教B版选修2_1(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 576.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:37:59 | ||
图片预览




文档简介
课件20张PPT。直线与平面夹角2学习目标123 理解平面和夹角的定义,体会夹角定义的唯
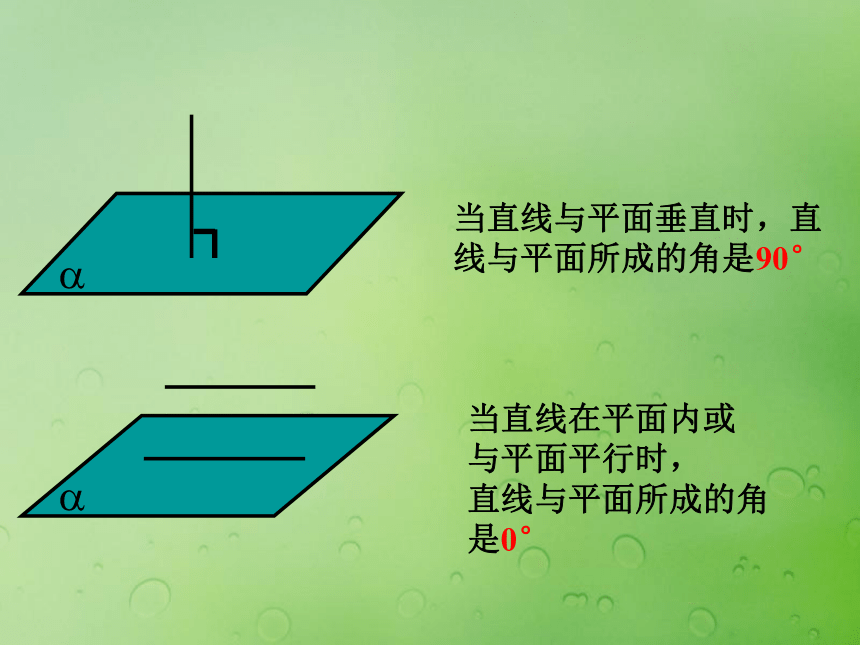
一性,合理性 探究如何用向量方法求直线与平面之间的夹角,获得求直线与平面之间夹角的方法认识事物之间的规律性,进一步体会向量方法在立体几何中的具体作用。当直线与平面垂直时,直
线与平面所成的角是90°当直线在平面内或
与平面平行时,
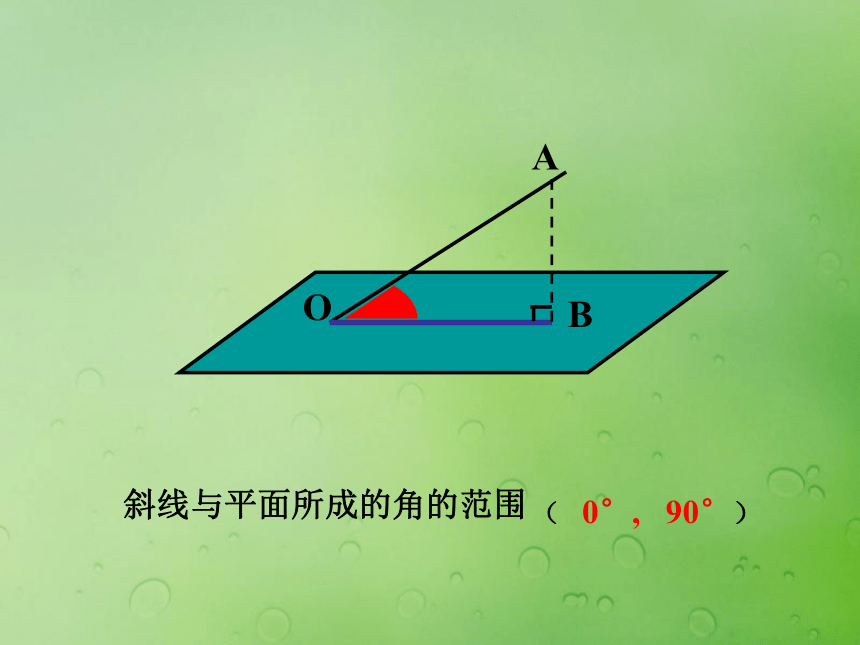
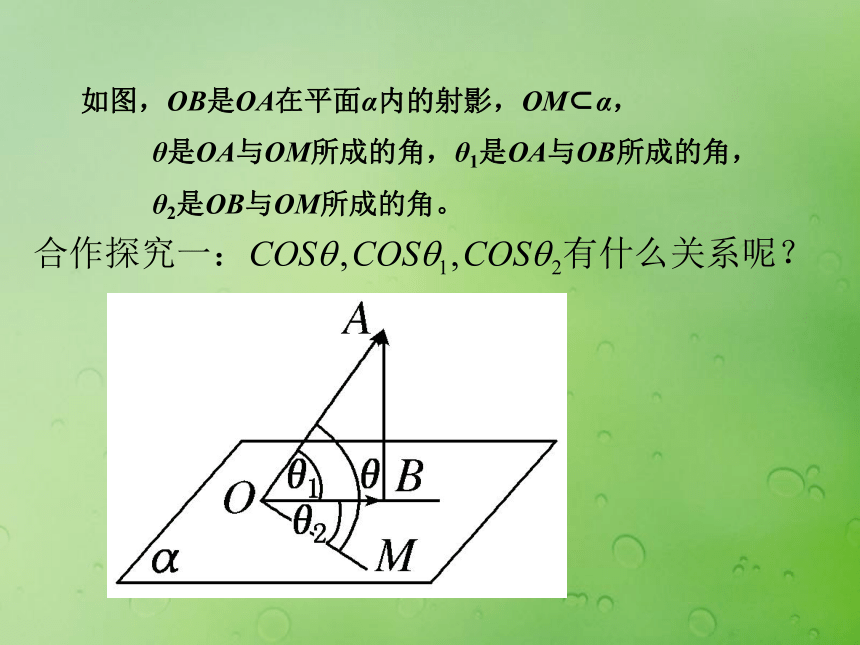
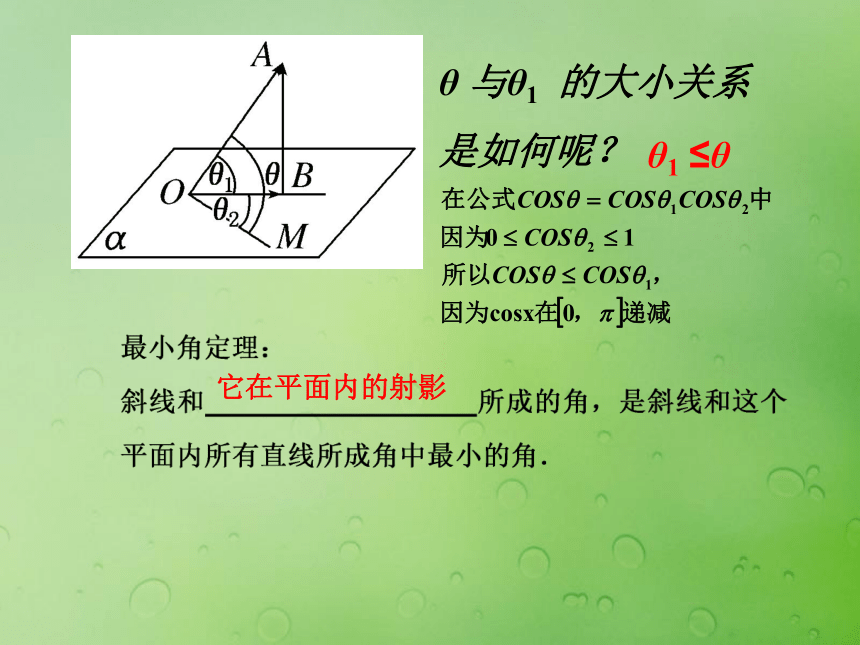
直线与平面所成的角是0°( 0°, 90°)斜线与平面所成的角的范围 如图,OB是OA在平面α内的射影,OM?α,
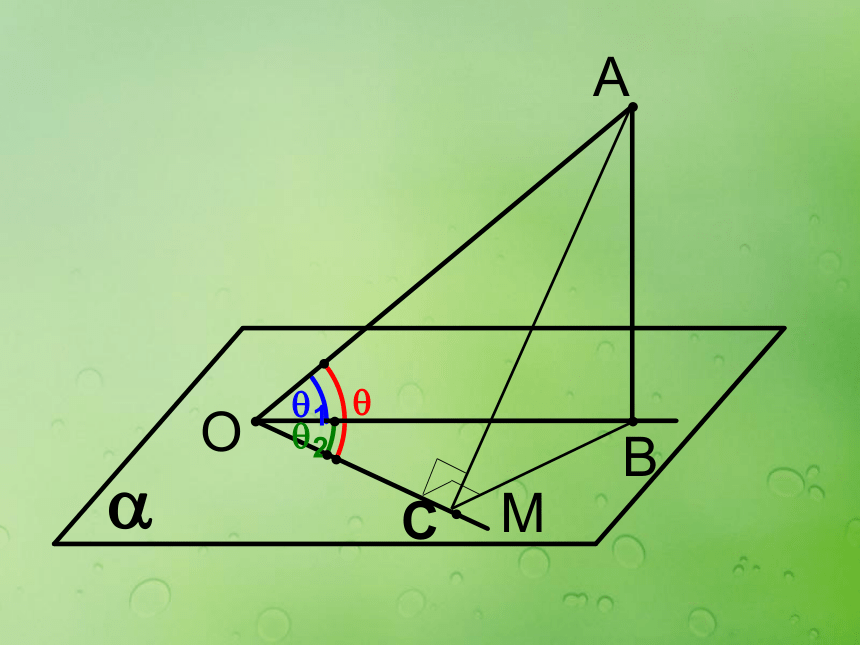
θ是OA与OM所成的角,θ1是OA与OB所成的角,
θ2是OB与OM所成的角。Cθ 与θ1 的大小关系
是如何呢?它在平面内的射影θ1 ≤θ二、线面角的求法:定义法的具体步骤如下:
①找过斜线上一点与平面垂直的直线;1.定义法 ②连结垂足和斜足,得出斜线在平面的 射影,确定出所求的角;
③把该角置于三角形中计算。例题探究:
如图,在四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC ┴ 底面ABCD。已知 AB=SB=SC= 2
求直线SA与平面ABCD所成角SABCD取BC中点O,连接SO,AOSDSADSBADSSDSADSC思考:合作探究结论:二、向量法:直线与平面所成角: 例题研究:
xyz设正方体棱长为1,以A坐标原点,分别AB,AD,AA所在直线为x,y,z轴建立如图所示的空间坐标系小结这节课你学到了什么? 在正方体ABCD—A1B1C1D1中(如图),
M、N分别是棱B1C1、AD的中点,求
直线AD与平面BMD1N所成角的余弦值.
祝同学们学习进步!
一性,合理性 探究如何用向量方法求直线与平面之间的夹角,获得求直线与平面之间夹角的方法认识事物之间的规律性,进一步体会向量方法在立体几何中的具体作用。当直线与平面垂直时,直
线与平面所成的角是90°当直线在平面内或
与平面平行时,
直线与平面所成的角是0°( 0°, 90°)斜线与平面所成的角的范围 如图,OB是OA在平面α内的射影,OM?α,
θ是OA与OM所成的角,θ1是OA与OB所成的角,
θ2是OB与OM所成的角。Cθ 与θ1 的大小关系
是如何呢?它在平面内的射影θ1 ≤θ二、线面角的求法:定义法的具体步骤如下:
①找过斜线上一点与平面垂直的直线;1.定义法 ②连结垂足和斜足,得出斜线在平面的 射影,确定出所求的角;
③把该角置于三角形中计算。例题探究:
如图,在四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC ┴ 底面ABCD。已知 AB=SB=SC= 2
求直线SA与平面ABCD所成角SABCD取BC中点O,连接SO,AOSDSADSBADSSDSADSC思考:合作探究结论:二、向量法:直线与平面所成角: 例题研究:
xyz设正方体棱长为1,以A坐标原点,分别AB,AD,AA所在直线为x,y,z轴建立如图所示的空间坐标系小结这节课你学到了什么? 在正方体ABCD—A1B1C1D1中(如图),
M、N分别是棱B1C1、AD的中点,求
直线AD与平面BMD1N所成角的余弦值.
祝同学们学习进步!
