2018年高中数学第三章空间向量与立体几何3.2.4二面角及其度量课件2新人教B版选修2_1(17张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2.4二面角及其度量课件2新人教B版选修2_1(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 621.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 22:38:56 | ||
图片预览






文档简介
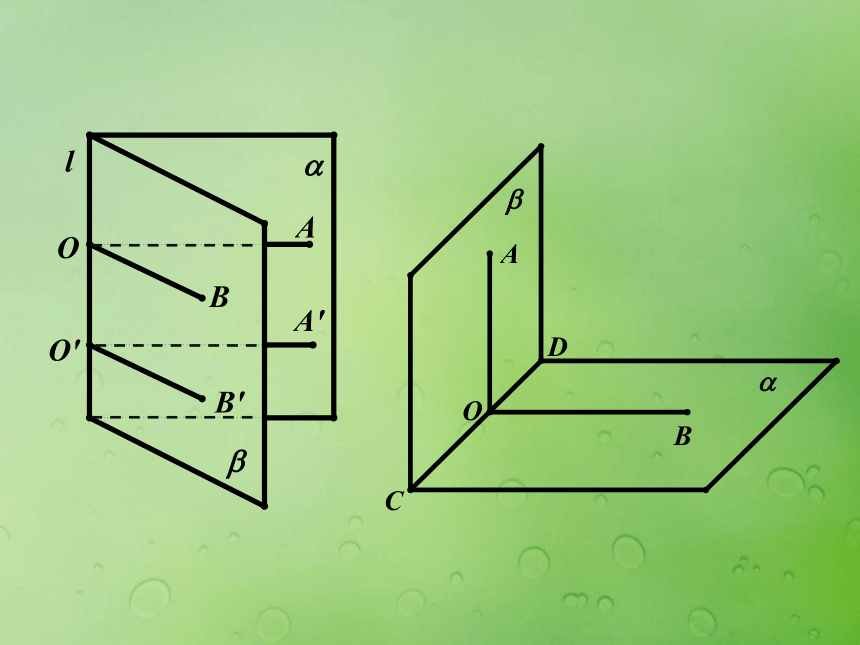
课件17张PPT。3.2.4 二面角及其度量 平面内一条直线把平面分成两部分,其中的每一部分都叫做半平面,从一条直线出发的两个半平面所组成的图形叫做二面角;这条直线叫做二面角的棱,每个半平面叫做二面角的面。棱为l,两个面分别为α,β的二面角,记作α-l-β,二面角也可以记作A-l-B。 在二面角α-l-β的棱上任取一点O,在两个半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角α-l-β的平面角,显然,这个平面角与点O在l上的位置无关.
二面角的大小可以用它的平面角来度量,二面角的平面角是几度,就说这个二面角是几度。我国发射的第一颗人造卫星的倾斜角是68.5°,这个倾斜角指的人造卫星的轨道平面与地球的赤道平面所成的角。 本书中,我们约定,二面角不小于0°,不大于180°。
即0 °≤ θ ≤180°
平面角是直角的二面角叫做直二面角,互相垂直的平面也就是相交成直二面角的两个平面。 我们可以用向量的夹角来研究二面角的性质及其度量。例1.如图,在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm, AC=6cm,BD=8cm,CD= cm,求这个二面角的度数。例2.已知:二面角α-l-β的度数为θ (0≤θ≤ ),在α面内有△ABC,它在β内的射影为△A’BC,它们的面积分别为S,S’,求证:S’=Scosθ.证明:不妨假定△ABC的边BC在l上,
作BC边的高AD,AD在β内的射影为A’D,
根据正射影的性质,知A’D=ADcosθ,
S’=BC×A’D
=BC×ADcosθ
=Scosθ.例3.已知ABCD是直角梯形,∠DAB= ∠ABC=90°,SA⊥平面ABCD,SA=AB= BC=1,AD= ,求平面SAB与SCD的夹角的正切。解2:画出二面角的平面角:例4.已知E, F分别是正方体ABCD-A1B1 C1D1的棱BC和CD的中点,求:
(1)A1D与EF所成角的大小;
(2)A1F与平面B1EB所成角的大小;
(3)二面角C-D1B1-B的大小。60°(2)A1F与平面B1EB所成角的大小;
(3)二面角C-D1B1-B的大小。
二面角的大小可以用它的平面角来度量,二面角的平面角是几度,就说这个二面角是几度。我国发射的第一颗人造卫星的倾斜角是68.5°,这个倾斜角指的人造卫星的轨道平面与地球的赤道平面所成的角。 本书中,我们约定,二面角不小于0°,不大于180°。
即0 °≤ θ ≤180°
平面角是直角的二面角叫做直二面角,互相垂直的平面也就是相交成直二面角的两个平面。 我们可以用向量的夹角来研究二面角的性质及其度量。例1.如图,在一个二面角的棱上有两个点A,B,线段AC,BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm, AC=6cm,BD=8cm,CD= cm,求这个二面角的度数。例2.已知:二面角α-l-β的度数为θ (0≤θ≤ ),在α面内有△ABC,它在β内的射影为△A’BC,它们的面积分别为S,S’,求证:S’=Scosθ.证明:不妨假定△ABC的边BC在l上,
作BC边的高AD,AD在β内的射影为A’D,
根据正射影的性质,知A’D=ADcosθ,
S’=BC×A’D
=BC×ADcosθ
=Scosθ.例3.已知ABCD是直角梯形,∠DAB= ∠ABC=90°,SA⊥平面ABCD,SA=AB= BC=1,AD= ,求平面SAB与SCD的夹角的正切。解2:画出二面角的平面角:例4.已知E, F分别是正方体ABCD-A1B1 C1D1的棱BC和CD的中点,求:
(1)A1D与EF所成角的大小;
(2)A1F与平面B1EB所成角的大小;
(3)二面角C-D1B1-B的大小。60°(2)A1F与平面B1EB所成角的大小;
(3)二面角C-D1B1-B的大小。
