2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件2新人教B版选修2_1(15张)
文档属性
| 名称 | 2018年高中数学第三章空间向量与立体几何3.2空间向量在立体几何中的应用课件2新人教B版选修2_1(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 478.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-11-24 00:00:00 | ||
图片预览



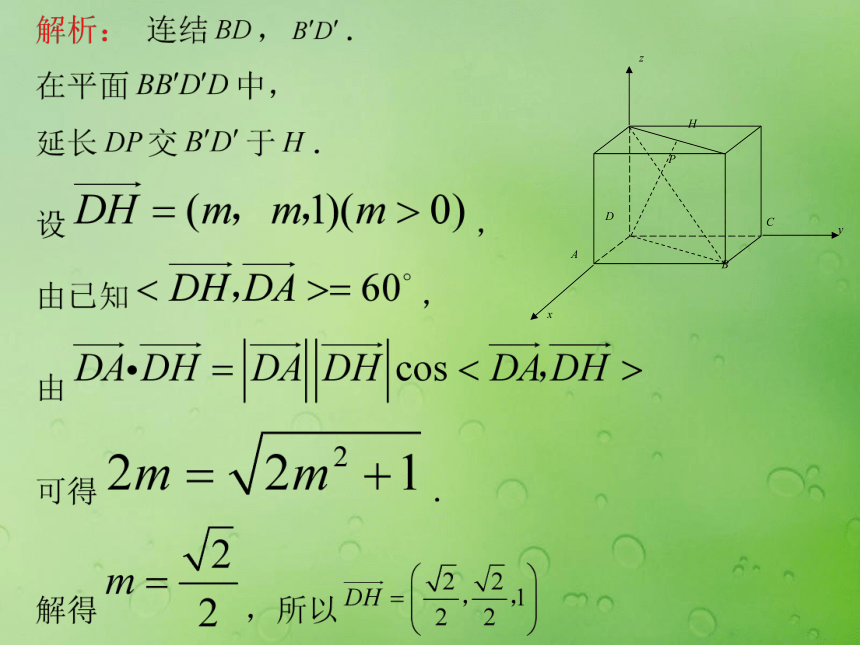

文档简介
课件15张PPT。 用向量方法求
空间中的角例1: 如图所示,在棱长为1的正方体ABCD—A1B1C1D1中,(1)求异面直线BA1和AC所成的角.(2)求直线AB和面ACD1所成的角
(3)求面BA1B1和
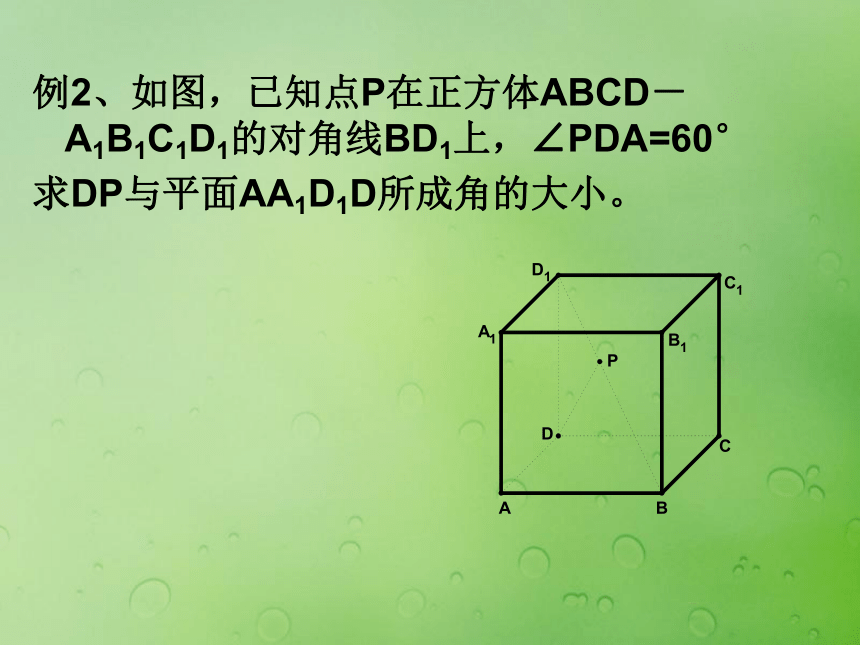
面ACD1所成的锐角例2、如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°
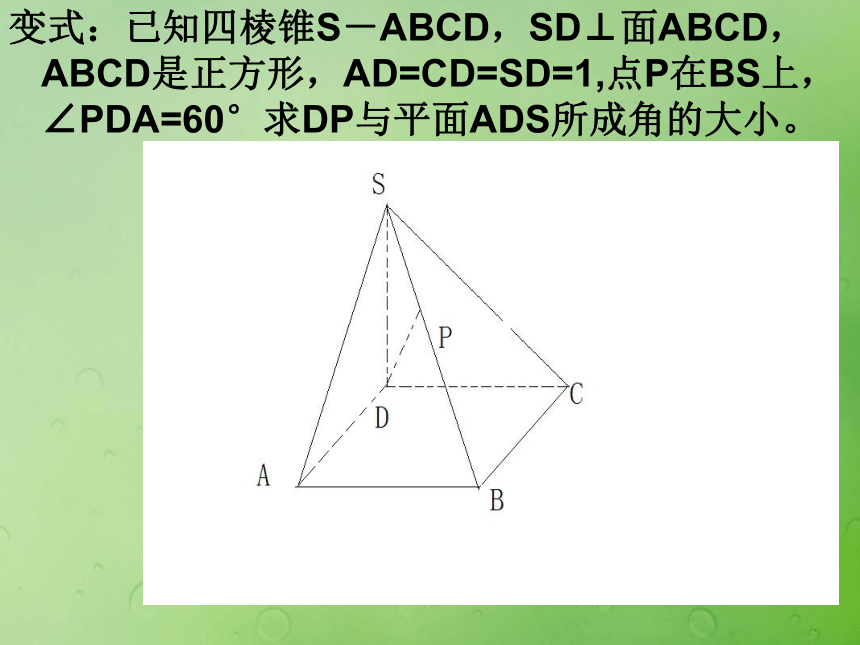
求DP与平面AA1D1D所成角的大小。例2、如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°求DP与平面AA1D1D所成角的大小。D1A1变式:已知四棱锥S-ABCD,SD⊥面ABCD, ABCD是正方形,AD=CD=SD=1,点P在BS上,∠PDA=60°求DP与平面ADS所成角的大小。设两条异面直线所成角θ,求这两条直线的方向向量先分别求出二面角的两个半平面所在平面的法向量,再求两法向量夹角余弦值。判断出所求二面角的平面角是锐角还是钝角,确定出二面角的平面角的大小.
空间中的角例1: 如图所示,在棱长为1的正方体ABCD—A1B1C1D1中,(1)求异面直线BA1和AC所成的角.(2)求直线AB和面ACD1所成的角
(3)求面BA1B1和
面ACD1所成的锐角例2、如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°
求DP与平面AA1D1D所成角的大小。例2、如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°求DP与平面AA1D1D所成角的大小。D1A1变式:已知四棱锥S-ABCD,SD⊥面ABCD, ABCD是正方形,AD=CD=SD=1,点P在BS上,∠PDA=60°求DP与平面ADS所成角的大小。设两条异面直线所成角θ,求这两条直线的方向向量先分别求出二面角的两个半平面所在平面的法向量,再求两法向量夹角余弦值。判断出所求二面角的平面角是锐角还是钝角,确定出二面角的平面角的大小.
